My Version of Pascal's Triangle
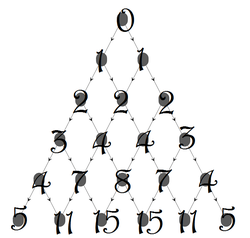 The above picture shows the first six rows of my version of Pascal's Triangle. The basic rules apply, but the first and last term for all
n
th
equals to
n
−
1
.
The above picture shows the first six rows of my version of Pascal's Triangle. The basic rules apply, but the first and last term for all
n
th
equals to
n
−
1
.
Let f ( n ) denote the sum of the entries in the row that begins with n .
What is the value of f ( 5 0 ) f ( 1 0 0 ) m o d 2 5 ?
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Fantastic!
Nice problem but overrated!
f ( 0 ) = 0 , f ( 1 ) = 2 , f ( 2 ) = 6 , f ( 3 ) = 1 4 ⇒ f ( n ) = 2 ( 2 n − 1 ) Now we assume this is true and use induction. Well it is clear to see that each element in a row except for the ends is counted twice to obtain the next row. This means we have to over-count, subtract the elements at the end and then add the ends of the next row as follows: f ( n + 1 ) = 2 f ( n ) − 2 n + 2 ( n + 1 ) = 4 ( 2 n − 1 ) + 2 = 2 n + 2 − 2 = 2 ( 2 n + 1 − 1 ) a s r e q u i r e d SO: f ( 5 0 ) f ( 1 0 0 ) = 2 ( 2 5 0 − 1 ) 2 ( 2 1 0 0 − 1 ) = 2 5 0 − 1 ( 2 5 0 + 1 ) ( 2 5 0 − 1 ) = 2 5 0 + 1 2 1 0 ≡ − 1 m o d ( 2 5 ) ∴ 2 5 0 + 1 ≡ − 1 + 1 ≡ 0 m o d ( 2 5 )
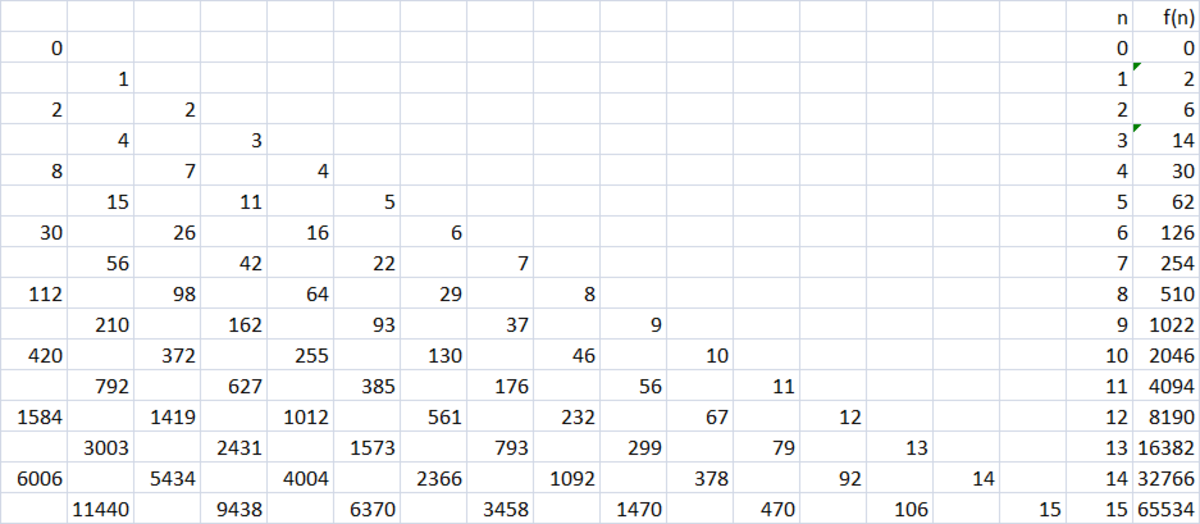
By observation and induction it can be shown that (see this special Pascal Triangle above):
f ( n ) = 2 n + 1 − 2
Therefore,
f ( 5 0 ) f ( 1 0 0 ) = 2 5 1 − 2 2 1 0 1 − 2 = 2 5 0 − 1 2 1 0 0 − 1 = 2 5 0 − 1 ( 2 5 0 + 1 ) ( 2 5 0 − 1 ) = 2 5 0 + 1
Now it is to find:
( 2 5 0 + 1 ) ( m o d 2 5 ) ≡ [ ( 2 1 0 ) 5 + 1 ] ( m o d 2 5 )
≡ [ ( 1 0 2 5 − 1 ) 5 + 1 ] ( m o d 2 5 ) ≡ ( − 1 + 1 ) ( m o d 2 5 ) ≡ 0 ( m o d 2 5 )
Exactly the way I did it, I'm not sure why this problem is so difficult. Congrats @Parth Lohomi for such a cool pattern! :D
Log in to reply
Yes, I very nice problem.
Thanks sir!!
Pascal triangle which i Knew is not same as here.. I thought pascal triangle is like this . The pattern of numbers doesn't match ..
Log in to reply
You are right. This is another triangle for this problem only. It is just like a pascal but not it
Log in to reply
can you please tell me the pattern of number in nth row...
Log in to reply
@Vighnesh Raut – I can but it is very tedious. There is a pattern. You know that the first element of each row is n , the second element is 2 , 4 ( 2 + 2 ) , 7 ( 4 + 3 ) , . . . and all that.
Log in to reply
@Chew-Seong Cheong – thnx......the elements are obtained same as obtained in real pascal's triangle...
Log in to reply
@Vighnesh Raut – Yes, that is why the title of the problem is "Inspired by Pascal Triangle". It is not Pascal Triangle but works like one.
am i the only on who use intitution?
Let { n p } the element in the n -th row and p -th column. So { n 0 } = { n p } = n and the "Pascal Rule" holds: { n p } + { n p + 1 } = { n + 1 p + 1 } Then, we have: f ( n ) = p = 0 ∑ n { n p } ⇒ 2 f ( n ) = { n 0 } + p = 0 ∑ n − 1 [ { n p } + { n p + 1 } ] + { n n } ⇒ 2 f ( n ) + 2 = p = 0 ∑ n + 1 { n + 1 p + 1 } ⇒ f ( n + 1 ) = 2 f ( n ) + 2 Notice that f ( 0 ) = 0 . Then: k = 1 ∑ n 2 k − 1 f ( k ) = k = 1 ∑ n 2 k − 2 f ( k − 1 ) + 2 k − 2 1 ⇒ f ( n ) = 2 n + 1 − 2
So, f ( 5 0 ) f ( 1 0 0 ) = 2 5 1 − 2 2 1 0 1 − 2 = 2 5 0 + 1 . Notice that 2 1 0 = 1 0 2 4 ≡ − 1 m o d 2 5 ⇒ 2 5 0 + 1 ≡ 0 m o d 2 5 So, the answer is 0