Inspired by Pranjal Jain
What is the value of
∫ − 1 1 x 1 d x ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Discussions for this problem are now closed
What if we apply kings property of integration..? I got the answer "0"..
Can you explain what the "kings property of integration" is? This is my first time hearing about it, and a google search did not turn up anything useful.
Please clearly state all conditions under which the property holds, paying special attention to what happens about vertical asymptotes.
King Rule is nothing but a property of definite integrals that (integral of f(x) from a to b is same as integral of f(a+b-x) from a to b)
@Prakash Chandra Rai – Do you mean that "King Rule" is the property of definite integrals that ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x ?
@Prakash Chandra Rai – If that's the case, then we are saying that "does not exist = does not exist", and so there is no contradiction.
Generally for such theorems, they assume first that the integral exists (and is finite) as a condition. E.g. even saying that ∫ f + g = ∫ f + ∫ g assumes that both of these integrals are finite, because we do not have arithmetic on infinity.
@Calvin Lin – If we consider the original question and after applying the king property and adding both.. It will be integral of 1/x + integral of-1/x...The sum is zero.
@Mohanish Gaikwad – No, what you have is "does not exist + does not exist", which is equal to "does not exist".
The king property does not guarantee existence / finiteness of the integral. It assumes existence / finiteness.
Note: We do not have (complete) arithmetic operation on the reals + infinity. We cannot conclude that 0 = ∞ − ∞ .
It is exactly as said by prakash rai.
Doesn't x 1 simply integrate to Ln x , which becomes undefined because a n > 0 (for real a and n). In other words, we can't have Ln(-1)
Not quite. Usually, the way to deal with a negative denominator, is to take absolute values.
For example, we can integrate ∫ − 1 k x 1 d x = [ − ln ∣ x ∣ ] − 1 k for any − 1 < k < 0 .
So it means that the integral ∫ a b f ( x ) d x does not exist if there exist a point c in the interval [ a , b ] such that f ( c ) is not defined......please correct me if i am wrong
@Aman Sharma – There are exceptions. Say you have a function with a point of discontinuity, say f ( x ) = x − 1 x 2 − 1 . This function is undefined at x = 1 , but since
lim x → 1 f ( x ) = 2 ,
we find that, for example,
∫ 0 2 f ( x ) = 4 .
I think that your statement may be accurate when asymptotes are involved, although I'd have to do a bit of research to be certain of this.
@Brian Charlesworth – I am quite curious to know ,how you will modify this statement sir
@Aman Sharma – See the explanation given below by me.
@Aman Sharma – No, that statement is not true. The value of an integral can be defined even though there are points which are undefined. For example, we can show that ∫ 0 1 x 1 d x = 2 , even though 0 1 isn't defined.
Isn't integral ( 1/x) = ln(|x|) ?
Actually, Integrate d x/ x ought to be Ln (x) + C XOR Ln (-x) + C some more!
As d (Ln x)/ d x = 1/ x and d [Ln (-x)]/ d x = 1/ x while d x/ x = d (-x)/ (-x).
Not crossing x = 0, it is easy to say as Ln | x | because Ln (-1) = j Pi hasn't been known. Since only difference of same side is to be evaluated at once, the sign is added to avoid doubt only. What we obtain as a result of integration is not everything but something that shall tell the value of integral from one domain to another domain.
isn't it ln (-1)=pi(i)?
Absolutely. Although it can't be graphed on an x y plane
There is a method, though, of assigning a value, (known as the Cauchy principal value ), to an improper integral such as this. In this case the value would be 0 . (I was mildly concerned that this was the value you had in mind; I always get a bit nervous when it comes to multiple-choice questions. :))
P.S.. I can't seem to attach links anymore when making comments to solutions. Is there a trick to doing this?
Let me test that: Community .
You should be able to link using the markdown syntax of
[title](URL Link)
O.k., thanks for testing that. I did the usual thing, starting with [Cauchy principal value](, and then tried to bring a copy of the link down into place, only to have the copy just disappear. It's been doing that for a few days when trying to post links in comments, so I just thought I'd ask if the method had changed. I can still type out the address, (as I have now done in my edited initial comment), and have the link posted, but this is not ideal as some addresses are prohibitively long. Anyway, the problem would seem to be at my end, then, so I'll now try to figure out the cause of the glitch. Thanks again.
P.P.S.. The question you've linked to has been deleted. I'm curious as to what it was.
@Brian Charlesworth – It was ∫ 3 π 0 ( tan x ) ( tan 2 x ) ( tan 3 x ) .
Sorry I deleted it knowing that it does not converge!
@Calvin Lin If you want to link that question, add it again with an edit like "Answer 1729 if it does not exist".
I really don't know much about calculus and my answer's probably stupid, but can you explain why you can't just do: 1:-1 ∫ x^(-1) = [0x^0] = 0
Can you please tell me then what is the value of integral 0 to pi secx dx.
the integral diverges as we tend to pi/2. See my explanation given below in 2nd answer.
How do we get around the problem of undefined integrand for x = 0 ? I'd say that the integral is actually lim t → 0 ∫ − 1 − t t 1 + ∫ t 1 t 1 , not lim t → 0 ∫ − 1 − t t 1 + lim t → 0 ∫ t 1 t 1 .
Note that your limits should not be the same variable as the function that you are integrating. ∫ t 1 t 1 d x = ∫ t 1 x 1 d x . In particular, t cannot be both a constant and a variable (esp for clarity of expression).
The first integral that you stated, where we remove an interval of equal radius about 0, is also known as the Cauchy Principle value. It requires us to make the assumption that one rate of change is dependent on the other (in fact, equal). This is not typical, especially when dealing with functions in many variables.
For example, when we consider 2 sided limits for derivative by first principles, we do not require to take
lim
h
→
0
2
h
f
(
a
+
h
)
−
f
(
a
−
h
)
, but instead require the wider collection of
lim
h
→
0
,
j
→
0
h
+
j
f
(
a
+
h
)
−
f
(
a
−
j
)
.
If we took the first interpretation, then
∣
x
∣
is differentiable at 0, with a derivative of 0. However, this is not what we would have expected. This highlights the danger of making the perturbations dependent on each other.
The function x 1 has a discontinuity at x = 0 ; it decreases without bound as we approach 0 from the left and increases without bound as we approach 0 from the right. Thus, we have to split up the integral at the discontinuity and use limits to evaluate:
∫ − 1 1 x 1 d x = a → 0 − lim ∫ − 1 a x 1 d x + b → 0 + lim ∫ b 1 x 1 d x
The antiderivative of x 1 is ln ∣ x ∣ :
= a → 0 − lim ln ∣ x ∣ ∣ ∣ ∣ − 1 a + b → 0 + lim ln ∣ x ∣ ∣ ∣ ∣ b 1 = a → 0 − lim ( ln ( − a ) − ln 1 ) + b → 0 + lim ( ln 1 − ln b ) = a → 0 − lim ln ( − a ) − b → 0 + lim ln b
Since these limits don't exist, the integral can't be evaluated.
Note: It is best to use distinct variables.
One might be tempted at the end to say that
a → 0 − lim ln ( − a ) − a → 0 + lim ln a = a → 0 lim ( ln a − ln a )
Instead, it is best to use the variable a for the first, and b for the second.
Thanks! I've edited my solution accordingly.
This is explanation of the answer given by #Calvin Lin
Fundamental theorem of calculus says that differentiation is reverse process for integration only for the functions which are continuous in the interval. Since 1/x is discontinuous at x=0 , we can't integrate it using Fundamental Theorem of Calculus.
Now, we have to go to basics to find the answer.
If we divide the interval in infinitesimal rectangles, we have to see the area bounded by the rectangle as x approaches 0.
If we can neglect that area bounded by that rectangle, we can simply use Fundamental Theorem of calculus. (Reason: If we can neglect area bounded if x tends to 0, we can remove the point 0 from our domain, and if we remove point from our domain, we can use fundamental theorem of calculus).
A simple way to do this is to first to integrate it within the given limit without caring about any rule. If answer is finite, then only we can neglect that area. If the answer is infinite, then we can't neglect the area bounded by that rectangle. And if we can neglect the area bounded by that curve, we can use fundamental theorem of Calculus.
Reason why we can neglect the area when answer is finite:
If you know basics about convergent and divergent series, then it is easier to observe why we can do so. If we remove some terms from a convergent series, then the new generated series is also convergent and summation of a convergent series is always finite (more precisely,when number of terms will tend to infinity, then it will approach a finite limit).
Interestingly, if number of terms are infinite, then it doesn't matter how many finite terms you neglect, you will get the same answer. There are many more interesting properties of convergent and divergent series. I will post a question regarding this.
While if the series is divergent, Then it's summation will be infinite(more precisely,when number of terms will tend to infinity, then it will approach a infinite limit). Example of a divergent series is summation of terms in Harmonic Progression. Some Divergent series can be changed to convergent series by removing some finite terms. So, we can't neglect any term in a divergent series.
Here, we have removed the area bounded by the rectangle when x approaches 0. Here we have applied Fundamental Theorem of calculus, and got a infinite answer, then we can simply state that the initial series was divergent and if above series was divergent, we can't neglect the area bounded by that interval. And also,we can conclude nothing about area bounded by the rectangle as x approaches infinity. Hence, the integral doesn't exists.
Great answer.
Another way to understand it, is that when we try and take ∫ − 1 − ϵ 1 x 1 d x + ∫ ϵ 2 1 x 1 d x
then the convergence of these integrals depend on the values of ϵ 1 , ϵ 2 . If we took ϵ 1 = ϵ 2 (EG Cauchy Principal value), then these integrals cancel out and the limit exists. However, we were to say take ϵ 2 = 2 ϵ 1 , then the sum tends to negative infinity. As such, the limit does not exist, which is why the integral does not exist.
More easy but Advanced Method, I don't know much about Cauchy Principal Value. But after all, It is small and nice method.
So why does ∫ − 1 1 x 3 1 d x converge to 0?
My apologies. It does not converge either, for the same reason.
I have fixed the integral and changed it to ∫ − 1 1 ∣ x ∣ . 5 s g n ( x ) d x .
Thanks for clearing my concepts
You're Welcome
The way I look at it, x 1 has a discontinuity at zero, hence integrating on [ − 1 , 1 ] doesn't make sense, so it gets rewritten as two separate integrals: lim a → 0 − ∫ − 1 a x 1 d x + lim b → 0 + ∫ b 1 x 1 d x = ( ( ln ( 0 − ) − ln ( − 1 ) ) + ( ln ( 1 ) − ln ( 0 + ) ) ) = − ∞ + ∞ Which doesn't exist.
it is obvious that the integral of 1/x w.r.t x is lnx whose asymptote is y=0, bt the interval is from -1 to 1 or twice the range from 0 to 1 and fortunately this does help us because we will have 2[ln1-ln0]=2ln1-2ln0=0-2ln0=-2ln0. the question is, what power of e will give zero? i can safely say the power should be of form -x for some pstive x so that e^-x will approach zero for some pstive x, the good news is it will not be zero, yep thus right. and so x must approach infinity and in turn, our desired results:it does not exist
Not really.
Note that if we are integrating over the negative numbers, then ∫ x 1 d x = ln ∣ x ∣ As such, when you integrate ∫ − 1 0 x 1 d x , what you will "get" is ln 0 − ln 1 (where i am using your logic). If so, this gives us ln 1 − ln 0 + ln 0 − ln 1 = 0 , instead of − 2 ln 0 .
Your logic of "no value of x works" is not valid. For example, ∫ − 1 1 x 3 1 d x = 0 , even though there is no value of x such that 0 = x 2 − 2 .
I think that this integral is also not defined i.e. it is divergent.
Without any intuition as to the properties of the asymptotes on the curve y = 1/x, by simply integrating we reach the solution: ln(1) - ln(-1) We know that the natural log of 1 is 0 but the natural log of any negative number is undefined. Hence we cannot assign a value in this case.
Simply, integrating 1/x gives us lnx So the definite integral equals ln1 - ln(-1) Since ln-1 cannot be defined, the answer is does not exist
Not quite.
The definite integral is only defined for x > 0 . We have:
For x > 0 , ∫ x 1 d x = ln x + C .
It does not include the case of x < 0 . To deal with the indefinite integral on the region x < 0 , we have
For x < 0 , ∫ x 1 d x = ln ∣ x ∣ + C .
The issue comes about when we want to integrate "across" 0, which we are not allowed to do.
Isn't area under a curve supposed to be the same as the result of definite integral? Also, I don't quite remember/understand why the parts don't cancel out when the graph is symmetric? It's been 5 years since I have solved anything math related, so I feel like a noob again... :) Also, could you give me a link to some place where I can maybe read more about this? Thanks!
Not quite. It is the same when the integral is well defined (and finite). In this case, because the integral is not well defined, this interpretation is not valid.
Essentially, what this integral is saying, is that we cannot evaluate ∞ − ∞ as an arithmetic operation. We cannot say that the value is 0, or 1, or anything else.
In another sense, "parts cancel out as this graph is symmetric" is essentially saying that 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + … is equal to 0. This expression is also not well defined. (If it has to be assigned a value, it would be 2 1 by cesaro summation.)
@Calvin Lin – Thanks for the explanation Calvin... :)
@Calvin Lin – Ah, the good 'ol Grandi's series! :)
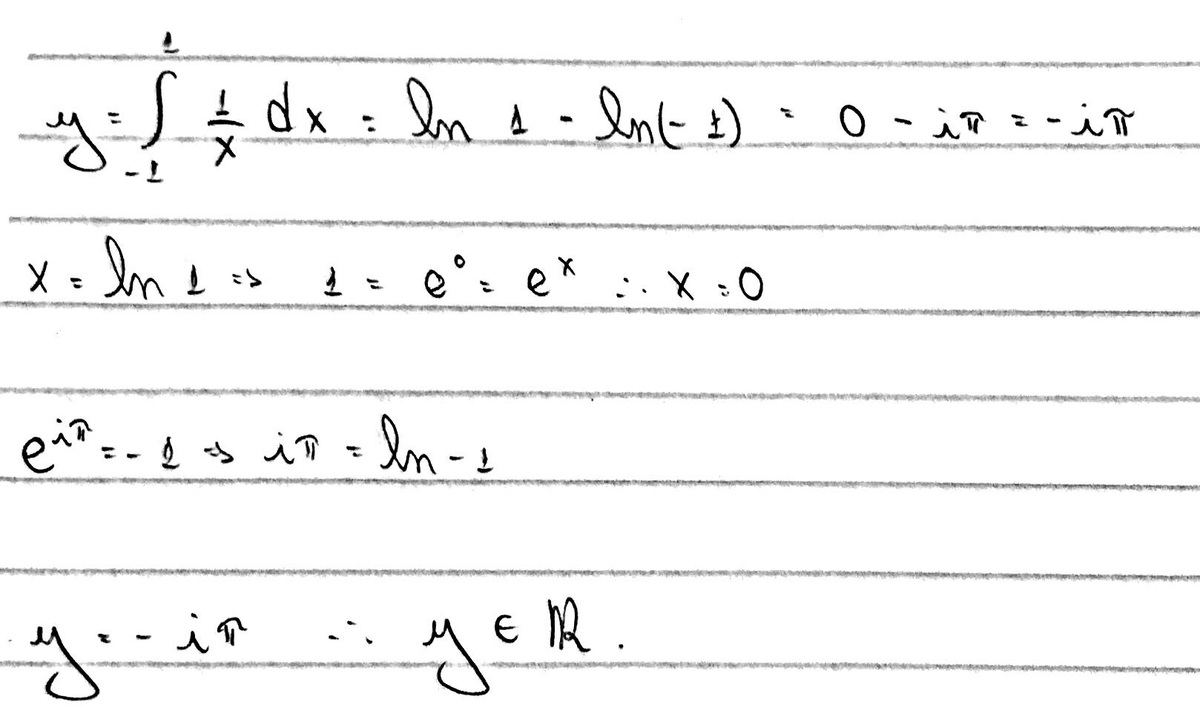
The integral does not converge.
When integrating over a vertical asymptote, we have to be very careful that the integral converges absolutely. We cannot simply say "the graphs are symmetric hence the parts must cancel out".
In this case, because ∫ − 1 1 ∣ ∣ x 1 ∣ ∣ d x is not finite, hence the integral in the question is undefined.
Note: ∫ − 1 1 x 1 / 2 s g n ( x ) d x = 0 .