Inspired by Rajen Kapur
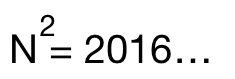
What is the smallest perfect square whose first four digits is 2016?
Note: Give the value of the perfect square.
The answer is 20164.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Those who only try 2 0 1 6 ≈ 4 4 . 8 9 … will get a different answer.
Log in to reply
I thought maybe I wasn't reading the question correctly. "First four digits is 2016", so since 2016 is not a perfect square, try a 5 digit number starting with 2016. Still, I did try a different approach for the more general problem. No need to go into details here now.
Log in to reply
Yup, there is a very nice approach for the general problem, and we can also find a bound of the number of values to try.
Log in to reply
Log in to reply
@Harsh Shrivastava – Think about how to approach the problem in a sensible way, and in particular why we seem to care about n and such.
If you're stuck, check out this problem .
See expanded comments above. Is that what you're looking for?
I chosed to use a Javascript algorithm for this:
function findSmallestPerfectSquare() {
var i = 1;
while (true) {
var tmp = i*i;
if (tmp.toString().substring(0,4) === "2016") {
return tmp;
} else {
i++;
}
}
}
var smallestPerfSquare = findSmallestPerfectSquare();
console.log(smallestPerfSquare);
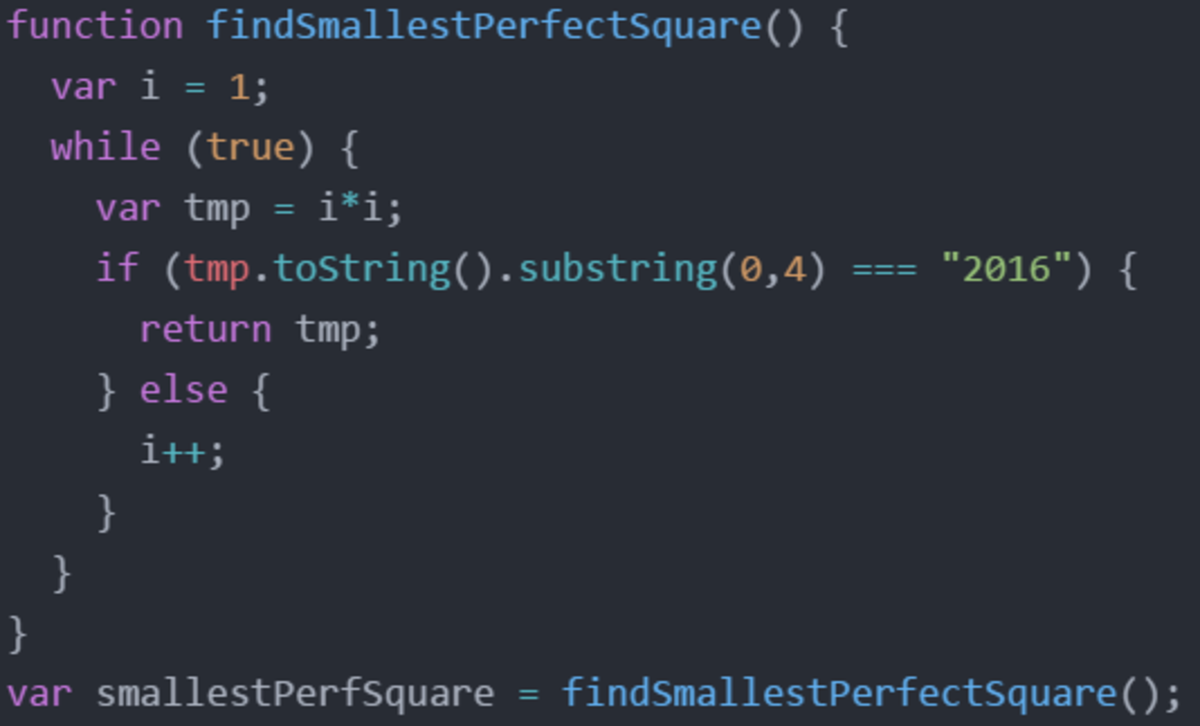
Which will generate perfect squares and then check if the perfect squares' first 4 numbers is 2016. If not proceed to next perfect square. Returns: 20164 after 10ms (not fast I know)
What are various ways that we can speed up the program?
Log in to reply
The mayor time issue is converting it to string and checking, but I don't know of any other method...
Other than that we could start with a higher number for example 44 which is the closest number under 2016. One could also check 44*44 manually and see that it has to be above 44 and check what sqrt(20160) (which is the next possible answer after 2016) and start with that number
I would love some suggestions to making it faster guys!
Log in to reply
Sometimes, understanding the underlying mathematical structure can provide a simple approach :)
well, a square of anumber has in its unit place a
-
1 if the the number has 1 in its unit place. but
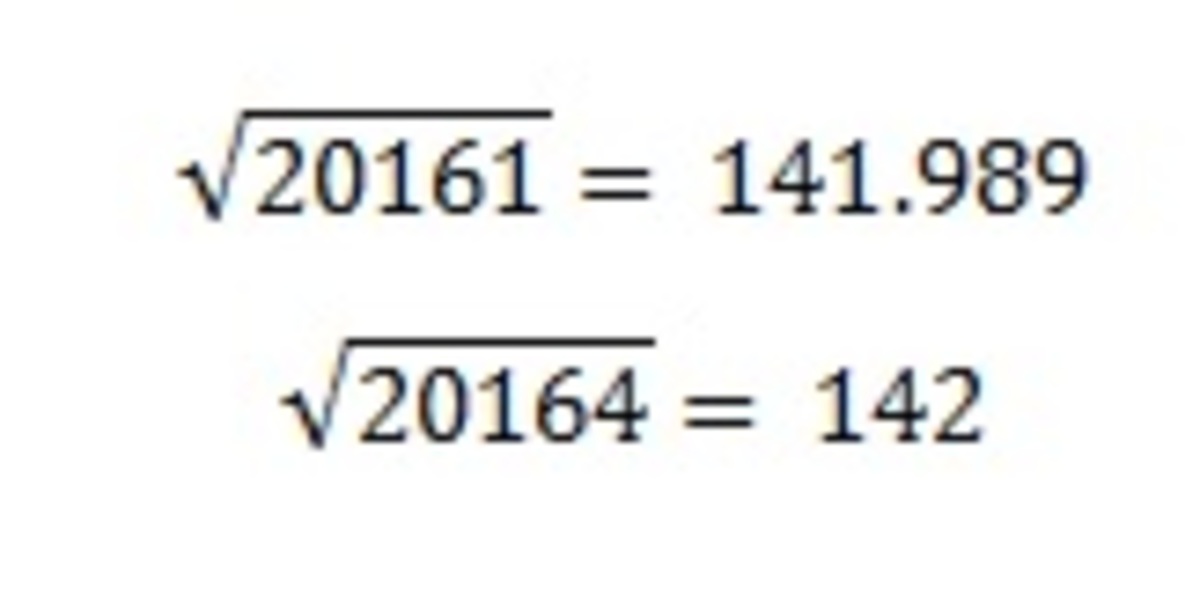
-
4 if the number has 2 in its unit place. Thus, 20164 is the number.
How would you deal with the general case?
Log in to reply
Sir, In general it will be the same. The unit digit is always between (0-9) for a particular number and for them we always have
1 in unit place of square for numbers with 1 in unit place
4 in unit place of square for numbers with 2 in unit place
9 in unit place of square for numbers with 3 in unit place
6 in unit place of square for numbers with 4 in unit place
5 in unit place of square for numbers with 5 in unit place
and so on till 9
and for square numbers if: n*n= {n}^{2}
and for square of (n+1) will be [{n}^{2}+ 2*n+1]
i.e. for eg., n=2, then square =4 and next number square = 4+2n+1=9, which the square of 3
Log in to reply
Say that the number we want the square to start off with is 3999.
Are you going to test 39990, 39991, 399994, 39999, 399901, 399904, 399904, etc?
Log in to reply
@Calvin Lin – Yes sir, I will start by testing the unit digit, because only they will be the square numbers, but there is no need to test all of them, simply by checking one number, we can get an oversight of the number we want to find.
@Calvin Lin – Sir,Could you please post a note on how to solve this? I too thought what Abhay said was the only approach
Is there a theoretical way to do this?
?.... um... 2 0 1 6 0 = 1 4 1 . 9 8 6 , so try 1 4 2 2 = 2 0 1 6 4 ?
All right, this problem has generated numerous comments. Let's generalize a bit. Consider a number 2 0 1 6 followed by a digits. Then we examine, for each a , how many n can there be. n has to satisfy the following
2 0 1 6 ⋅ 1 0 a < n < 2 0 1 7 ⋅ 1 0 a
which can be rewritten as
2 0 1 6 < n ⋅ 1 0 − 2 1 a < 2 0 1 7
or
4 4 . 8 9 9 . . . < n ⋅ 1 0 − 2 1 a < 4 4 . 9 1 1 . . .
which means for a square of an even number of digits starting with digits 2 0 1 6 , the unique answer is always 4 4 9 followed by zeroes. Likewise, the first expression can be rewritten as
( 2 0 1 6 ⋅ 1 0 < n ⋅ 1 0 − 2 1 ( a − 1 ) < 2 0 1 7 ⋅ 1 0 )
or
1 4 1 . 9 8 6 . . . < n ⋅ 1 0 − 2 1 ( a − 1 ) < 1 4 2 . 0 2 1 . . .
which means for a square of an odd number of digits starting with 2 0 1 6 , the unique answer is always 1 4 2 followed by zeroes. See the following to see the uniqueness of 1 4 2 and 4 4 9
2 0 1 6 4 = 1 4 2 2
2 0 1 6 0 1 = 4 4 9 2
2 0 1 6 4 0 0 = 1 4 2 0 2
2 0 1 6 0 1 0 0 = 4 4 9 0 2