Inspired by Rama Devi
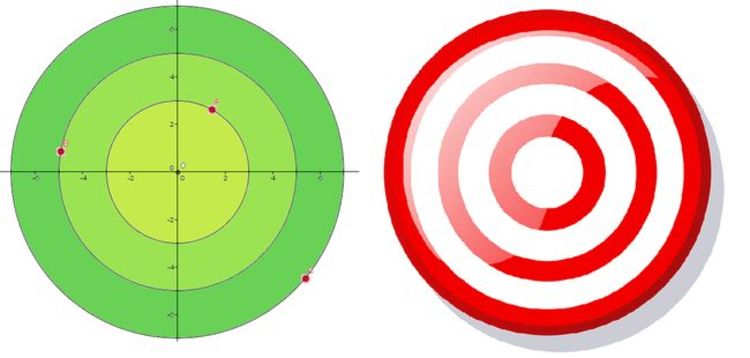 There are 3 concentric circles with center
O
and radii
3
,
5
,
7
units. Points
A
,
B
,
C
are respectively on these circles, one on each circle.
There are 3 concentric circles with center
O
and radii
3
,
5
,
7
units. Points
A
,
B
,
C
are respectively on these circles, one on each circle.
When A B 2 + B C 2 + C A 2 is maximized, what is the value of sin ∠ A O B (to 3 decimal places)?
The answer is 0.866.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
What is the simple geometric condition for a + b + c = 0 ?
Great solution, leaving it in vector form.
I was trying to deal with the more general case, but got stuck (and didn't recognize) the scenario of a + b + c = 0 .
In the scenario where c > a + b , I believe that the maximum occurs when they 3 points lie on a line, with O between C and AB.
Log in to reply
a + b + c = 0 implies that the orthocenter coincides with the circumcenter, which means that △ A B C is necessarily equilateral (or degenerate)
Log in to reply
I fail to see how you came to that conclusion. I think that you are confused with the incorrect work that you had been doing in your solution.
a + b + c = 0 means that when the vectors are lined up, they form a closed loop. IE a triangle. This explains why when we are calculating the angle between a and b , we're simply doing a "cosine rule on 3-5-7 triangle".
Thus for triangle ABC to exist (as in the solution) <=> a + b + c = 0 <=> the lengths of vectors satisfies the triangle inequality. Hence, I talk about the remaining case when the triangle doesn't exist, which is if a + b > c (or cyclic permutation).
Log in to reply
@Calvin Lin – Ah, I thought he set O as the origin. My bad.
Log in to reply
@Nathan Ramesh – O is the origin. a = O A . He mentioned that a + b + c = 0 implies that "centroid = origin".
Maybe your confusion is from thinking that O is also the circumcenter?
Log in to reply
@Calvin Lin – Yeah. Whoops usually O is the circumcenter.
This solution was once correct, when the problem was misworded.
Here is how to get the right answer.
Notice how it is never given which point is on which circle, so the answer must be the same in all cases. Hence sin ∠ A O B = sin ∠ B O C = sin ∠ C O A , where ∠ A O B + ∠ B O C + ∠ C O A = 2 π . It is not that hard to conclude this only happens when all angles are equal to 1 2 0 ∘ which gives an answer of 2 3 . Thanks Calvin :)
Moderator note:
This solution is completely incorrect. He was lucky in guessing the numerical answer, but it is not backed by mathematical rigor.
Fixed the problem.
FYI your claim that the angles are equal is wrong.
Log in to reply
Oh, rats. I guess you're right, but the only other way it can happen is with 3 collinear points.
I just tried to actually solve the problem but something is not working out. I circumvented the use of calculus and just used complex numbers instead, letting A = 3 a , B = 5 b , C = 7 c , for a , b , c on the unit circle. Hence A B 2 = ∣ 5 b − 3 a ∣ 2 = ( 5 b − 3 a ) ( 5 b − 3 a ) = ( 5 b − 3 a ) ( b 5 − a 3 ) = 3 4 − 1 5 ( b a + a b ) = 3 4 − 3 0 ℜ ( b a ) , and similarly for the other sides. After doing the other terms and simplifying, and WLOG setting a = 1 , it suffices to minimize 1 5 ℜ ( b ) + 2 1 ℜ ( c ) + 3 5 ℜ ( c b ) However, from b c = 1 , we get b = c 1 hence we want to minimize 3 6 ℜ ( b ) + 3 5 ℜ ( b 2 ) Letting ℜ ( b ) = cos x ⟹ ℜ ( b 2 ) = cos 2 x = 2 cos 2 x − 1 , we want to minimize 7 0 cos 2 x + 3 6 cos x − 3 5 , which doesn't happen when cos x = − 2 1 ...?
Please let me know if you see a mistake anywhere @Calvin Lin
Log in to reply
Why is
b
c
=
1
? They are any 2 complex numbers on the unit circle.
We have
∣
b
c
∣
=
1
, but that doesn't really help.
Up to that, you're on the right track. Converting the complex numbers in angles, we want to minimize
1
5
cos
β
+
2
1
cos
γ
+
3
5
cos
(
β
−
γ
)
.
Log in to reply
@Calvin Lin – Thanks @Calvin Lin
Although the b c = 1 thing was wrong, shouldn't it still give an expression that is minimized when cos x = − 2 1 ?
Log in to reply
@Nathan Ramesh – Why? The expression after that is wrong.
IE 1 5 R ( b ) + 2 1 R ( c ) = 3 6 R ( b ) and 3 5 R ( b / c ) = 3 5 R ( b 2 ) .
I do not see how you can eliminate c at all.
Log in to reply
@Calvin Lin – Assuming b c = 1 , the minimum should occur when cos x = − 1 / 2 , but it doesn't, unless I did something else wrong...?
Log in to reply
@Nathan Ramesh – The minimum of 7 0 cos 2 x + 3 6 cos x − 3 5 occurs at cos x = − 2 × 7 0 3 6 .
Why should it happen at cos x = − 2 1 ? You are solving a different question, why should the solution be identical to this question?
(Either that, or I'm really confused by what you mean).
Log in to reply
@Calvin Lin – The minimal case should be the minimal case in all subsets of cases, and for the subset such that b c = 1 , there is a different minimal case, unless I am doing something wrong. @Calvin Lin
@Calvin Lin – Got till the last expression, but not getting how to minimise it
Log in to reply
@Appan Rakaraddi – Use Calculus. This problem is placed under Calculus after all.
Log in to reply
@Calvin Lin – The problem seems so nice that we shouldn't need calculus to solve it. The fact that O is the Fermat point of ABC (probably) has some nice connection to it. (The Fermat point being the point in △ A B C such that ∠ A O B = ∠ B O C = ∠ C O A = 1 2 0 ∘ , is also well known to minimize A O + B O + C O .)
Log in to reply
@Nathan Ramesh – No, O is not the Fermat point of ABC. Only ∠ A O B = 1 2 0 ∘ . The rest of the angles are different.
For all such triangles, we have O A + O B + O C = 3 + 5 + 7 . Just because O is the point that minimizes the vertex sum for this particular triangle, doesn't have significant bearing on A B 2 + B C 2 + C A 2 over all possible triangles with O A = 3 , O B = 5 , O C = 7 .
No, even with the miswording, this solution is not at all correct. As mentioned, the angles are not equal.
Let a = O A , b = O B , c = O C . Then ∣ a ∣ = 3 , ∣ b ∣ = 5 , ∣ c ∣ = 7 , and
A B 2 + A C 2 + B C 2 = ∣ a − b ∣ 2 + ∣ a − c ∣ 2 + ∣ b − c ∣ 2 = 2 ∣ a ∣ 2 + 2 ∣ b ∣ 2 + 2 ∣ c ∣ 2 − 2 a ⋅ b − 2 a ⋅ c − 2 b ⋅ c .
Also, ∣ a + b + c ∣ 2 ≥ 0 , which gives ∣ a ∣ 2 + ∣ b ∣ 2 + ∣ c ∣ 2 + 2 a ⋅ b + 2 a ⋅ c + 2 b ⋅ c ≥ 0 . Then A B 2 + A C 2 + B C 2 ≤ 3 ∣ a ∣ 2 + 3 ∣ b ∣ 2 + 3 ∣ c ∣ 2 = 2 4 9 . Thus, A B 2 + A C 2 + B C 2 is maximized when a + b + c = 0 .
Then a + b = − c , so ∣ a + b ∣ 2 = ∣ c ∣ 2 , and a ⋅ b = 2 4 9 − 9 − 2 5 = 2 1 5 . Then cos ∠ A O B = ∣ a ∣ ∣ b ∣ a ⋅ b = 3 ⋅ 5 1 5 / 2 = 2 1 . This means ∠ A O B = 6 0 ∘ , and sin ∠ A O B = 2 3 .
There is the question of whether such a triangle exists, i.e. if a + b + c = 0 can occur. This is left as an exercise for the reader. (Note that this condition implies the centroid of triangle A B C is O .)