This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Moderator note:
Indeed. We are unable to determine the value of f ( − 2 ) . In fact, we can only conclude that f ( x ) = x 4 for x ≥ 0 .
I just posted 16, knowing that there is a high chance of being wrong. But lately I'm kind of annoyed because many a problem here, only has to do with being careful with notation, or taking into consideration extreme or carefully chosen values. Kinda tired of this stuff, really... :-(
Log in to reply
I'm surprised that people actually agree to this. So you failed to solve the problems and then you blame them? Is that how you do things where you blame everything else except yourself? There's nothing wrong with the problems here in Brilliant. It's just that you either did careless mistakes or you lack the knowledge. I may sound a little rude here but I'm speaking the truth.
Go on, upvote his post and downvote all my posts. You're still not progressing if you don't accept your mistakes and learn from them. That's what I did all this time in Brilliant. You're merely agreeing blindly with whoever is opposing this problem while in reality your views may differ from theirs.
That's math. You have to know the rules because not everything can be applied with the same rule.
Here, in this case for x = − 2 , no solutions exist for x . It's pretty easy in a way but it's difficult for people inexperienced in math.
Log in to reply
Actually -2=sqrt(4) as (-2)^2=4.
Using REAL functional maths: f(y) = y^4 can be written as f(sqrt(x)) = sqrt(x) ^4 = x^2
This means that f(-2)=(-2)^4=16
Test on a calculator!
Edit: spelling error
Log in to reply
@Vincent Martin – Wrong. The sqrt function only returns the nonnegative result. If it returned two results, it wouldn't be a function.
@Vincent Martin – Plus 'Undefined' is not a REAL answer
sqrt(-2)=j*sqrt(2), therefore defined.
j (or i if you are a pure mathematician, I'm an engineer) is used in life for practical problems. Ie, in electronics j is used to denote lagging or leading of current against voltage.
Log in to reply
@Vincent Martin – Wrong. Division by zero is undefined. Taking the square root of a negative number is not the same as this.
Says the level one guy who cannot solve harder problems...
Log in to reply
what I'm supposed to answer to that? Your answer is childish. I tried to be constructive, and I express my annoyance about an issue happening lately in this page, about problems poorly stated, or for which their only point is being 100% carefully with notation, and no really-difficult-thing involved. I think this is not the way of having a problem published.
I don't care my "level one whatever"...
Log in to reply
@Jose Torres Zapata – Pardon me sir. I wasn't trying to hurt you. Please ignore my comment. Level doesn't matter. You are still a great guy anyways.
It would help the readers of you write that the question clearly shows x is the principal root
Now a days the problems are just playing around with the convention Has nothing to do with knowing math, but you need to know the convention ?
but answer makes sense as f is a function !!
Log in to reply
It's not the convention but contradiction of nature. It's really important to know this stuff while doing math to prevent unexpected errors.
If you browse through Brilliant, I'm sure you'll find many wonderful problems.
Without the proper understanding of math, will you be able to solve this problem correctly?
That's why most people overlooked the restriction of this function and answered wrongly. It's definitely legit and like what Arulx Z said, people tend to neglect some things and end up making mistakes and errors.
It's good that you didn't fall to the trap and answered correctly.
Log in to reply
I don't think that this is the point, the restriction is implicit anyway, if the argument cannot be defined, then obviously, the function is not defined there either.
It would help if the question explicitly stated that f was a real valued function and therefore couldn't take a value at x=-2
Log in to reply
It's not a matter of real or complex that x = − 2 doesn't exist here. It's because of the principal square root.
But it doesn't ask for x=-2, it asks sqrt(x)=-2 -> x=4... as (-2)^2=4.
This is how functions work you replace EVERYTHING in the brackets not just the x.
Then this gives f(-2) = ((-2)^2)^2 = 16! (obviously not (16)factorial)
f(sqrt(x)) = x^2 is THE SAME AS sqrt(y) = x^2 and solve for y... EVERYONE in GCSE and A Level would write that y = x^4 therefor if x = -2, y=(-2)^4 =16.
I don't understand why people are looking for PRINCIPAL roots as sqrt(4) has two roots 2 AND -2. The question make no mention of principal roots and no exam question would.
EVEN if it asked for sqrt(-2) this is defined as j*sqrt(2) then THIS squared would be equal to -2... so not undefined.
"Unable to determine" = "I don't know enough maths to write this question"!!!
I've seen this answer FAR too often on this site and it is usually used when the author thinks it sounds intelligent.
sqrt(-1) is used in lots of functions in engineering (real life situations), it is called j for engineers (or i for mathematicians). j is used in the definition of impedance for capacitors and inductors in electronics, it is used to signify oscillations in vibrational dynamics and SOO much more.
Log in to reply
logically there can never be a root whose value is negative(i think)
Log in to reply
@Vishal Vijaykumar – -2*-2 is not 4 is what you're trying to say? And then there is the concept of iota (i or j). He didn't state its a real valued function either although its irrelevant here.
we are not asked for solving and discussing principal values in reals but substituting a particular value of square root of x
Log in to reply
That's not true. The reason you're able to get an "answer" by substituting x = − 2 is because every real number has two square roots of the opposite signs.
The thing is, in functions we only have one output for each input, thus the principal square root which is a function. x = − 2 has no solutions. How can you have a number x whose principal square root is − 2 ?
Not convinced? √x=-2 - Wolfram|Alpha
Log in to reply
I only agree to the statement as the given question is a function. I don't agree with convention of principal root because if there was only principal roots for every equation then what's the significance of great euler's theorem , what is the significance of i !! nothing will exist !!
Nice argument finally. Can you elaborate and state where you find a contradiction if we allow non principal roots in the function. If you do that, this discussion would be settled.
I reasoned this way. If x is complex then the complex roots of x are always 2. For example 4 = ± 2 . So if we allow complex roots and x is a number whose root is -2 then x must be 4. So f(-2) = 4^2 = 16. Why this is wrong????
Log in to reply
This is the principal square root where x 2 = ∣ x ∣ . We take only the non-negative value.
For x = − 2 , no real number or even complex number satisfies this. Hence, no solutions of x exist.
Log in to reply
Thanks. I didn't know the "principal" square root.
Log in to reply
@Andrea Palma – No problem. We learn something every day, only if you're willing to learn. I've learned many things here in Brilliant too!
Exactly... Maybe these kids are unfamiliar with complex numbers...
Log in to reply
"These kids"? How rude. Perhaps you're the one who's unfamiliar with complex numbers.
Can you tell me a complex number x that satisfies x = − 2 ?
FYI, Calvin Lin represented his country two times in the IMO. He definitely knows what he's talking about.
Not only can √x not be -2 for any real x; for any non-real x, it can't even be real! So there is no complex x for which √x = -2.
Log in to reply
Why do people on this site not know sqrt(4))= +/-2?
What If x=2i^2
Log in to reply
x = 2 i 2 = 2 ( − 1 ) = − 2
But that's x , not x . No value of x can satisfy x = − 2 .
The point is, that for any complex x, -2 can never be the principal square root.
The problem is not that it's impossible for a solution to exist, it's that there are infinitely many solutions.
The function is well defined for all real numbers of the form x . But nothing is said about numbers not in that form, i.e. negative numbers.
So we may define the function in any way for negative numbers and f ( x ) = x 4 for nonnegative ones and the property will hold.
Note: If we add stronger restrictions, like being a polynomial function, we'll have unique solution.
Log in to reply
You cannot say f ( x ) = x 4 . Here's an example -
Consider the expression
x − 1 ( x − 1 ) ( x + 1 )
The expression is clearly undefined at x = 1 . But using your logic, one can simply argue that if you cancel out the x − 1 in numerator and denominator and then you are left with x + 1 . But this cannot be done because you can never divide by 0. Similarly, you can never get a negative value from x although you can manipulate it to do so. But the value received after manipulation will never satisfy the original expression.
Log in to reply
That is not correct. My logic doesn't imply that, and that kind of problem is not analogous to this. I'm not cancelling anything here, for example. And I'm not saying that your function equals x + 1 . I could say, on the other hand, that there are infinite (and uncountable) functions defined for all real numbers, which equal your function for all x = 1 . And that's a case similar to the problem.
As I answered Kennet Choo, you are assuming too much for the problem. You are assuming that the function is only defined for the real numbers of the form x . But that is never said. It's said the function must be defined for the real numbers of that form, but does not say what happens if not.
What it means from another point of view is that if f ( x ) = ? , g ( x ) = x 2 , h ( x ) = x , then f ∘ h = g , in all the domain of h . Taking f ( x ) = x 4 we get f ∘ h ( x ) = f ( x ) = x 4 = x 2 for any nonnegative number x , so the condition holds. Taking f ( x ) = x 4 for nonnegative real numbers and f ( x ) = sin x for negative real numbers also work. And that's the problem.
This kind of problem is very common in all mathematics. For example, the Riemann ζ function is a function such that ζ ( x + 1 ) = ∑ n = 1 ∞ n x + 1 1 , for all nonnegative real number x , and that is analytic in the complex plane.
And ζ ( − 2 ) = 0 .
http://www.wolframalpha.com/input/?i=Riemann+zeta(-2) https://en.wikipedia.org/wiki/Particular values of Riemann zeta_function
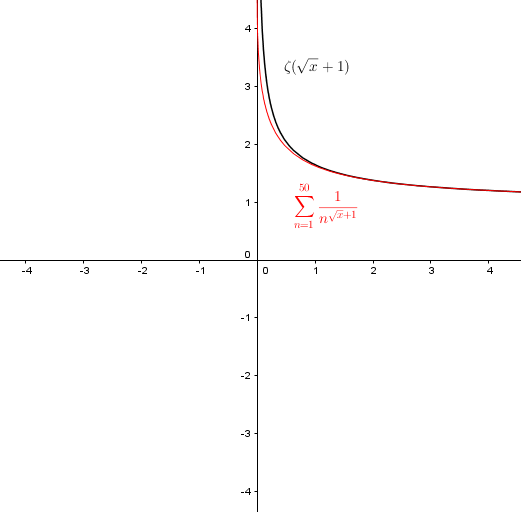
The picture shows a partial sum of the mentioned series, and the function ζ ( x + 1 ) . In the case of x = 0 the series becomes the Harmonic series, and so diverges. The function also goes to infinity there. It's grafically clear that the series and the Zeta function evaluated in x + 1 are the same for all nonnegative x .
In fact we do these kinds of continuations of functions more often. In linear algebra when we want a linear mapping we define it for the basis and "extend it by linearity". In group theory we define it for the generators of a group, and "extend by homomorphism property". The same we do with rings. In complex analysis we take a function defined in an open, connected set of the complex plane (In this case, the complex with real part greater than 1), which is infinitely differentiable there, and extend it to the whole complex plane. In Fourier Analysis we take a bounded (piecewise continuous) function defined on an interval ( 0 , π ] and extend it by parity to [-\pi,\pi] making it odd or even, depending of what we want, to make a Fourier sine or cosine expansion of the function.
Going back to this case, here we define a function for the nonnegative integers (i.e. The real numbers of the form x ) and see that is not enough to extend it to all real numbers. In particular, without any restriction f ( − 2 ) could be any real number.
You are asuming that if f ( z ) is ever defined, then z = x for some x , and that doesn't have to be true. If you want to use that, then you will have to prove it . You'll have to prove that thre isn't any function f defined for all real numbers, such that f ( x ) = x 2 for all nonnegative real numbers, using, of course, the definition of function and it's basic theorems .
Not really infinite solutions. By looking alone at the function f satisfying f ( x ) = x 2 , we know that the domain contains only non-negative real numbers.
In the case where x = − 2 , no value of x can satisfy that, not even complex numbers.
Log in to reply
No. We know the domain contains the nonnegative numbers. Nothing more. The fact that the function is defined for the nonnegative root of every nonnegative number does not force you to evaluate it always at numbers of that form.
The problem says to determine the value of f ( − 2 ) given that for all nonnegative numbers f ( x = x 2 . It doesn't really says what happens to the negative numbers (And that's the problem).
And in fact f ( x ) = x 4 satisfies the condition. f ( x ) = ( x ) 4 = x 2 .
Log in to reply
@David Molano – For f ( x ) = x 2 , x can be any number, including negative numbers (which will result in imaginary numbers).
However, x cannot be negative. While x can be any number, no number will have a negative number as the principal square root.
f ( x ) = x 4 satisfies the function f only if x ≥ 0 , which is x ≥ 0 (which is the domain of f ( x ) ).
Log in to reply
@Kenneth Choo – And what matters if x cannot be negative? f ( x ) = x 2 means " f evaluated in x is x 2 when the expressions are defined". It does not say anything else. It does not forbid anyone to take the value of f ( sin x ).
Taking f ( x ) = x 4 , g ( x ) = x , h ( x ) = x 2 , with domains R , R + ∪ 0 , R + ∪ 0 respectively satisfies the equation f ∘ g = h , because the value of f when x < 0 will never be used.
The problem is that you're thinking of f as " f restricted to the domain of g " , and that is not necessarily the case.
When you talk about how it satisfies the equation you're talking about the domain of the composite function f ∘ g , not the domain of f . I will mention something I mentioned above.
This kind of problem is very common in all mathematics. For example, the Riemann ζ function is a function such that ζ ( x + 1 ) = ∑ n = 1 ∞ n x + 1 1 , for all nonnegative real number x , and that is analytic in the complex plane.
And ζ ( − 2 ) = 0 .
http://www.wolframalpha.com/input/?i=Riemann+zeta(-2) https://en.wikipedia.org/wiki/Particular values of Riemann zeta_function

The picture shows a partial sum of the mentioned series, and the function ζ ( x + 1 ) . In the case of x = 0 the series becomes the Harmonic series, and so diverges. The function also goes to infinity there. It's grafically clear that the series and the Zeta function evaluated in x + 1 are the same for all nonnegative x .
In fact we do these kinds of continuations of functions more often. In linear algebra when we want a linear mapping we define it for the basis and "extend it by linearity". In group theory we define it for the generators of a group, and "extend by homomorphism property". The same we do with rings. In complex analysis we take a function defined in an open, connected set of the complex plane (In this case, the complex with real part greater than 1), which is infinitely differentiable there, and extend it to the whole complex plane. In Fourier Analysis we take a bounded (piecewise continuous) function defined on an interval ( 0 , π ] and extend it by parity to [-\pi,\pi] making it odd or even, depending of what we want, to make a Fourier sine or cosine expansion of the function.
Going back to this case, here we define a function for the nonnegative integers (i.e. The real numbers of the form x ) and see that is not enough to extend it to all real numbers. In particular, without any restriction f ( − 2 ) could be any real number.
You are asuming that if f ( z ) is ever defined, then z = x for some x , and that doesn't have to be true. If you want to use that, then you will have to prove it . You'll have to prove that thre isn't any function f defined for all real numbers, such that f ( x ) = x 2 for all nonnegative real numbers, using, of course, the definition of function and it's basic theorems .
Log in to reply
@David Molano – x cannot be negative. That's the thing that's very important here as no solution of x can satisfy x = a , where a < 0 .
As x ≥ 0 , x = sin x is true if and only if sin x ≥ 0 . You're bringing in unnecessary things here. We only have to know that x cannot be negative. That's all. Can you give me a value of x that satisfy x = a , where a < 0 ?
Log in to reply
@Kenneth Choo – I gave all kind of examples but you still don't understand what the problem is.
So in a change of strategy, I'll just ask two questions.
-
Why for f ( z ) to be defined, must z be a root of some number?
-
What are the restrictions in the domain of f to make sure f ∘ g is defined? Must d o m f = r a n g ?
Depending of your answer you should look again and study what's the composite function, and how is it defined.
Log in to reply
@David Molano – We're given the function f satisfying f ( x ) = x 2 .
Suppose g ( x ) = z = x , where z ≥ 0 , then
f g ( x ) = f ( z ) = z 4 , where z ≥ 0 .
g ( x ) = z = x = − 2
The domain of f is the same as the range of g .
Log in to reply
@Kenneth Choo – So, you say that for the composite function f ∘ g being defined, the domain of f mus be the same as the range of g . You're mistaken.
http://mathworld.wolfram.com/Composition.html
The only requirement to compose functions is that the domain of f contains the range of g .
Log in to reply
@David Molano – In a strict sense, the composition f ∘ g can be built only if g 's codomain (or range) equals f 's domain; in a wider sense it is sufficient that the former is a subset of the latter.
Log in to reply
@Kenneth Choo – That's wikipedia, isn't it? There codomain isn't the same as range. It's the same iff the function is surjective.
The strict sense is used in cathegories because the codomain isn't very important. We can require the codomain of g to be equal to the domain of f , but the range only if g is surjective. So. May the range of g be the same as the domain of f ? Yes, when g is surjective. Must they be? No. Not when it isn't surjective.
So Let's talk about range, instead of codomain. We only requiere the range of g to be a subset of the domain of f . May they be the same? Yes. Must they? No.
TL;DR? Wide or strict sense, the only requirement for the range of g (different in general from the codomain despite in high schools they are usually mentioned as equal) is that it's contained in the domain of f.
The fundamental problem is the f(sqrt(x)) notation. We don't care that sqrt(x) must be non-negative (which it must). We don't care what's inside the f( ) whether it's sqrt(x) or -2 or 😣 or (병신) or Trump's hair. The way it's written is that -2 has no relationship with sqrt(x) other than they are both inputs for the function f. If you wanted to define the domain of x, then a composite or a parametric is the way to express it. As it is written now, we cannot make any composite or parametric assumptions and must default to purely the relationship between sqrt(x) and x^2 which leads to: f(x) = x^4.
Trying to assume that this is a composite function is like trying to assume that a triangle is a right triangle "because it looks like one."
Log in to reply
@David Kim – How can you say that you "don't care" and that "-2 has no relationship with x " and yet solve the problem?
We take into account of everything and in the end we get that it's unable to determine for f ( − 2 ) . There're no assumptions here.
Log in to reply
@Kenneth Choo – The solution of the problem cannot be determined because there are infinite solutions. f may be defined as x 4 for nonnegative real numbers, and whatever for negative real numbers. And if g ( x ) = x , then the composite f ∘ g ( x ) will always equal x 2 , since the domain of f ∘ g is the same domain of g (Nonnegative real numbers), even if the domain of f is the quaternions (If we take f ( x ) = x 4 that could be the case). Let R o = R + ∪ { 0 } . We may have (taking f ( x ) = x 4 , g ( x ) = x , h ( x ) = x 2 ):
f : H → H
g : R o → R o ⊆ H
f ∘ g : R o → H
And f ∘ g = h .
All of this independently of the domain of f . And of the value of f in H − R o .
@Kenneth Choo – I can say -2 has no relation to sqrt(x) because of the lack of information telling me that I need to view that as a restriction on my domain. I see nothing telling me that it's a parametric or a composite. Therefore when I look at it, f(sqrt(x)) doesn't mean "the domain of x must be non-negative." Given the lack of extra information, the ONLY way I can view it is that the sqrt(x) and the x^2 is to ultimately establish that f(x) = x^4.
I will accept "undefined" only with more specific info. Otherwise the "undefined" answer is just trying to be too clever.
Log in to reply
@David Kim – When you look at x , you should know that x ≥ 0 where x can be any positive number to satisfy that inequality ( x can be a negative number to get an imaginary number). It's basic knowledge.
x can be 4 ( it can be a one to many function)
Log in to reply
A one-to-many relation is not the property of a function. A function can only be either one-to-one or many-to-one.
I disagree. If f( sqrt(x) ) = x^2 is saying "something needs to be done to root x to give me x^2." It is not saying "I first need to take the sqrt of the number, then put it to the 4th power."
If we say sqrt(x) = z and substitute, we see that f(z) = z^4. That means f(x) = x^4. The square root inside the left side f(x) is irrelevant.
Therefore f(-2) = 16.
Log in to reply
For x = z , z ≥ 0 .
The principal square root of x cannot yield a negative value of z .
Thus, f ( z ) = z 4 has the domain z ≥ 0 .
Log in to reply
And it's irrelevant that it cannot yield a negative value.
Log in to reply
@David Molano – It's definitely relevant. You're trying to break the rule of the principle square root here.
Log in to reply
@Kenneth Choo – Nope. You are Trying to break the definition of function.
Log in to reply
@David Molano – The definition of function is that each input is related to exactly one output. How am I breaking that definition? You were saying that there're infinitely many solutions. How is that respecting the definition of function? The principle square root here respects that definition. If it's not the principle square root, how can f ( x ) = x 2 be a function here?
Log in to reply
More exactly, the concept of composite function (Look at my other comment for more details). And the concept of the principal root does not have anything to do with the essence of the problem.
My other comment: I gave all kind of examples but you still don't understand what the problem is.So in a change of strategy, I'll just ask two questions.
-
Why for f ( z ) to be defined, must z be a root of some number?
-
What are the restrictions in the domain of f to make sure f ∘ g is defined? Must d o m f = r a n g ?
Depending of your answer you should look again and study what's the composite function, and how is it defined.
More exactly, the concept of composite function (Look at my other comment for more details). And the concept of the principal root does not have anything to do with the essence of the problem.
It might be a solution. But it's not unique in any way.
I am a mathematician, and I completely disagree with this explanation. The question in no way "clearly asks for the principal root". If there's any ambiguity, it's in the definition of x, but I'm going to assume the question meant to imply "... for any and all x". Otherwise, it only has to hold true for an arbitrary value of x.
Before I go on, I want to propose that this is a regional notation difference. x does not mean "positive root of x", at least here in the United States. It may do so elsewhere. The notation ± x is generally redundant, but used as a reminder.
That said, taken as written, the satisfied equation actually implies that the function's domain extends into the positive and negative reals, since it must be satisfied for all roots. As such, it must be that f ( x ) = f ( − x ) , f ( − 2 ) = f ( 2 ) , and so f ( − 2 ) = 1 6 .
Some people seem to be getting confused by the function g ( x ) = f ( x ) . If this function was required to exist, it would cause problems, because it drives us into imaginary numbers and restricted domains. However, we can't use g ( x ) in our reasoning, because it can't be a proper function due to producing 2 results, however temporarily.
Is it not that the square root of 4 is +/-2 as both 2 and -2 sqaured are both 4
Log in to reply
It is. But that's the case when we have the equation x 2 = 4 . Then x = ± 2 . But you *cannot say that 4 = ± 2 because x only returns the positive value.
It has been said many times here but I'll say it again.
It's the principle square root where we only take the non-negative number.
4 = 2
For x = − 2 , no solutions exist for x .
To get an undefined answer, the function should read f(x) = (sqrt(x))^4 which equals x^2. Then the answer to the question would be correct. Or he could have written "g(x) = x^4 and f(x) = sqrt(x). What is g(f(x)).?"
However as it is written, it is saying that f(?) = (?)^4 and the correct answer is 16. This is how function notation works.
Isn't the answer -16? x=4i because there is no restriction on x.
Log in to reply
For x = − 2 , no solutions exist.
The restriction would be x ≥ 0 . We then can conclude that f ( x ) = x 4 , x ≥ 0 .
If x = 4 i , then
x = 2 i = 2 4 ( − 1 ) .
Question is incomplete, without specification of domain of x ,this que will have 2 answers. With domain (x is real) there will be 1 answer
Why cant you just plug in -2 to f(x)=x^4 to get 16? 🤔
Log in to reply
Took me a while, to figure out, because I though the same by thinking that the complex buddy will deal with this problem. But the real problem is that there is no such number x, that Sqrt[x]= -2. It would work in the other way round: Sqrt[-2]=x (x=i*Sqrt[2]), but it does not work this way. A pretty tricky problem.
Because f ( x ) = x 4 is only defined for x ≥ 0
Log in to reply
Why can't x = i^4 * 4 which will give you x= i^2 * 2=-2
Log in to reply
@Mohamed Wafik – If x = 4 i 4 , then x = 4 as i 4 = 1 .
Thus, x = 2 = − 2 .
Actually, i 4 = i 2 . In fact, i 4 = 1 because i 4 = 1 and 1 = 1 .
Thus, i 4 = 1 .
Just for extra information, ( ± i 4 = ± 1 ) which are the 2nd roots of unity.
@Mohamed Wafik – I didn't understand your point but you can try substituting x into x . If you take the positive root, you will never get the answer as − 2 .
1) So does that mean f(x) = x 2 is true only for x>=0 ? 2) And x we assume as positive root of x. But that doesn't stop (- x ) being a root of x.
Log in to reply
1) No, in this case from the given function f ( x ) = x 2 , we can conclude that
f ( x ) = x 4 for x ≥ 0 .
For a function of g ( x ) = x 2 , it is true for all real numbers of x .
2) This is the principal square root, defined as x 2 = ∣ x ∣ where
∣ x ∣ = x , if x ≥ 0
∣ x ∣ = − x , if x < 0 .
Your input x cannot have two output ± x , thus x is the principal root which is the non-negative value. Do remember that a function has the property that each input is related to exactly one output.
*principal root
To explain it a little more rigorously than what people have already said:
For any number y satisfying y = x for some x , we know that f ( y ) = x 2 .
Since x means the principal square root of x , and there is no number whose principal square root is a negative real number, we cannot deduce anything about the value of f ( y ) if y < 0 . Hence 'Unable to determine'.
You're taking for granted that x is a real number, to talk about the principal determination of the square root. My point is, you have to assume that \sqrt{x} means the positive or principal determination. But, why do we have to assume that x is a real number? Trying to cheat your audience, by lack of information, gets people annoyed. It gets me annoyed, at least.
Yes, surely you can argue that 99% of times, or if nothing else stated, x is a real number. But I can show you examples in brilliant, in the other sense, ie equations using x, but with solution in the complex field, and the cheater-author arguing that, if no other thing stated, you cannot suppose x to be real.
This kind of problems, tricky only by little details, are getting me bored.
It would be nice if we have a chatterbox, or text field, or whatever, to allow us users say this things, like "you have to be more specific for x, if you don't want to trick me". Or make a little spoiler, and mark the question like, "fine point cheat wannabe" For the question to be answerable without any doubt, you have to state that x is real, AND that \sqrt{x} means whatever...
Log in to reply
Eh, how do you work that out? Please give me an example of a complex number whose principal square root is a negative real number.
Log in to reply
my point is that when you see x you think of x being a real number, when you see . you think about principal determination on square root, and so on. You should be warned that everything is as usual. Or we should have a textbox where you can express your concerns about the lack of info for the problem. For me, the posing of the problem was uncomplete. My line of thoughts was like this: I received the email from brilliant, saying "many people are getting this wrong". I looked at the problem, and I consider "should be Unable to determine", but if people are getting wrong might be 'cause x is not a real number, so x perphaps doesn't mean square root in the usual sense, principal determination, but only "inverse of square", so both cases are to be considered. (as I see things, a lack of information). In that case x could be interpreted like ± x , so x = 4 , x = 2 but ALSO x = − 2 , then x 2 = 1 6
If you consider x ∈ Z 2 0 , the problem has no solution, and hey! nothing is said about x . Or, for that matter, you can define x to be another thing different from square root.... So, lack of information in the stament of the problem
Log in to reply
@Jose Torres Zapata – You accused me of neglecting to consider the possibility that x is an arbitrary complex number as opposed to a real number. So I asked you how you reached this conclusion.
Logic tells me that the only way you can prove that I neglected to consider complex numbers is by showing the existence of a complex number x such that x is a negative real number, whether by giving an explicit example of such an x or by otherwise giving a sound proof that such an x exists.
Or are you saying that the concept of a principal square root exists only in the context of the real number domain? This isn't true - principal square roots are defined for complex numbers as well. The definition is the one whose argument is in the interval ( − 2 π , 2 π ] .
@Jose Torres Zapata – You should know that functions have the property that each input is related to exactly one output. That is why this is the principal square root where we take the non-negative root. If each input can have two output values then it's not a function. The principal square root is a function.
There's no concern of real numbers or complex numbers here as no numbers, not even complex numbers, can satisfy x = − 2 . Can you think of a number?
There's no lack of information or whatsoever. This problem is not trying to cheat anyone, but testing your knowledge. You get tricked because you lack the knowledge, and you get annoyed over it and blame the problem itself? Why don't you learn from your mistakes so you don't repeat them again instead of being angry over it?
I'm going to post something that comes from Complex Analysis, and say that the answer could be 16.
Any number z in the complex plane can be written in countably many different ways, because of the equivalence between e 2 n i π , n ∈ Z , and 1 . This leads to choosing a so-called "principal branch", which defines the your principal range of θ when you write z = ∣ z ∣ e i θ , where θ = ar g ( z ) . Whatever branch you work in, the "principal square root", ⋅ , is defined to be
z ≡ ∣ z ∣ e i θ = ∣ z ∣ e i θ / 2
Supposing that we choose the branch to be θ ∈ [ 0 , 2 π ) (as others appear to have done), we see that − 2 cannot be written in the form ∣ z ∣ e i θ / 2 , and thus we are unable to determine the answer.
Now suppose we choose our principal branch to be θ ∈ [ π , 3 π / 2 ) instead. We can write 4 = 4 e i ( 2 π ) , and hence the principal square root of 4 in this branch is 2 e i π = − 2 . Thus we get that f ( − 2 ) = 1 6 e 4 i π = 1 6 .
Of course, since the question doesn't specify a principal branch (or corresponding branch cut in the complex plane), you could argue that that we really are "Unable to determine" the answer, because it depends on the principal branch you choose. (But this would mean that questions like "Is 4 = 2 or − 2 ?" are also ambiguous because it could be either, depending on the branch of the complex plane that you choose.)
And of course this is all being overly pedantic, but I never get the chance to chat about complex analysis!
As an extra point, choosing branch cuts and principal branches leads to interesting conclusions, such as:
Is g ( z ) = z 2 − 1 an even or odd function?
Of course, because it has z 2 , it seems that it is clearly an even function. However, two scenarios arise:
1) branch cut ( − ∞ , − 1 ] ∪ [ 1 , ∞ ) gives you that it is an even function;
2) branch cut [ − 1 , 1 ] gives you that it is an odd function
P.S. I've nicked this example from the Cambridge University Mathematics Tripos: Further Complex Methods first problem sheet .
Ultimately the point I'm trying to make is that the principal square root does not have to output a non-negative number--it depends entirely on the branch/branch cut you take in the complex plane.
We want to find a x such that x = − 2 .
But for any positive, real numbers x , we have x ≥ 0 .
And for any negative, real numbers y , the square root y will always have at least an imaginary part i .
Even if we try to plug in a complex number for x , we get by De Moivre that the imaginary part of the square root of a complex number (in polar coordinates) is only 0 if and only if θ = 0 . But if θ has this value, the we have positive, real numbers again.
I agree with Arulx on the solution but not the reason. We know that f ( x ) = x 2 , but not that that is the only rule. Based on that rule, we have no knowledge of f ( − 2 ) . If that were the only rule defining the function, f ( − 2 ) would not exist, which is different than saying we are unable to determine. If there were another rule defining the function f ( x ) on negative numbers, perhaps f ( − 2 ) would be meaningful. It is that ambiguity which, in my opinion, is most relevant to the answer.
A layman way of viewing it is that
f ( ( x ) ) => f ( − 2 ) , then there must be some value that x = − 2
We don't even know the domain of f. We can't assure that -2 belongs to said domain.
If any solution exists, − 2 = x , which is impossible because the question clearly asks for the principal root. Principal root can only output non-negative values for any real value of x .