Inverse Trig Puzzle

Geometry Level 2

True or False?

$\sin ^{-1} \left( \sin \theta \right) = \theta.$

The domain of $\sin \theta$ is all real numbers.

True False

5 solutions

Daniel Liu
Sep 1, 2015

Note that the range of $f(x)=\sin^{-1} x$ is $\left[-\dfrac{\pi}{2},\dfrac{\pi}{2}\right]$ and the range of $f(x)=x$ is $\mathbb{R}$ .

With this in mind, if we pick a $|\theta| > \dfrac{\pi}{2}$ it is easy to see the equation is false.

Both True and False are wrong. It's true for some x and false for other x. Just because there exists an x for which the equation is false, does not mean that the equation is false.

David Hammer - 5 years, 9 months ago

Just because a broken clock tells the correct time twice a day, does not mean it's usually broken but working occasionally. If ever a mathematical premise is false, then it it is always considered false. Otherwise we'd say that 2x = x^2 is 'both true and false' because it's true when x=2, false otherwise.

Nigel Denning - 5 years, 9 months ago

+1 for this

Melvin Loquero - 5 years, 9 months ago

Can we also say that x/x is NOT (always) equal to 1? I thought about substituting x = i, so can we say that x/x = i/i but ≠ 1? Or can we even possibly do this?

Hustino Laserna - 5 years, 9 months ago

@Hustino Laserna – Or how about substituting x with 0 ? It too is not possible !

Aritra Roy - 5 years, 9 months ago

@Aritra Roy – There is a name for that case "undefined quantity"

Ahmed Obaiedallah - 5 years, 8 months ago

The question should have stated it as an identity to be disproved, as opposed to an equation which you quite correctly flag up

David Orrell - 5 years, 8 months ago

In Mathematics, if there is one case where the statement is false, then the entire statement is false.

Joseph Rangitsch - 5 years, 9 months ago

Then the question must be incomplete. One should mention clearly about the range in question itself.

Kumar Patchakanthala - 5 years, 8 months ago

That x may be + or - x., which matters the most. As it is not specified it is false

Abinaya Muthiyalram - 5 years, 8 months ago

Agree with David Hammer.

Lahiru Ranasinghe - 5 years, 5 months ago

I think it sort of does. An equation pretty much has to be true for the range.

William Cummings - 5 years, 9 months ago

Yes, the question itself was wrong.

Khai Seox - 5 years, 9 months ago

Questions are never wrong its your perception thats wrong

bhargav pavuluri - 5 years, 9 months ago

@Bhargav Pavuluri – Then you feel free to ask any ambiguous question without any possible answer? Your statement is right in some ways, questions are never wrong but the askers were wrong.

Khai Seox - 5 years, 9 months ago

Is it true that $\sin \left( \sin^{-1} x \right) = x$ ?

Calvin Lin Staff - 5 years, 9 months ago

what if x is larger than 1 or less than -1?!

Khai Seox - 5 years, 9 months ago

its always true

bhargav pavuluri - 5 years, 9 months ago

Yes because the graph of this equation will just be a straight line $y=x$ for $x$ lying between $1$ and $-1$

Saarthak Marathe - 5 years, 9 months ago

This is also false, because the domain of $\sin^{-1}x$ is $[-1,1]$ so plugging in any $|x| > 1$ will give an undefined equal to a number value.

However, it is true for all $x$ such that both sides are defined.

Daniel Liu - 5 years, 9 months ago

Taking the extension to complex numbers does make it true for all complex $x$ .

Ivan Koswara - 5 years, 9 months ago

u should put a value in the domain.

bhargav pavuluri - 5 years, 9 months ago

Because cyclic nature of sin arcsin( sin x ) = x+2kπ, when k is integer. BUT here we have angle theta in planar geometry context, I suppose, and that meant theta is between 0 and 2π. So, if you talk about function use appropriate letters for arguments

Mari Za - 5 years, 9 months ago

What is the difference between the variable $x$ and the variable $\theta$ , without stating any other restrictions on them?

Calvin Lin Staff - 5 years, 9 months ago

The difference is that we assume the variables to represent different things: this may not seem very mathematical because it is implicit, but it is necessary when there is not enough information to go off. Was $\theta$ supposed to be a natural number, a complex number, a hyperreal number, or the number 5208? Also, you should specify that you mean $\arcsin (\sin \theta)$ rather than the reciprocal of $\sin (\sin \theta)$ if that is what you intended to mean.

Will Cxp - 5 years, 9 months ago

In Euclidean geometry Theta+2Pi=Theta :) that is not true if you have an argument x. Trigonometric Identitie sin(theta) = a/c is not same as trigonometric function sin(x). Funny? Cyrcle or periodic, or both...

Mari Za - 5 years, 9 months ago

But is it not implied that you are working within the domain of the function? In general (by def) f^-1(f(x)) = x, but it's understood that you working within the appropriate domain. So, for example, if g(x) = 1/x, you can say that g^-1(g(x)) = x even though f(x)=x can be zero and g(x) can't be, because 0 is not within the domain (or range) of g(x).

David Ortiz - 5 years, 9 months ago

I agree with David. I get the point of these sorry of questions, but in practice most people take those things for granted and troubleshoot if a conflict comes up.

Herman Pittman - 5 years, 9 months ago

I was actually under the impression that any $f(x)$ (and $f^{-1}(x)$ also) could be interpreted as either a mapping or a function depending on context (or whichever is specified), as one often wants to find all or multiple solutions to an equation, in which case restricting a map to a function will not do. Perhaps someone could verify that this is the case or correct me if not. Either way, I honestly don't see the point in restricting a map to a function in the context of pure Mathematics, as it only leads to mistakes and confusion such as this problem indicates.

Will Cxp - 5 years, 9 months ago

It makes no sense to ask if an equation is true or false - it either has solutions or it doesn't. An identity can be true or false but this question uses an equals sign not an equivalence sign. It's a flawed question.

Dug Duggan - 4 years, 8 months ago

I thought it was true..as a layman my reasoning was sin Θ = sin Θ, so by inverse function i can write sin ^-1 (sin Θ) = Θ...What i'm missing here..m confused...plz help...

Anindya Mukherjee - 5 years, 9 months ago

u cant apply inverse on both sides. just like squre root. (1 * 1 ) = (-1 * -1) but $1 \neq -1$ . ArcSine is of same type

bhargav pavuluri - 5 years, 9 months ago

It is false because sine^-1 is not equal to 1/sine. 1/sine is equal to cosecant. sine^-1 can be written as arcsine to avoid confusion.

Shayn Amores - 5 years, 9 months ago

so i get that they said its false but i really dont see how it is false. ive done it out and it should definatly be true. can anyone give and example where it isnt

walker champeaux - 5 years, 9 months ago

Remember the basic Trigonometric functions sine, cosine, tangent, cosecant, secant and cotangent. If you remember the very basic definitions of those Trigonometric functions, then you will know that 1/sine is equal to cosecant rather than sine^-1. Sine ^ -1 is different from cosecant. Do not be fooled by how it is being written. If you graph Trigonometric Functions and Inverse Trigonometric functions, you will see the big difference. To avoid confusion, sine^-1 or inverse of sine can be written as arcsine

Shayn Amores - 5 years, 9 months ago

But isn't 1/sin= sin^-1

Roshan Rai - 5 years, 9 months ago

No. 1/sine is equal to cosecant. sine^-1 can be written as arcsine to avoid confusion.

Shayn Amores - 5 years, 9 months ago

Why so? Also, what about when I use degree instead of radian? in that case, 560 degrees, say, is just (560-360) degrees, which is valid!

Vinay Seth - 5 years, 9 months ago

I've just typed sin^-1(sin(pi/2) into a calculator and it equalled pi/2...?

Dominic Parnell - 5 years, 7 months ago

But it's not false it's just not true in all cases. The question was flawed

Miles Johnson - 4 years, 10 months ago

The inverse sine function does not exist unless you restrict the domain of the sine function to between -pi/2 and pi/2 (making it a one to one function) so you can't select theta>pi/2

Dug Duggan - 4 years, 8 months ago

Note that since $-1 \leq \sin \theta \leq 1$ for all values of $\theta$ , we can apply the inverse sine function to this value.

In particular, if $\theta = 4$ , then $sin^{-1} (\sin 4) = \( \pi - 4$ .

Calvin Lin Staff - 4 years, 8 months ago

Khai Seox
Sep 12, 2015

I think the question itself was wrong, it didn't gave a range of the angle.

Technically, the question isn't wrong, but is written ambiguously and in a deliberately misleading manner. Before even beginning to solve this problem it is clear to see that it is a trick question, and giving a range for $\theta$ would draw attention to the domains and ranges of $\sin$ and $\sin^{-1}$ , and imply the trick being used. This is how the problem is misleading—by trying to manipulate the way one thinks—and it is generally acceptable for a trick question to be misleading.

However, the question doesn't indicate the meaning of $\sin^{-1}$ (which could be interpreted as the inverse mapping of the $\sin$ function, the inverse function of the $\sin$ function, or the reciprocal of the $\sin$ function). As such, the question is ambiguous; it is impossible for anyone to be certain that their answer will be accepted (without additional information). This makes the question unfair.

Will Cxp - 5 years, 9 months ago

I said the question was wrong because its "proposition" is not a really proposition: A proposition must either true or false in all cases (by any value of $\theta$ . I don't call this proposition , this is a proposition-function which depends on the angle $\theta$ . This question is right if and only if they provide a range of $\theta$ (e.g. $\forall \theta \in \mathbb{R} : sin ^{-1} (sin \theta ) = \theta$ )

Khai Seox - 5 years, 9 months ago

By 'proposition' do you mean conjecture? It is definitely not true that a conjecture has to be true in all cases or false in all cases (as Nigel Denning already told David Hammer in the replies to Daniel Liu's solution). Even with the example range you've given the conjecture is still sometimes true and sometimes false (by Daniel Liu's explanation) if we take $\sin^{-1}$ to be the inverse $\sin$ function.

Will Cxp - 5 years, 9 months ago

@Will Cxp –

Sometimes true and sometimes false

So, both 'true' and 'false' answers are sometimes correct and sometimes incorrect?! If the question was $\forall \theta \in \mathbb{R} : sin ^{-1} (sin \theta ) = \theta$ or $\exists \theta \in \mathbb{R} : sin ^{-1} (sin \theta ) = \theta$ , there's no "sometimes" anymore.

Khai Seox - 5 years, 9 months ago

@Khai Seox – I'm not entirely sure what you're asking. Whether the conjecture is true or false depends on whether or not the equation is true in all cases.

Let's stick with $\sin^{-1}$ representing the inverse $\sin$ function. For $\theta \in \mathbb{R}$ there are some values of $\theta$ (namely those greater than $\pi / 2$ or less than $-\pi / 2$ ) for which the equation is false and the equation is true for the remaining values. Therefore, if we are taking $\theta$ to be any real number, the conjecture is false because the equation is not satisfied in all cases.

Before, when I said the conjecture would sometimes be true and sometimes be false, I was meaning for a single value of $\theta$ , although the conjecture actually implies that the equation must be satisfied for all values of $\theta$ in order to be true.

Will Cxp - 5 years, 9 months ago

@Will Cxp – I think you don't understand me, I haven't asked you anything, I just explained.

What I told is not the answer of the question, I said the question itself was wrong don't mean the answer is 'false'. I mean the question is ambiguous, but math must not ambiguous, math is the logic of the certainly/definitely and clearly things. So, the question may not considered as a good mathematical question.
If I answer this question, I will tell that $sin ^{-1} (sin \theta ) = \theta \Rightarrow \theta \in [-\frac \pi 2; \frac \pi 2]$ (just like "find x" with x is $\theta$ ). But the question provided only 'true' and 'false' as the possible answers. then my "correct/incorrect" is "sometimes" anyway. So, the question itself is invalid .
If the asker only wants either 'true' or 'false', then the question should be changed become either $\forall \theta \in SetOfTheta : \ldots$ or $\exists \theta \in SetOfTheta : \ldots$ or $sin ^{-1} (sin \theta ) = \theta \Rightarrow \ldots$ .... Anyway, the question must be certainly.

Khai Seox - 5 years, 9 months ago

Why are people making an obvious question way harder than it is. This is a trick question, if you got it right good for you. If you didn't nobody cares.

Stephen Hawkings - 4 years, 11 months ago

Kishore S. Shenoy
Oct 15, 2015

Let $\sin x = \sin y,~\Rightarrow y = \sin^{-1}\left(\sin x\right)$ , where $x$ is a general angle. So, $y = n\pi + (-1)^nx$ so that $y$ is a principle angle of $\sin$ function, $y\in\left[-\dfrac{\pi}2,\dfrac{\pi}2\right]$

In the above equations, we should take appropriate value of $n$ to get value of $y$ in the principle domain.

So, for instance, when $x \in \left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right]$ , $n = 0,~y = x$

And when $x\in\left[\dfrac{\pi}{2}, \dfrac{3\pi}{2}\right]$ , $n = 1,~y = -x+\pi$

Et Cetera...

This $y$ and $x$ relation for each case can be easily obtained from the graph of $\sin^{-1}(\sin x)$

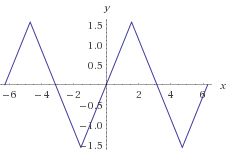
Think about it...!

Moderator note:

It's not clear to me what you are doing here. You should explicitly state what it is you want to show.

@Calvin Lin , sir: I think I'm clear now. (Done some edits)

Kishore S. Shenoy - 5 years, 8 months ago

Nope, it is still not clear to me what you are trying to say. You may think that you know what you want to say, but that is not expressed in what you have written. The various issues are

$\sin^{-1}$ is only valid on a limited domain. Why must the equation be valid?
As an explicit example, take $x = 0$ . What are the values of $y$ ? As we substitute values for $n$ , we get $y = 0, \pi, 2 \pi 3 \pi , \ldots$ . But if we look at your graph, we only get $y = 0$ .
So you are saying that we cannot have $\sin 5 \pi = \sin (- 5 \pi )$ since it doesn't fit into $y \in [ - \frac{\pi}{2} , \frac{ \pi}{2}$ ?

Calvin Lin Staff - 5 years, 8 months ago

No, I'm saying that y is a principle angle and thus will only be 0.

Kishore S. Shenoy - 5 years, 8 months ago

domain of sinx is all real number.so what, for any value of x, sinx ranges from -1 to 1.hence the left side return to x.I think the ans is wrong.

Enamul Hoque Sumon - 4 years, 1 month ago

I'm not sure what you mean by "hence the left side return to x.".

Are you saying that $\sin^{-1} (\sin 2 \pi ) = 2 \pi$ ? If so, what is $\sin^{-1} 0$ ?

Note that the inverse is a (single-valued) function.

Calvin Lin Staff - 4 years, 1 month ago

Suraj Gaddam
Sep 24, 2015

Let's take the angle as -90,then the statement is false,the correct answer should satisfy all conditions.So,its false

Some angle should have been provided... The answer is partially wrong and partially correct

Tanmoy Sarkar - 4 years, 6 months ago

Faisal Ahmed
Sep 17, 2015

Both True and False are wrong. It's true for some x and false for other x. Just because there exists an x for which the equation is false, does not mean that the equation is false.

Inverse Trig Puzzle

5 solutions

Moderator note:

0 pending reports