Inspired by "Squeeze it in"
I want to squeeze in the largest possible equilateral triangle into a square with side length 30. If the side length of such a triangle can be represented in the form 3 0 x − 3 0 y , find x + y .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
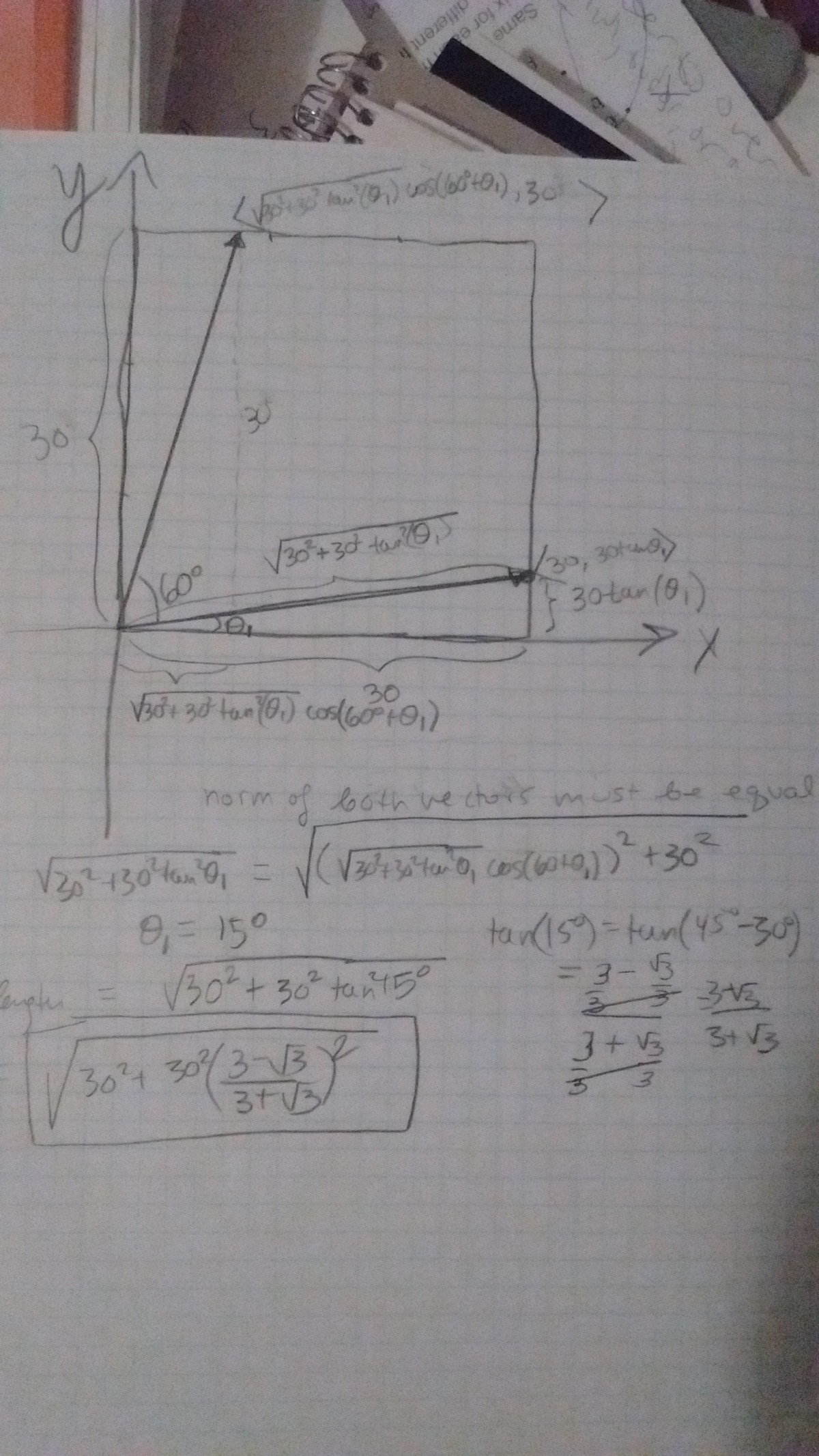
What I boxed in the picture can be rewritten as 3 0 6 − 3 0 2 , and 6 + 2 = 8 .
How do you know this configuration produces the largest equilateral triangle?
Log in to reply
Using the 2 points I got, I did test the length for the third side and it is confirmed that all three sides have the same length. I suppose I could have written a vector for the third side. In this problem, the length of the two legs we are dealing with depends on theta, and I solved for the theta that makes the lengths the same. One leg is completely extended from one side to another such that both sides can be the same length with 60 degrees between them so I believe this is a correct approach, unless of course, you found a way to get a larger triangle
Log in to reply
Max length but wouldn't fit is hypotenuse Min length but still wouldn't fit is 30
Log in to reply
@Hobart Pao – The triangle you've found is indeed the largest, but proving it requires more work.
The vertex angles of an equilateral triangles are 60 degrees, so at B 30 degrees are left to be shared by the pair of a triangle sides and a square sides. However sides of an equilateral triangle are equal this is only possible if 30 degrees are shared equally.
S o ∠ A B F = ∠ E B C = 1 5 . Δ s A B F ≡ E B C , ⟹ Δ B E F i s i s o s c e l e s w i t h ∠ E B F = 6 0 . S o i t i s e q u i l a t e r a l w i t h s i d e B E = C o s 1 5 B C = 4 6 + 2 3 0 = 3 0 ( 6 − 2 ) . ∴ x + y = 6 + 2 = 8