$\int _{ 0 }^{ \pi }{ { \arcsin { (\cos { (x) } ) } }^{ 2 }dx }$

As we know that $\arcsin x+\arccos x=\frac{\pi}{2}$ for all $x$ so, we can simplify the expression to be integrated :-

$\displaystyle \int_0^{\pi}\left(\arcsin\left(\cos x\right)\right)^2dx$

$\displaystyle =\int_0^{\pi}\left(\frac{\pi}{2}-\arccos\left(\cos x\right)\right)^2dx$

$\displaystyle =\int_0^{\pi}\left(\frac{\pi}{2}-x\right)^2dx$

$\displaystyle =\frac{\left(\frac{\pi}{2}\right)^3}{3}-\frac{\left(\frac{\pi}{2}-\pi\right)^3}{3}$

$\displaystyle =\frac{\pi^3}{12}$

I think you meant $I=\int_0^{\pi} \left(\arcsin (\cos x)\right)^2dx$

Using symmetry we get $\displaystyle \int_0^{\pi}\left(\arcsin (\cos x)\right)^2dx=2\int_0^{\frac {\pi}{2}} \left(\arcsin (\cos x)\right)^2dx$

Now using that $\displaystyle \int_0^a f(x) dx=\int_0^a f(a-x)dx$ with $a=\pi /2$ and $f(x)=(\arcsin (\cos x))^2$ we get $\displaystyle 2\int_0^{\frac {\pi}{2}} \left(\arcsin (\cos x)\right)^2dx=2\int_0^{\frac {\pi}{2}} \left(\arcsin (\sin x)\right)^2dx$

Now using $\arcsin (\sin x) =x$ we get $\displaystyle 2\int_0^{\frac {\pi}{2}} \left(\arcsin (\sin x)\right)^2dx=2\int_0^{\frac {\pi}{2}}x^2 dx= \frac {\pi^3}{12}$

$\begin{aligned} I & = \int_0^\pi \sin^{-1}(\cos x)^2 dx \\ & = \int_0^\frac \pi 2 \sin^{-1}(\cos x)^2 dx + \color{#3D99F6} \int_\frac \pi 2^\pi \sin^{-1}(\cos x)^2 dx & \small \color{#3D99F6} \text{For }x \in \left[\frac \pi 2, \pi\right], \cos x \in [-1,0] \implies \sin^{-1}(\cos x) \in [-1,0] \\ & = \int_0^\frac \pi 2 \sin^{-1}(\cos x)^2 dx + \color{#3D99F6} \int_0^{-\frac \pi 2} \sin^{-1}(\cos x)^2 dx & \small \color{#3D99F6} \text{Since } \sin^{-1} (\cos x)^2 \text{ is even} \\ & = {\color{#3D99F6}2} \int_0^\frac \pi 2 \sin^{-1}({\color{#D61F06}\cos x})^2 dx & \small \color{#D61F06} \text{and } \cos \theta = \sin \left(\frac \pi 2 - \theta\right) \\ & = 2 \int_0^\frac \pi 2 \sin^{-1}\left({\color{#D61F06}\sin \left(\frac \pi 2 - x\right)}\right)^2 dx \\ & = 2 \int_0^\frac \pi 2 \left(\frac \pi 2 - x \right)^2 dx \\ & = - \frac {2\left(\frac \pi 2 - x\right)^3}3 \bigg|_0^\frac \pi 2 \\ & = \frac {\pi^3}{12} \approx \boxed{2.584} \end{aligned}$

Once you realize that the definition of arcsin and arcos add up to $\pi/2$ , we quickly see that the integrand is just a parabola and touches the x-axis at $\pi/2$ .

There's a little trick to integrating powers of $x$ . If you integrate $x^2$ from 0 to 1, it gives you 1/3. For larger regions for 0 to $a$ , you scale up the answer by $a^3$ .

If you graphed the integrand, you'd notice that there are two equal areas that fit the description.

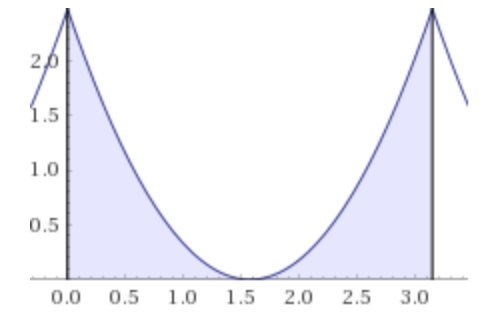
thus, the integral is just $\displaystyle 1/3\times 2\times \left(\frac{\pi}{2}\right)^3=\frac{\pi^3}{12}$ .

$\arcsin(\cos{x})=\dfrac{\pi}{2}-x$ .

\text{Thus, the eq is equal to } \quad \displaystyle \int_{0}^{{\pi}{2}} {(\dfrac{\pi}{2}-x)^2}}=\dfrac{2}{3} \cdot (\dfrac{\pi}{2})^3=2.58\uparrow{3}86 \cdots =\boxed{3.584}.)

$\begin{aligned} \int_0^{\pi}(\arcsin(\cos(x)))^2~dx&=\int_0^{\pi}\left(\arcsin\left(\sin\left(\frac{\pi}2-x\right)\right)\right)^2~dx\\ &=\int_0^\pi\left(\frac{\pi}2-x\right)^2~dx\hspace{50pt}\text{Since }\arcsin(\sin(y))=y\text{ for }y\in\left[-\frac{\pi}2,\frac{\pi}2\right]\\ &=\frac{\pi^3}{12}\\ &\approx2.58385639 \end{aligned}$

I don't think this question deserves Level4 in calculus.

$\int \sin ^{-1}(\cos (x))^2 \, dx \Rightarrow -\frac{1}{3} \sqrt{\sin ^2(x)} \csc (x) \sin ^{-1}(\cos (x))^3$ which gives $\frac{\pi ^3}{12}$ as a result.

Because ${ \arcsin { \left( \cos { \left( x \right) } \right) } }^{ 2 }$ is symmetrical about ${\pi }/{ 2 }$ , the integral expression can be rewritten as

$2\int _{ 0 }^{ \frac { \pi }{ 2 } }{ { \arcsin { \left( \cos { \left( x \right) } \right) } }^{ 2 } } dx$

Using the property that $\int _{ a }^{ b }{ f\left( x \right) } dx=\int _{ a }^{ b }{ f\left( a+b-x \right) } dx$ , the integral becomes

$2\int _{ 0 }^{ \frac { \pi }{ 2 } }{ { \arcsin { \left( \sin { \left( x \right) } \right) } }^{ 2 } } dx$ $=2\int _{ 0 }^{ \frac { \pi }{ 2 } }{ { x }^{ 2 } } dx$ $=\frac { { \pi }^{ 3 } }{ 12 }$ $\approx 2.58385639$

I just numerically integrated using the midpoint rule with 9999 rectangles. Here is my code in Python 3:

https://repl.it/@PhysicsAndMath/Numerical-integration-Midpoint-Rule

If you enter the bounds of integration (pi,0) and set it to maximum accuracy (9999 rectangles), you will get the answer.