Integrating Cosecant
I 1 I 2 = = ∫ csc x d x = ∫ csc x − cot x csc x ( csc x − cot x ) d x = ln ∣ csc x − cot x ∣ ∫ csc x d x = ∫ csc x + cot x − csc x ( csc x + cot x ) d x = − ln ∣ csc x + cot x ∣
If both calculations above are correct, then I 1 and I 2 differ by a constant. Find I 1 − I 2 .
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The difference of two integrals of the same function is a constant, not necessarily a zero. Your "solution" is not correct.
Log in to reply
As you can see from the problem the constant "C" is not mentioned too. According to the problem we may have the two integrals equal.
Log in to reply
See my addition to solution for an example of why it's not obvious that two integrals of the same function are the same.
Log in to reply
@Marta Reece – That's a nice bit of work I admire, The fact is ∫ c o s e c x d x = l n ∣ c o s e c x − c o t x ∣ + C , but the problem statement has assumed C to be zero. Check your problem there's no mention of a constant when you integrate the function in two different forms. It is zero only since your problem makes it seem zero else we can't define such a difference between two integrals as their answer is a family of solution.
Log in to reply
@Aditya Narayan Sharma – With the constant, and the constant being arbitrary, every correct solution is equal to any other correct solution. Therefore I had to leave the constant out. That means I was posting a particular, not a general, solution. Particular solutions may differ by a constant. I was asking what this constant is in this particular case. It happens to be a zero, but that was not a foregone conclusion. It did not follow from the fact that the constant of integration was left out.
I 1 − I 2 = = ln ∣ csc x − cot x ∣ + ln ∣ csc x + cot x ∣ = ln ∣ ( csc x − cot x ) ( csc x + cot x ) ∣ ln ∣ ( csc 2 x − cot 2 x ) ∣ = ln 1 = 0
The solution proper ends here. What follows is for those who do not believe that two integrals of the same function may be different. The text has been placed here only because I am not able to put a picture into a comment.
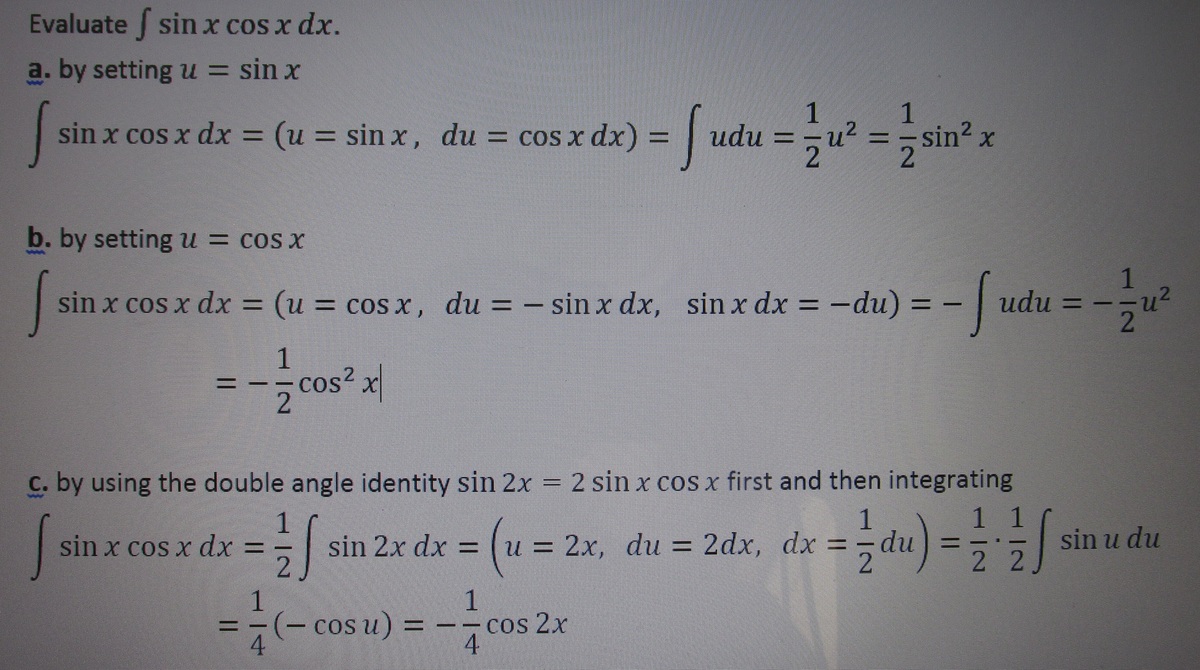
Here are they graphed.
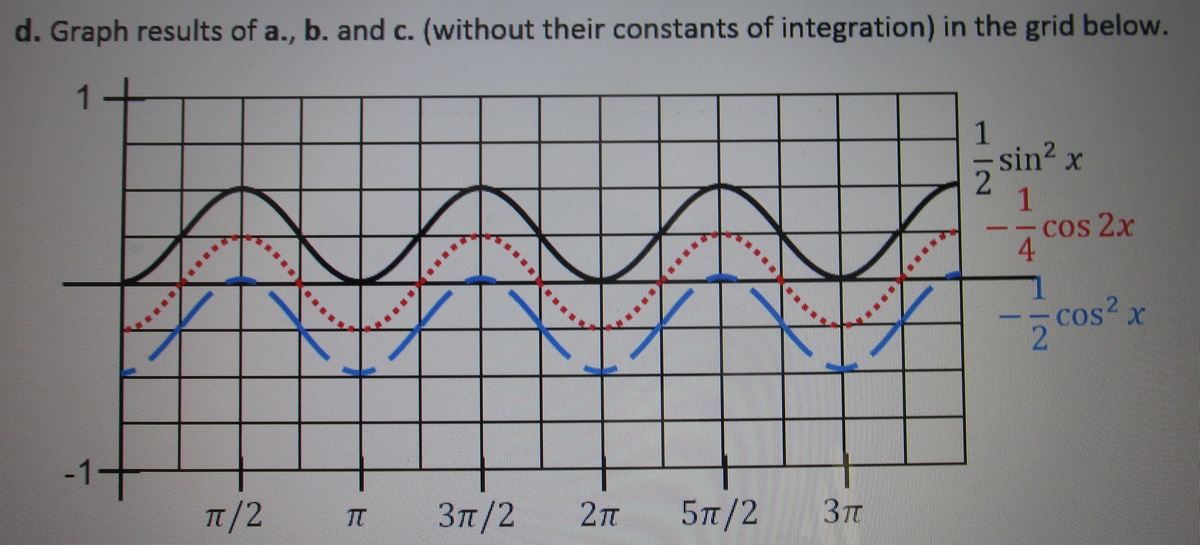
Simply we see I 1 = I 2 , It's obvious ∫ c s c x d x − ∫ c s c x d x = 0