Interaction between a point charge and a ring
A point charge q = + 1 μ C with mass M = 3 g is placed at the center of a thin ring of radius R = 1 0 cm , mass m = 6 g , and charge Q = 5 μ C . Initially, the system is at rest in equilibrium. Then, the point charge is given a push so that it acquires a small velocity v 0 in the plane of the ring. Determine the minimum time τ in seconds after which the point charge will be at the center of the ring again. Assume that the charge in the ring is distributed uniformly. The following expansion might be useful: 1 + R 2 x 2 − 2 R x cos ( θ ) 1 ≈ 1 + cos ( θ ) R x − 2 1 − 3 cos 2 ( θ ) R 2 x 2 for x ≪ R .
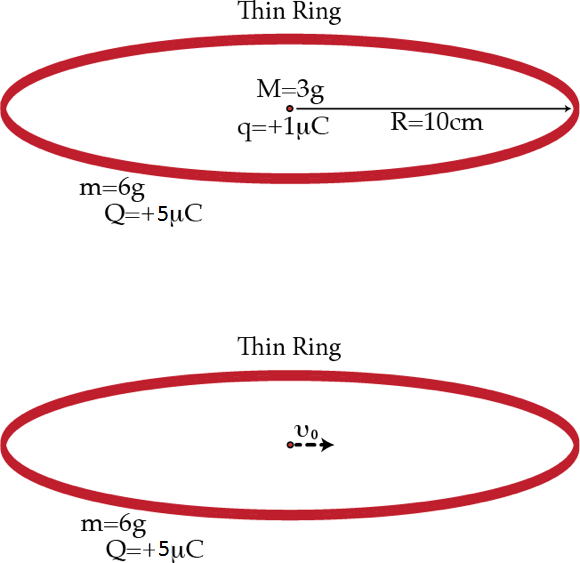
Details and assumptions
-
k = 4 π ϵ 0 1 = 9 × 1 0 9 m/F .
-
Neglect gravitational forces.
-
The ring is free to move.
The answer is 0.0296.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Near the ending,
I haven't mentioned that the oscillations are
simple
harmonic, and what follows apply only to these oscillations.
EDIT:
Also, there is
typo
. In the end, I have written the value of
w
as the inverse of what it should be.
Hence,
Actual
w
=
2
M
m
R
3
K
Q
q
(
M
+
m
)
What follows after that, is correct..
Log in to reply
Dude i really appreciate ur thinking.. Quite good :) Can u help me wid one question dat was posted on brilliant itself long ago(i guess abt 11months ago)? Can i mail u or should i type it in here??
Log in to reply
It would be better if you mail me, so that I won't have to post a solution in the comments section.
Or, just post the link to the problem here and I'll attempt it and post a solution there itself.
[email protected].
Log in to reply
@Anish Puthuraya – K; thx i'll be mailing u soon enough..
Just to be clear, while using reduced mass (mu)*a=kx , a is( a relative), right?
why did u use reduced mass concept? pls explain.
Log in to reply
Because both the ring and the particle are movable Like a 2 block-spring system
In the reference frame fixed to the system's centre of mass O, with x is the distance between point charge and centre of the ring, the distance from O to point charge: d {1}=x\frac{m}{M+m} centre of the ring: d {2}= x\frac{M}{M+m} Thus kinetic energy of each object is given by: K {1}= \frac{1}{2}M(d' {1})^ =\frac{1}{2}\frac{Mm^2}{(M+m)^2}x'^2 K {2} = \frac{1}{2}m(d' {1})^ =\frac{1}{2}\frac{mM^2}{(M+m)^2}x'^2 Interaction energy of system: (p is the linear charge density) W=\int\limits 0^{2\pi}{\frac{kqpRd\theta}{\sqrt{R^2+x^2-2Rxcos\theta}} =\int\limits 0^{2\pi}kqp (1+cos\theta\frac{x}{R}+ \frac{1+3cos^2\theta}{2}\frac{x^2}{R^2})d\theta = kqp(2\pi + \frac{\pi}{2}\frac{x^2}{R^2}) Law of energy conservation: W+K {1}+K {2} =const take derivative: \frac{kqp\pi}{R^2}x+\frac{Mm}{M+m}x''=0 the required time is half a revolution \tau=\pi\sqrt{\frac{mMR^2}{kqp(M+m)\pi}}=\pi\sqrt{\frac{2MmR^3}{kqQ(M+m)}}=0.0296s
It is a fairly interesting problem, so I will try to be as clear as I can.
∙ At a general position x (very small),
Consider a Gaussian surface, which is a cylinder of height 2 ℓ and radius x .
∙ Let E represent the Electric Field at the curved surface of the cylinder ( E ) is constant as x is small)
∙ Let E ′ represent the Electric Field at the two flat surfaces of the cylinder ( E ′ ) is constant as x is small)
Considering the total Flux through the two flat surfaces of the cylinder,
ϕ 1 = 2 × ( E ′ × π x 2 )
As we know,
E ′ = ( R 2 + ℓ 2 ) 2 3 k Q ℓ ≈ R 3 k Q ℓ
Hence,
ϕ 1 = R 3 2 π k Q x 2 ℓ
Considering the total flux through the curved surface of the cylinder,
ϕ 2 = E × 2 π x ( 2 l )
ϕ 2 = E × ( 4 π x l )
Using Gauss's Law ,
ϕ 1 + ϕ 2 = ϵ o q i n s i d e = 0 (Since there is no charge inside the Gaussian surface)
Hence, R 3 2 π k Q x 2 ℓ = − E × ( 4 π x l )
⇒ ∣ E ∣ = 2 R 3 k Q x
F = q E = 2 R 3 k Q q x = K x (say)
Thus,
K = 2 R 3 k Q q
Using the concept of Reduced Mass ,
Reduced Mass = μ = M + m M m
It is clear that,
a = μ K x = w 2 x
Thus,
w = μ K = K Q q ( M + m ) 2 M m R 3
⇒ T = w 2 π = 2 π K Q q ( M + m ) 2 M m R 3
The problem clearly asks us to find out 2 T , thus,
T ′ = 2 T = π K Q q ( M + m ) 2 M m R 3 ≈ 0 . 0 2 9 6 s e c