This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
this problem is in math lesson of nine grade in vietnam :v
Log in to reply
Yeah. It's a 9th standard problem in India too. :3
Log in to reply
Really I was not taught altitude theorem then
Log in to reply
@Ashish Yadav – This is not exactly a theorem. Infact, in Nepal it is considered as a solving method where you have to show the full process using similarity between triangles.
Ask them to do it again in 50 yrs time! I am attempting these to keep my brain active. 63 yr old.
I didn't think i can encounter a genius man like you! Thumbs up! I stared at the problem for20 minutes and cannot devise a solution like yours. Thanks.
Log in to reply
nothing grest bro....all we did'nt remember is the "theorem stuff"......isn't it?????
right angle altitude theorem, we can write AH2=BH*CH........???
Log in to reply
Not really a "theorem". You don't need to memorize it either. Triangle AHC and BHA are similar. He just equated sinA in AHC and sinB in BHA.
This is not explained in details in his solution, but if "O" will be point marking the middle of the circle, then angle ∠BAC, which touches the circle (and is constructed on an arc BC), have half the degrees of the angle constructed on the same arc, but coming from the middle of the circle, that is ∠BOC. Because ∠BOC have 180 degrees, then ∠BAC have 90 degrees, i.e. it's a right angle.
Now, all you need for |AH|^2 = |BH|*|HC| is Pythagorean theorem, used three times. You have that
|AB|^2 + |AC|^2 = (|BH|+|HC|)^2 = |BH|^2 +2|BH||HC| + |HC|^2
Because
|BH|^2 = |AB|^2 - |AH|^2
|HC|^2 = |AC|^2 - |AH|^2
then putting it into previous equality, we get
0 = 2|BH||HC| - 2 |AH|^2
|AH|^2 = |BH||HC|
Hi, is the right angle theorem a scalar product or a simple multiplication between vector lengths??
Log in to reply
no vector dear, he just equated showed ABH and AHC triangles similar and equated the ratios of the sides.
Nice solution. (y) ... though one particular point led me to think, that the solution is purely based on a particular assumption. The lines having segments 6 units and 4 units are diameters of the large circle indeed, but, it was never said in the problem that those two diameters are perpendicular to each other...we assume that, and solve the problem. @Banti Paswan please , have a look.
Log in to reply
Well, you're right to state I did not prove that the diameters are perpendicular. I actually don't think it matters, but I can give a brief explanation as to why that is.
The upper side of the square is, by definition, tangent to the circle (if it isn't it renders our problem pretty much unsolvable). Therefore, the radius drawn from the center of the circle to the tangent point creates a right angle there. But since the upper right corner of the square also forms a right angle, these lines drawn are parallel.
A similar argument can be made to prove that the diameter that crosses the left and right sides of the square also forms a 90 degree angle at the tangent point, which leaves us with no option but to conclude that the last remaining angle in the quadrilateral formed by one of the square's corners, two non-opposing tangent points and the circle's center is 90 degrees. Since all angles are 90 degrees, and two non-opposing sides have the same length, we have a square, and we can safely proceed with the fact that the angle is indeed 90 degrees.
visually, the red line of 4 is NOT half of the distance to H, so 16 cannot be correct as that is drawn
IF line 4 is equal to AH, then that may be the correct solution..as drawn, it clearly is not
The very 1st assumption that ABC is a right triangle . Is invalid
Log in to reply
Sorry. ABC would be inscribed in a semicircle with the diameter as the hypotenuse. ABC absolutely IS a right triangle.
You can really just use estimation that if the line on the left is 3/4 if he way to the middle and the top line is 1/2 that it would naturally be 8 from the top/sides to the middle so then you double that to get 16 and square it
I had never heard of this right angle theorum until now. So any time you take two points at opposite ends of the diameter line of a circle, any third point on the circumference will form a right angle with them? Is there a specific name of this theorum so I can look it up?
I don’t think this is correct either
This is all theoretical maths. The actual diagram is incorrect as the 4 should be 3.8 and the area of the large square is 324. I've drawn it in AutoCAD and the figures shown are impossible.
Log in to reply
I don't know how you drew it in Autocad. There isn't enough information to draw the figure without solving it. Rather than repeat the proof, consider, from hindsight, the location of the center of the small circle, P. From the proof, it is 5 units away from the point C, and 5 units away from the point B. Since the diameter of the large circle is 16, that means point H is 3 units away from the point P. We require that the point A be on the small circle, so it must be 5 units away from the center, P. Then, it is clear that triangle PHA is a 3-4-5 right triangle. Thus, the point A is 4 units from both the center and the edge. This confirms the legitimacy of the math. I will agree that, as is often the case, the drawing is not to scale. But the measurements specified are all consistent. If that's not enough, triangles HBA, HAC, and ABC are all similar, and BH:AH::AH:CH::BA:CA, or 2:4::4:8::2root5:4root5. BH = 2, AH = 4, and CH = 8.
Drawing it in autocad is also theoretical math. In order for you to say 4 is incorrect you need to say the 6 alone (along with the rough shape) is enough to determine the lengths. But it isn't. Instead you need to assume that the distance measured from the centre of the larger circle/square is the same to the centre of the smaller circle as it is to the edge of the smaller circle, i.e. that the radius of the smaller circle is 6.
But no where is that indicated.
(unless you are trying to suggest the shape was drawn perfectly above so you can just measure it with a ruler, but that isn't what you have).
can you wxplain this process in a easier way please....????/
Log in to reply
This is the easiest.What are you talking about?
AO = y-4 = (x+3) -4 = x-1, use Pythagoras (x-1)^2 + 3^2 = x^2 , x^2 -2x +1 +9= x^2, 2x=10, x=5 , y=5+3=8. 16^2=256 Just neatens up your solution method!
Unique and nice way
Nice solution. (y) ... though one particular point led me to think, that the solution is purely based on a particular assumption. The lines having segments 6 units and 4 units are diameters of the large circle indeed, but, it was never said in the problem that those two diameters are perpendicular to each other...we assume that, and solve the problem. @Banti Paswan , please , have a look.
Log in to reply
The diameters are perpendicular to adjacent sides of a square, so they must be perpendicular to each other
FAB.........
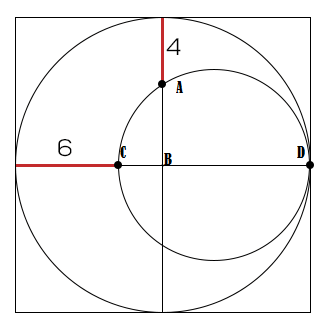
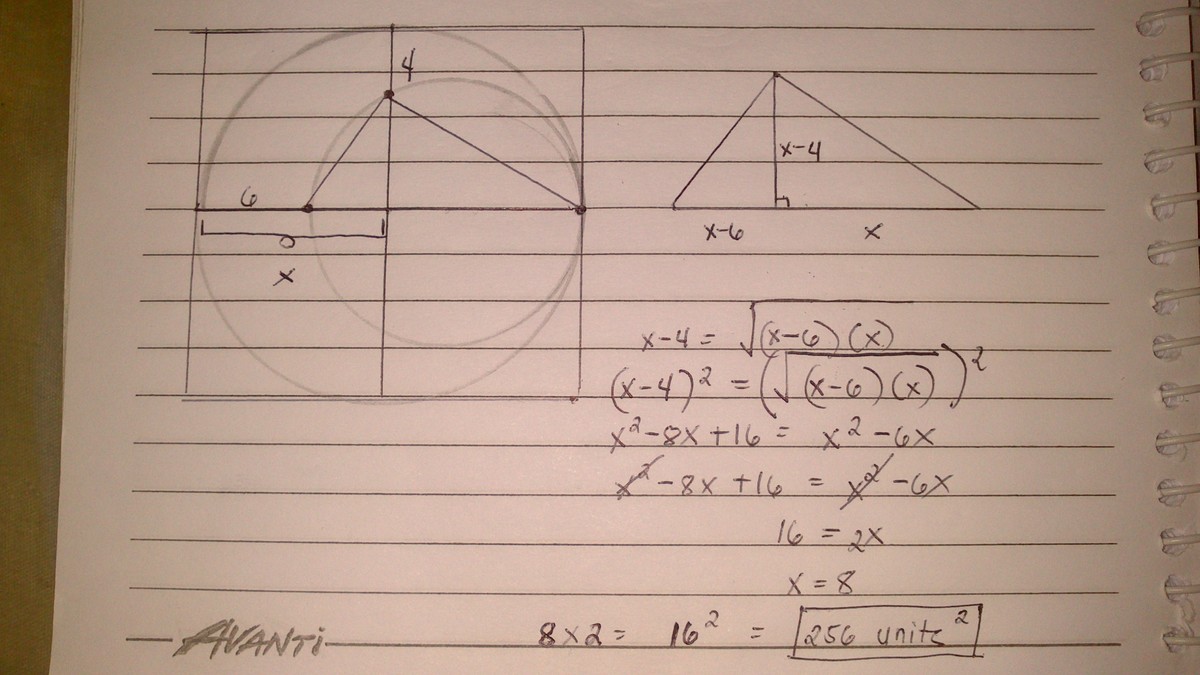
Let x radii of the biggest circunference.
We have that C B = x − 6 and A B = x − 4 . Now △ A C D and A B is its heigth so △ A B C ∼ △ D B A .
A B C B = B D A B
x − 4 x − 6 = x x − 4
x 2 − 6 x = x 2 − 8 x + 1 6
2 x = 1 6
x = 8
Side of the square is equal to 2 x ∴ side longitude is 1 6 ⇒ area is 2 5 6
Nicely done.
m(CAD)=90 Öklid teoremi
Very elegant!
The relationship of the triangles is a neat method. Thanks.
This is the best and easiest to understand. Thanks
For circumference I think you meant circle.
Handwriting is somehow much easier to read than printed text. Very clear to follow.
Let the center of the large circle be O and its radius be r
Let the contact point of the two circles be A
The horizontal diameter of the large circle cuts the small circle at C
The vertical diameter of the large circle cuts the small circle at B above the
horizontal diameter
In the small circle
AC is a diameter
Then
angle ABC is right
In the right triangle ABC
Since BO is perpendicular to AC
Then
(BO)^2 =OA X OC
(r - 4)^2 = r (r - 6)
r = 8
The area of the large square = 16^2 = 256
Let x be the radius of the large circle. Then connect the three points shown to make a triangle. By using the Pythagorean theorem we have the following equality. [(x-6)² + (x-4)²] + [(x-4)² + x²] = [(x-6)+x]² => x = 8 so area of large square is (2x)² = 16² = 256 sq units
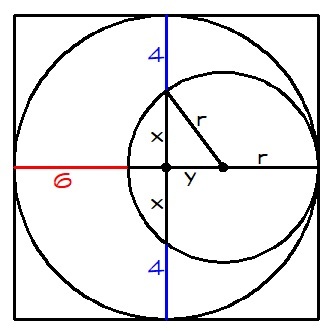 r
+
y
=
2
2
r
+
6
r
+
y
=
2
2
r
+
6
2 r + 2 y = 2 r + 6
2 y = 6
y + 3
2 r + 6 = 8 + 2 x
2 r + 2 + 2 x
r = 1 + x ( 1 )
By the pythagorean theorem, we have
r 2 = x 2 + y 2 ( 2 )
⟹ Substitute y=3 and equation ( 1 ) in ( 2 )
( 1 + x ) 2 = x 2 + 3 2
1 + 2 x + x 2 = x 2 + 9
1 + 2 x = 9
2 x = 8
x = 4
Therefore the area of the big square is four times the area of the small square, we have
A = 4 ( 4 + x ) 2 = 4 ( 4 + 4 ) 2 = 4 ( 6 4 ) = 2 5 6
This is my own solution. This is my deactivated account.
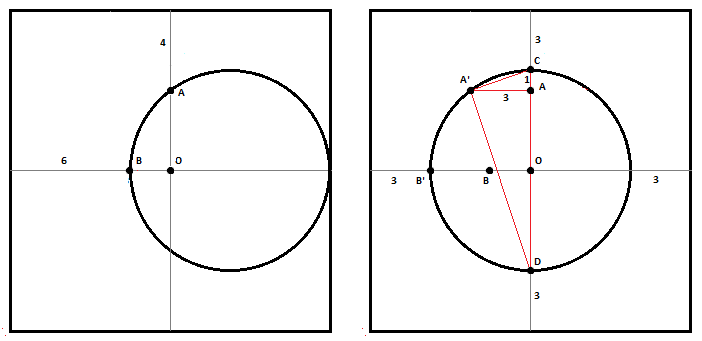
The diagram on the left shows the problem as stated. The large circle is irrelevant and was omitted. Point O is at the center of the square. Point A is where the circle intersects the y-axis above and point B is where the circle intersects the x-axis to the left. The diagram on the right shows the circle re-positioned such that it is now centered on point O. Points C and D represent the upper and lower intersections between the circle and the y-axis. Line CD also represents the diameter of the circle. Points A' and B' represent the same points on the circle which now lie in new locations within the square. Triangle CAA' is a right triangle with legs of CA=1 and AA'=3. Since line CD is the diameter of the circle, angle CA'D must be a right angle. Thus, by the Pythagorean theorem, DA * AC = 3^2, so DA * 1 = 9, thus DA = 9. Therefore the diameter of the circle (line CD) is 10. Thus, the length of a side of the square is 16 and the area of the square is 256. In my initial solution, I defined a triangle with vertexes at C, O, and the midpoint of CA'. Then I used trig to find the radius (CO) of the circle. As I was writing that up, I noticed I could use Pythagoras instead.
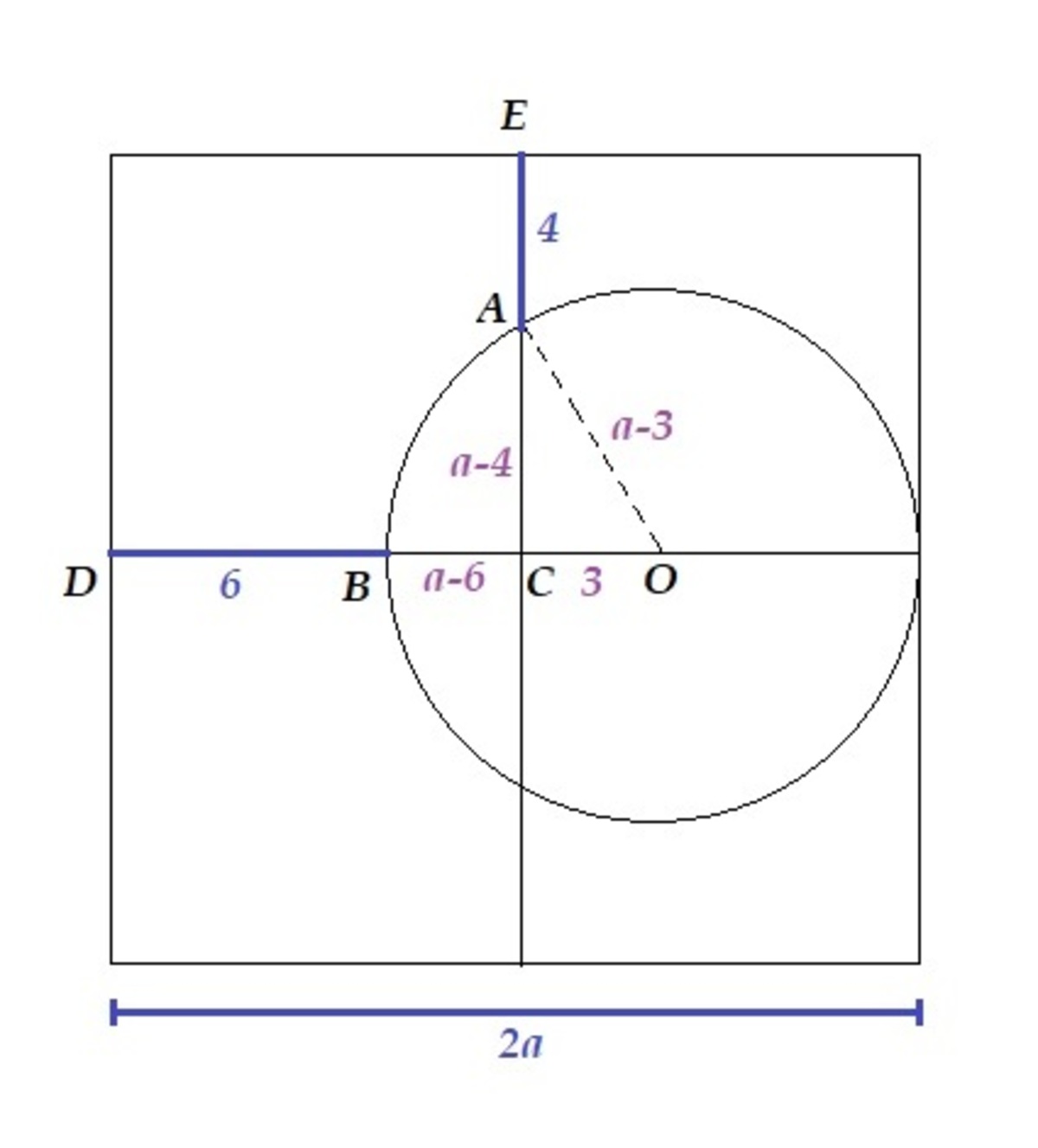
I didn't include the larger circle in the image because it is irrelevant. Let the square be of side: 2 a , with its surface area being 4 a 2 .
The radius of the circle is: 2 2 a − 6 = a − 3 ⇒ O B = O A = a − 3 .
O C = O B − B C = ( a − 3 ) − ( a − 6 ) = 3
O A 2 = A C 2 + O C 2 ⇒ ( a − 3 ) 2 = ( a − 4 ) 2 + 9
a 2 − 6 a + 4 = a 2 − 8 a + 1 6 + 9 ⇒ a = 8 ⇒ A = 2 5 6
By looking at the diagram, you can see that the line of length 4 divides the height of the small square into 2. So, the height of the side of the small square is 8. So the area of the small square is 64. As there are 4 such squares, the total area is 256. It really is a lot about intuition. Not a very recommended method but fast.
Since the line of 4 is half of the smaller square therefore 8 is the total height and base if the smaller square. 8 * 8= 64 and since there are 4 squares 64 * 4= 256
Using notation as below and assuming r as the radius of the small circle: Diameter of large circle = CB + 8 = 2r + 6. So radius of large circle = CH = r + 3. BH = (r + 3) - 6 = r - 3. AH = HD = (r + 3) - 4 = r - 1 (assuming D is the intersection of AH produced on the small circle). But AH HD = BH HC. So (r + 3) (r - 3) = (r - 1) (r - 1) Solving for r, we have r = 5. So diameter of the large circle = 2r + 6 = 16 and area of the large square = 256.
The diameter of the large circle is 2s where s is the unknown side half-length of the large square. This makes the diameter of the small circle 2s -6 and then the radius s - 3 and if the central lines cross at the origin of a Cartesian coordinate system, the small circle has two x-intercepts: (s, 0) and (-s + 6, 0) and thus has center ( (s + -s + 6)/2, 0 ) or (3,0)
This makes the equation of the smaller circle
(x - 3)^2 + y^2 = (s -3)^2
We know some points on the circle, like the uppermost y-intercept (0, s-4)
Plug that in for x = 0 and y = 4 and solve for s = 8
The square has sides 2*s = 16 and area s^2 = 256.
Nice puzzle!
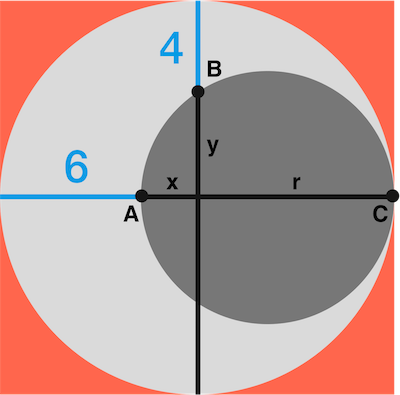 A
B
C
is a
right triangle
. Therefore
A
B
2
+
B
C
2
=
A
C
2
.
A
B
C
is a
right triangle
. Therefore
A
B
2
+
B
C
2
=
A
C
2
.
Express the Pythagorean identity in terms of x , y and r : ( x 2 + y 2 ) + ( y 2 + r 2 ) = ( x + r ) 2 .
Simplify to get y 2 = x ⋅ r
Substitute x = r − 6 and y = r − 4 to get ( r − 4 ) 2 = r ( r − 6 ) ⟹ r 2 + 1 6 − 8 r = r 2 − 6 r ⟹ r = 8 .
The area of the large square is then 4 r 2 = 2 5 6 .
I’m probably the only person who solved it with pixel measurements lol
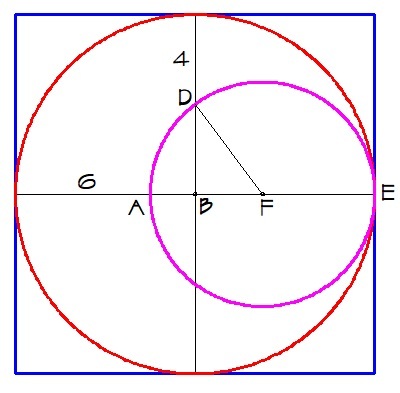 6
+
A
B
=
4
+
B
D
⟹
B
D
=
2
+
A
B
or
A
B
=
B
D
−
2
6
+
A
B
=
4
+
B
D
⟹
B
D
=
2
+
A
B
or
A
B
=
B
D
−
2
B C = 2 2 F D + 6 = F D + 3
F D + 3 = 4 + B D ⟹ F D = B D + 1
B F = F D − A B = B D + 1 − ( B D − 2 ) = B D + 1 − B D + 2 = 3
Using pythagorean theorem, we have
F D 2 = B D 2 + B F 2
( B D + 1 ) 2 = B D 2 + 9
B D 2 + 2 B D + 1 = B D 2 + 9
2 B D = 8
B D = 4
So the radius of the big circle is 4 + 4 = 8 .
Thus, the area of the square is 1 6 2 = 2 5 6 .
The figure looks to scale. So what I did was look at the smaller inside squares instead of the circles. It looks like they have side lengths of 8, making the bigger squares side lengths 16. A = l X w. 16 X 16 = 256.
If you compare 4 and 6 you end up 8 as your small square size double to 16 multiply by 2 and there's your answer of 256 without all the head racking


I've labeled a few points of interest in the figure, which will be showcased here: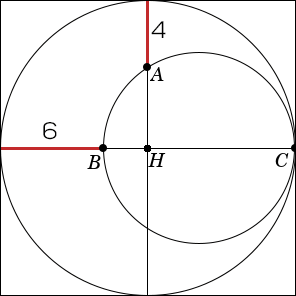
Since B C is the diameter of the small circumference, and A is a point within the circumference itself, then A B C is a right triangle. Furthermore, A H is perpendicular to B C , thus A H is the altitude of the triangle with respect to the hypotenuse.
Let R be the radius of the large circumference. Thus, it is obvious that the following segments measure, respectively:
A H = R − 4
B H = R − 6
C H = R
From the right angle altitude theorem, we can write: A H 2 = B H ∗ C H
Then:
( R − 4 ) 2 = R ∗ ( R − 6 )
R 2 − 8 R + 1 6 = R 2 − 6 R
2 R = 1 6
R = 8
Since the side of the square is equal to the diameter of the large circle, then its side is 1 6 ; thus, the area equals 1 6 2 = 2 5 6