Thought of using Maclaurin series to expand log(1+x) but it was too long then I took to this solution.
First substitute x = $tan\theta$ , then limits of intregral would be in terms of $\theta$ .
Now $tan^{-1}x$ = $\theta$ . Therefore the limits would become $tan^{-1}(1)$ and $tan^{-1}(0)$ which would be $\frac{\pi}{4}$ and 0 respectively.
In my solution all the log are to the base e.

$\begin{aligned} x&= tan\theta\\ dx&= sec^{2}\theta d\theta \end{aligned}$

Then the intregral would become

$\begin{aligned} Q&= 8\int_{0}^\frac{\pi}{4} \frac{log(1+x)}{1+x^2}dx\\ &= 8\int_{0}^\frac{\pi}{4} \frac{log(1+tan\theta)}{1+tan^2\theta}sec^2\theta d\theta\\ &= 8\int_{0}^\frac{\pi}{4} \frac{log(1+tan\theta)}{sec^2\theta}sec^2\theta d\theta\\ &= 8\int_{0}^\frac{\pi}{4} log(1+tan\theta) d\theta ---> eq 1 \end{aligned}$

Now using $\int_{0}^a f(x)dx$ = $\int_{0}^a f(a-x)dx$ . We get
$\begin{aligned} Q&= 8\int_{0}^\frac{\pi}{4} log(1+tan(\frac{\pi}{4}-\theta)) d\theta\\ &= 8\int_{0}^\frac{\pi}{4} log(1+\frac{tan(\frac{\pi}{4})-tan\theta}{1+tan\theta tan(\frac{\pi}{4})}) d\theta\\ &= 8\int_{0}^\frac{\pi}{4} log(1+\frac{1-tan\theta}{1+tan\theta}) d\theta\\ &= 8\int_{0}^\frac{\pi}{4} log(\frac{2}{1+tan\theta}) d\theta\\ &= 8\int_{0}^\frac{\pi}{4} log2 -log(1+tan\theta) d\theta ---> eq2 \end{aligned}$

Adding eq 1 and 2. We get,
$\begin{aligned} 2Q&= 8\int_{0}^\frac{\pi}{4} log2 d\theta\\ Q&= 4(\frac{\pi}{4}-0)log2\\ &= \pi log2 \end{aligned}$

So the ans is $\frac{\pi}{2}$ = 1.57.

Since nobody used a simple graph, here it is!! First, let's create a graphic representation of our question. To have a graphic using our a and b, substitute them with x and y.

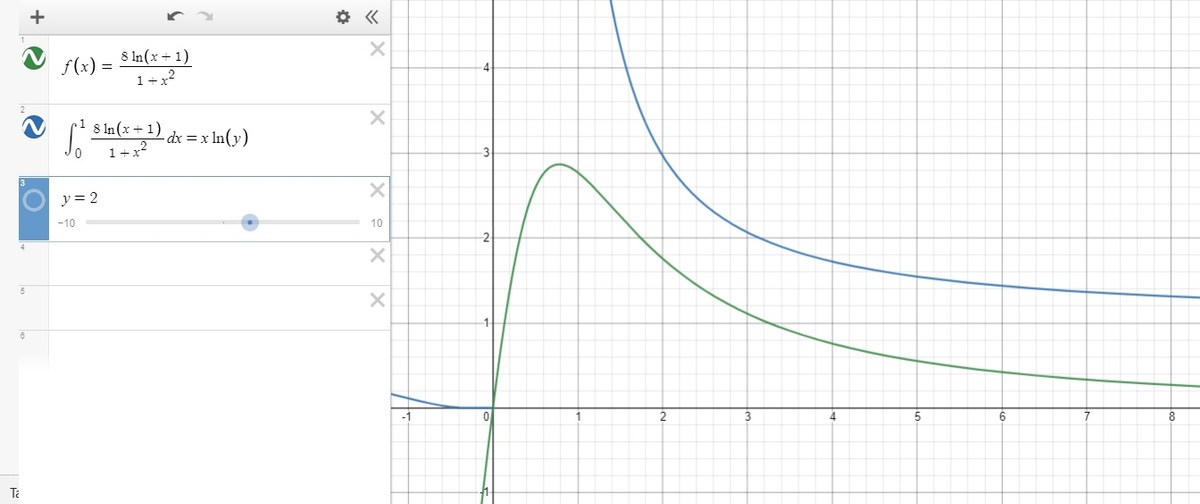
Next, try some prime numbers and which they intersect with a known constant. 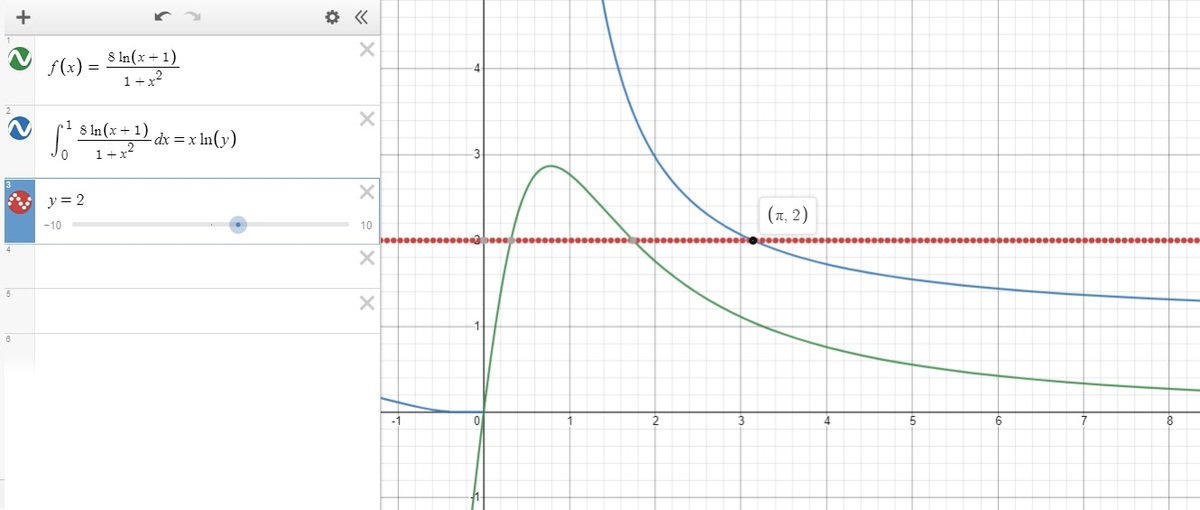So the answer is π/2!!

Okay, so a couple of nice solutions have already been given and in my initial answer I also used the substitution $x=\tan(u)$ .

This is why I wanted to try something a bit "less trigonometric" :) My main goal is to substitute in such a way, that there will be some kind of multiplication or division in the logarithm, so that I can pull it apart while keeping the form of the denominator intact.

Through a LOT of playing around I found the substitution $x=\frac{1-u}{1+u}$ to work. So let me walk you through how the calculation goes.

First, let's do the differentials: $\begin{aligned} x&=\frac{1-u}{1+u}\\ \text{d}x &= -\frac{2}{(1+u)^2}\text{d}u. \end{aligned}$

Now the function arguments: $\begin{aligned} 1+x &= 1 +\frac{1-u}{1+u}=\frac{2}{1+u}\\[10pt] 1+x^2 &= \frac{(1+u)^2+(1-u)^2}{(1+u)^2}=\frac{2(1+u^2)}{(1+u)^2}\quad\mid ()^{-1}\\ \frac{1}{1+x^2} &=\frac{(1+u)^2}{2(1+u^2)}. \end{aligned}$

If we let $I$ be $\frac{1}{8}$ -times our integral, we find $\begin{aligned} I &= \int_0^1 \frac{\ln(1+x)}{1+x^2}\text{d}x\\ x=\frac{1-u}{1+u} \implies I &= -\int_1^0 \ln\left(\frac{2}{1+u}\right)\cdot\frac{(1+u)^2}{2(1+u^2)}\cdot\frac{2}{(1+u)^2}\text{d}u\\ &= \int_0^1 \frac{\ln(2)-\ln(1+u)}{1+u^2}\text{d}u\\ &= \ln(2)\int_0^1 \frac{1}{1+u^2}\text{d}u -\int_0^1\frac{\ln(1+u)}{1+u^2}\text{d}u\\ &= \ln(2)\arctan{1} -I\quad\mid +I\\ 2I &= \ln(2)\cdot \frac{\pi}{4}\quad\mid :2\\ I &= \frac{\pi}{8}\ln(2)\quad\mid \cdot 8\\ 8I &= \pi\ln(2) = a\ln(b)\\ \implies \frac{a}{b} &= \frac{\pi}{2} \approx 1.57 \end{aligned}$

Similar solution with others'

$\begin{aligned} I & = \int_0^1 \frac {8\ln(1+x)}{1+x^2} dx & \small \blue{\text{Let }x = \tan \theta \implies dx = \sec^2 \theta \ d \theta} \\ & = \int_0^\frac \pi 4 \frac {8\ln(1 + \tan \theta)}\blue{1+\tan^2 \theta} \cdot \blue{\sec^2 \theta} \ d\theta & \small \blue {\text{Note that }\sec^2 \theta = 1 + \tan^2 \theta} \\ & = \int_0^\frac \pi 4 8 \ln (1+\tan \theta) \ d\theta & \small \blue{\text{By reflection }\int_a^b f(x) \ dx = \int_a^b f(a+b-x)\ dx} \\ & = 4 \int_0^\frac \pi 4 \left(\ln (1+\tan \theta) + \ln \left(1+\tan \left(\frac \pi 4 - \theta \right)\right) \right) d\theta \\ & = 4 \int_0^\frac \pi 4 \left(\ln (1+\tan \theta) + \ln \left(1+\frac {1-\tan \theta}{1+\tan \theta} \right)\right) d\theta \\ & = 4 \int_0^\frac \pi 4 \left(\ln (1+\tan \theta) + \ln \left(\frac 2{1+\tan \theta} \right)\right) d\theta \\ & = 4 \int_0^\frac \pi 4 \left(\ln (1+\tan \theta) + \ln 2 - \ln (1+\tan \theta) \right) d\theta \\ & = 4 \int_0^\frac \pi 4 \ln 2 \ d\theta = 4 \theta \ln 2 \ \bigg|_0^\frac \pi 4 = \pi \ln 2 \end{aligned}$

Therefore $\dfrac ab = \dfrac \pi 2 \approx \boxed{1.57}$ .

$I=\int_0^1 \dfrac{\ln(1+x)dx}{1+x^2}$ $let\space x=\tan u\Rightarrow dx=\sec^2u du$ $\Rightarrow I=\int_{x=0}^{x=1}\dfrac{\ln(1+\tan u)\cancel{\red{\sec^2u}}du}{\cancel{\red{1+tan^2u}}}$ $I=\int_{u=0}^{u=\frac{\pi}{4}}\ln(1+\tan u)du..........[1]$ $=\int_{0}^{\frac{\pi}{4}}\ln(1+\red{\tan(\frac{\pi}{4}-u)})du \space\blue{\because \int_{0}^a f(x)dx=\int_0^a f(a-x)dx}$ $=\int_{0}^{\frac{\pi}{4}}\ln(1+\red{\dfrac{1-\tan u}{1+\tan u}})du$ $=\int_{0}^{\frac{\pi}{4}}\ln(\dfrac{2}{1+\tan u})du$ $=\int_{0}^{\frac{\pi}{4}}\ln(2)du-\int_{0}^{\frac{\pi}{4}}\ln({1+\tan u})du$ $=\dfrac{\pi\ln 2}{4}-\int_{0}^{\frac{\pi}{4}}\ln({1+\tan u})du..........[2]$ $[1]\space and \space [2]\Rightarrow \red{\int_{0}^{\frac{\pi}{4}}\ln(1+\tan u)du}=\dfrac{\pi\ln 2}{4}-\red{\int_{0}^{\frac{\pi}{4}}\ln({1+\tan u})du}$ $\Rightarrow \red{I}=\dfrac{\pi\ln 2}{4}-\red{I}$ $\Rightarrow 8I={\pi\ln 2}$ $\Rightarrow \boxed{\int_0^1 \dfrac{8\ln(1+x)dx}{1+x^2}={\pi\ln 2}}$ $\Rightarrow a=\pi, b=2$ $\Rightarrow \dfrac{a}{b}=\dfrac{\pi}{2}\approx 1.5707...$

$\blue{Proof\space of\space blue\space statement:}$ $I=\int_{0}^a f(a-x)dx$ $let \space u=a-x\Rightarrow dx=-du$ $\Rightarrow I=-\int_{x=0}^{x=a} f(u)du$ $=-\int_{u=a}^{u=0}f(u)du=\int_{0}^af(u)du$ $=\int_0^a f(x)dx$ $\Rightarrow \int_{0}^a f(a-x)dx=\int_0^a f(x)dx$

$\textcolor{#69047E}{8*∫^{1}_{0}\frac{ln(1+x)dx}{1+x^{2}}=alnb}$

Since we don't have any direct method to integrate logarithmic functions ,we do so by substituting appropriate values in them

Note : the substitution made should be such that it can break the above equation into a function and its derivative.

In the above case ,this can be achieved by substituting $\boxed{\textcolor{#20A900}{x=tanθ}}$

Differentiating both sides we get,

$\textcolor{#CEBB00}{dx=sec^{2}θdθ}$ .

Since $\frac{d(tanθ)}{dθ}$ = $sec^{2}θ$

---

$\textcolor{#69047E}{8*∫^{1}_{0}\dfrac{ln(1+tanθ)sec^{2}θdθ}{1+tan^{2}θ}}$

---

$\textcolor{#20A900}{Cancelling( 1+tan^{2}θ) and( sec^{2}θ)}$

Since, $1+tan^{2}θ$ = $sec^{2}θ$

We get

$\textcolor{#69047E}{8*∫^{1}_{0}ln(1+tanθ)dθ}$

The variables are now in terms of theta and not in terms of x ,so we will have to find the corresponding upper limit and the lower limit of the function by substituting 1 and 0 respectively in x .

When x=0,tan(θ)=0=tan0°

$\textcolor{#D61F06}{0---[LOWER‿LIMIT]}$

When x=1,tan(θ)=1=tan $\frac{π}{4}$

$\textcolor{#D61F06}{\frac{π}{4}----[UPPER‿LIMIT]}$

Let $\textcolor{#69047E}{8*∫^{\frac{π}{4}}_{0}ln(1+tanθ)dθ}$ be = $\boxed{T}$

Using the property of definite integrals : $\boxed{∫^{a}_{0} f(x)=∫^{a}_{0}f(a-x)dx}$

Therefore, $T$ = $\textcolor{#69047E}{8*∫^{\frac{π}{4}}_{0}ln(1+tan\frac{π}{4}-θ)dθ}$ -------- $\boxed{✿}$

---

Since tan(a-b)= $\frac{tana-tanb}{1+tanatanb}$

---

$⇒$ $T=\textcolor{#69047E}{8*∫^{\frac{π}{4}}_{0}ln1+\dfrac{1-tanθ}{1+tanθ}dθ}$

$\boxed{tan\dfrac{π}{4}=1}$

---

$⇒$ $T=\textcolor{#69047E}{8*∫^{\frac{π}{4}}_{0}ln\dfrac{1+tanθ+1-tanθ}{1+tanθ}dθ}$

---

$T=\textcolor{#69047E}{8*∫^{\frac{π}{4}}_{0}ln\dfrac{2}{1+tanθ}dθ}$

---

Since $ln\dfrac{a}{b}=ln a -ln b$

---

$=>$ $T$ = $\textcolor{#69047E}{8*∫^{\frac{π}{4}}_{0}ln(2)-ln(1+tanθ)}dθ$ ---- $\boxed{✪}$

---

Adding $\boxed{✪}$ and $\boxed{✿}$ so that the equation gets reduced to ln 2

---

$2T=$ $\textcolor{#69047E}{8∫^{\frac{π}{4}}_{0}ln 2 d(θ)}$

---

Since $ln 2$ is a constant,

---

$2T=$ $\textcolor{#69047E}{8*ln 2∫^{\frac{π}{4}}_{0}d(θ)}$

---

Since, $∫^{a}_{0}$ dθ = $[θ]^{a}_{0}$

---

$2T=$ $\textcolor{#69047E}{8*ln 2([θ]^\dfrac{π}{4}_0)}$

---

$T=$ $\textcolor{#69047E}{4 *\dfrac{π}{4}*ln 2}$

---

$T=$ $\textcolor{#69047E}{π*ln2=a*lnb}$

---

$T$ = $π*ln2$ = $a*lnb$

---

Comparing the two equations we came to know that ,

$\textcolor{#20A900}{a=π}$

$\textcolor{#20A900}{b=2}$

---

$\textcolor{#69047E}{\dfrac{a}{b}=\dfrac{π}{2}}$

---

Since $π$ =3.14

---

$\dfrac{π}{2}$ = $1.57$

---

Hence $\boxed{\textcolor{turquoise}{1.57}}$ is the correct answer!

$\textcolor{#D61F06}{Warning!}$ Don't even try integrating this function by parts because you will probably be left with

$\boxed{tan^{-1}x*sec^{2}(tan^{-1}x)*\dfrac{1}{2}ln|cos(tan^{-1}x)+sin(tan^{-1}x)|+\dfrac{tan^{-1}x}{2}+2*∫^{\frac{π}{4}}_0[tan^{1}x*sec^{2}(tan^{-1}x)*x]}$

to integrate:(