International Mathematical Olympiad 2 0 1 9 , Day 2 , Problem 4 of 6
Note - Supposed to set this 3 weeks ago but never mind...
Question:
Find all pairs ( k , n ) of positive integers such that:
k ! = ( 2 n − 1 ) ( 2 n − 2 ) ( 2 n − 4 ) ... ( 2 n − 2 n − 1 )
Country that gave the Question: El Salvador
Give your answer as the number of pairs ( k , n ) of positive integers that satisfies the question.
The person that answers this correctly and gives the official solution first - there is 2 - go to International Mathematical Olympiad (IMO) Hall of Fame .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Good solution! Not the official one though... @Alak Bhattacharya .
P.S. I have the official solutions...
Do you have the official solutions? @Hamza Anushath
Log in to reply
Not exactly, but I know the format of how to submit the answers
Why @Yajat Shamji ?
Log in to reply
Oh, just that if anybody (apart from me) has the official solutions and uses it, that's cheating.
Luckily, you don't have them, otherwise...
Log in to reply
@A Former Brilliant Member – Hahaha, if I had them, I would have used them for every question you posted.
Anyway, from where did you get the text from? I thought the solution were a big book, not a PDF?
Log in to reply
@A Former Brilliant Member – It's a PDF...
I didn't know how to type some symbols in latex, so I typed them somewhere else and took a screenshot
Log in to reply
Ok. I will change the date then in the Hall of Fame...
Solution
1
:

 Solution
2
:
Solution
2
:

Ok. I wanted submit the solutions and not the number of solutions.
Oh god, I was just going to post a solution @Yajat Shamji
Log in to reply
Did you not see the Hall of Fame? Last time of submission for solutions for recognition is 2 3 : 5 8 pm on the day of submitting the problem.
Log in to reply
That's true @Yajat Shamji , yet trial is necessary, isn't it?
And wich timezone?
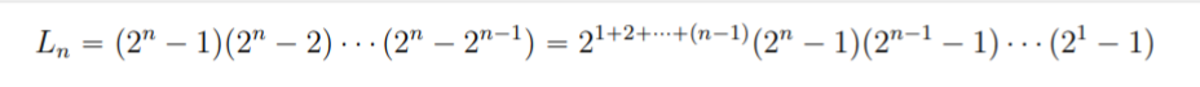
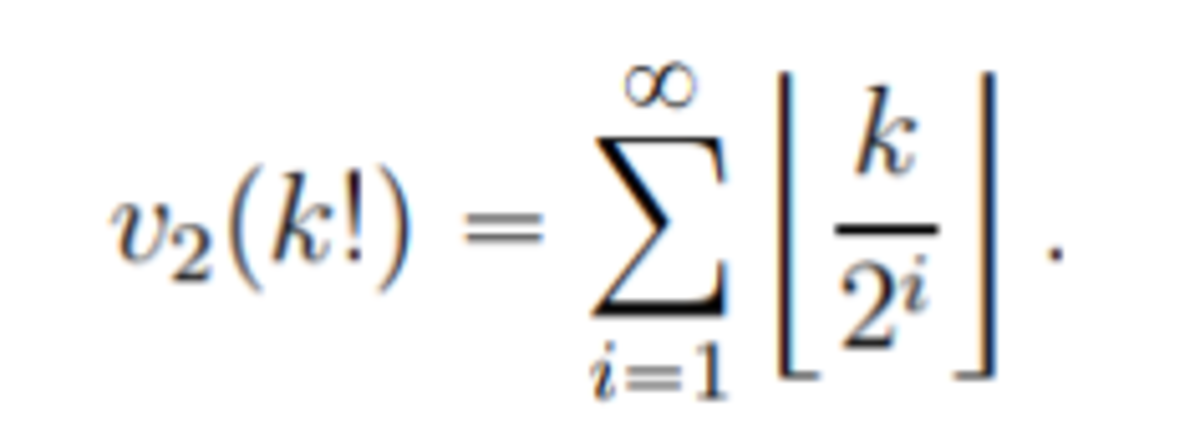
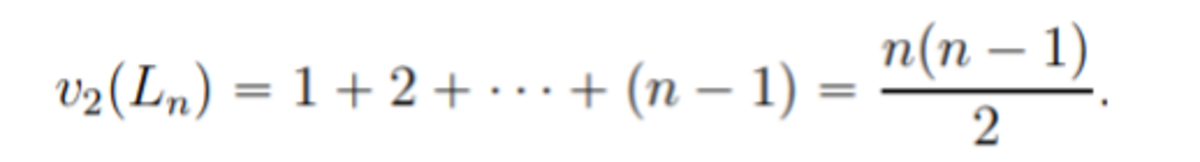

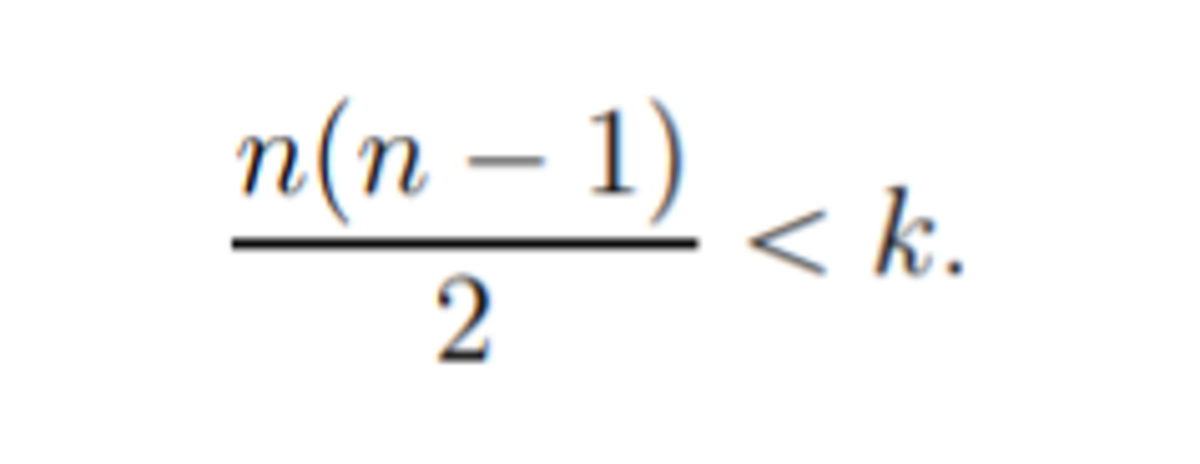
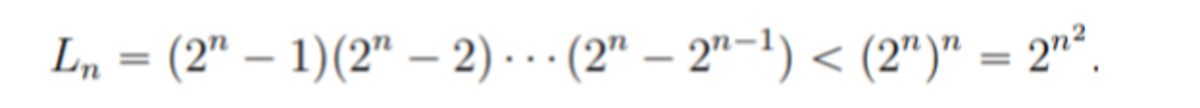
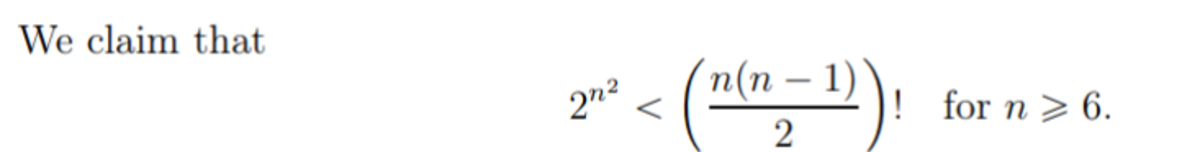
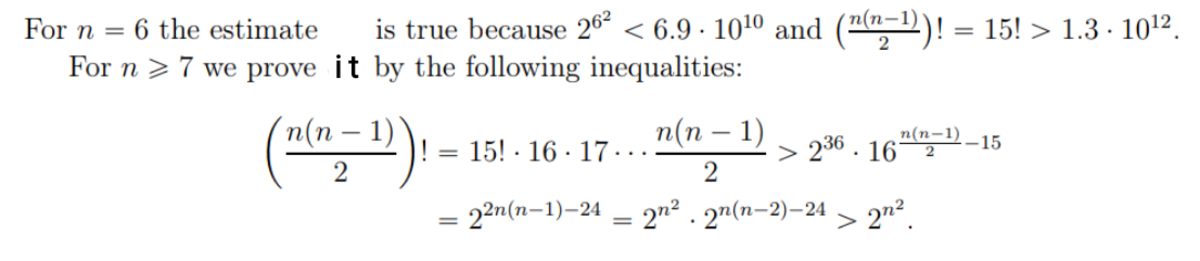
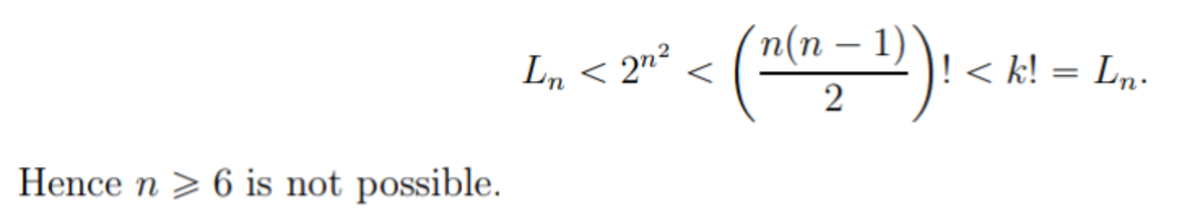
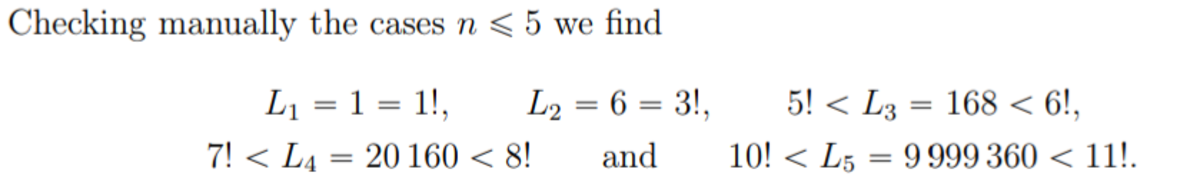

Since for k ≥ 4 all the odd numbers will not be present in the R. H. S. of the identity for any value of n , this side can never be expressed as the factorial of a number. Hence 0 ≤ k ≤ 3 . In this range, only two pairs, namely ( k , n ) = ( 1 , 1 ) and ( 3 , 2 ) exist. So the total number of such pairs is 2