Intersection of two graphs
b is a real number greater than 1 such that the equation x 2 = lo g b x has exactly one real solution.
Submit ⌊ 1 0 0 0 0 { b } ⌋ , where { ⋅ } and ⌊ ⋅ ⌋ denote the fractional part function and floor function , respectively.
The curves only touch once.
The answer is 2019.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
@Henry U I believe your condition isn't sufficient. For example, h ( x ) = x − 2 1 has a unique solution at x = 2 1 and h ′ ( x ) = 1 > 0 , but we do not have h ′ ( x ∗ ) = 0 .
Perhaps what you are going for is if we add that h ′ ( x ) < 0 on [ 0 , x ∗ ) and then assume the continuity of h ′ ?
Can you revisit this and see how to fix it?
@Antoine G I believe your condition isn't sufficient. For example, h ( x ) = e x − k has a unique solution at x = ln k , and h ′ ′ ( x ) = e x > 0 , but h ′ ( x ) = 0 .
Can you revisit this and see how to fix it?
Log in to reply
Well, I also thought about it. The important point is that the function goes to infinity at the boundary of the domain of definition (and not so much the convexity). This positivity is not satsisfied by e x − k : although x → + ∞ lim e x − k = + ∞ , one has x → − ∞ lim e x − k = − k .
So actually, one needs much less than convexity: you only need that the function take positive values (or + ∞ ) at the boundary of its definition domain (which is the case for x 2 − lo g b x ), and it is differentiable.
Indeed, let [ a , c ] be the domain and assume the function has only one zero x 0 and h ′ ( x 0 ) = 0 . Then there are x very close to x 0 so that h ( x 0 ) < 0 . Let x 1 be such a point, then by the intermediate value theorem there are two zeroes: one in the interval [ a , x 1 ] and one in the interval [ x 1 , c ] .
So to sum up: Assume h has domain [ a , c ] (the interval could be half-open or open; a and c could be infinite), is such that x → a lim h ( x ) = > 0 (with + ∞ being considered > 0 ), x → c lim h ( x ) > 0 and h has a derivative everywhere. Then if h has only one zero on [ a , c ] , the derivative of h also has a zero there.
Log in to reply
Right, so that's back to the condition in example 1. It doesn't seem like there are any other (non-equivalent) conditions that work (though I haven't fully investigated this as yet).
Note, it's not fair to say that "positive endpoints is much less than convexity" because neither conditions imply the other, though it's much easier to think of cases where we have positive endpoints without convexity than convex functions without positive endpoints.
Log in to reply
@Calvin Lin – oh, I did not mean "positive endpoints is less than convexity", I meant "continuous + positive endpoints is less than convexity + positive endpoints". Sorry if that was unclear.
Although to be fair this isn't quite true either (since there are non-continuous convex functions, but they are very messy).
Geez that's hard to know.😅😗😖😖😖
It comes as 1 . 2 0 1 9 4 3 3 6 3 3 5 5
Surprisingly, I don't see any solution with Lambert W.
Rewrite the equation as follows:
b x 2 = x e x 2 ln b = x e 2 x 2 ln b = x 2 x 2 e − 2 x 2 ln b = 1 − 2 x 2 ln b ⋅ e − 2 x 2 ln b = − 2 ln b − 2 x 2 ln b = W ( − 2 ln b ) x = − 2 ln b W ( − 2 ln b )
Since b > 1 , ln b > 0 , so − 2 ln b < 0 , and W is multivalued for negatives, except at − 1 / e .
Thus, for the solution to be unique, we must have − 2 ln b = − 1 / e , or b = e 1 / 2 e ≈ 1 . 2 0 1 9 4 .
But Sir please here see the function as here intersection cannot be possible as
The graph of logarithmic
function will "Overtake" the
x^2 graph thus there will be 2
intersections then
Log in to reply
I don't see why there must be 2 intersections. Why can't the curve be tangential? (which is how you get 1 solution)
The equation x 2 = lo g b x can be rewritten as b = x x 2 1 . If we consider the function y = x x 2 1 y ′ = x x 2 1 − 3 ( 1 − 2 ln x ) we see that y takes its maximum at x = e , and the maximum value of y is b = e 2 e 1 . This makes the answer 2 0 1 9 .
Please explain why did we consider maximum value of function y.
Log in to reply
If 1 < b < e 2 e 1 , then there are two values of x > 0 for which x x 2 1 = b . Only by choosing b to be the maximum do we get a single solution to the equation.
The question is equivalent to ask that h ( x ) = f ( x ) − g ( x ) has a single zero. Note that h is a continuous differentiable function on the interval [ 0 , + ∞ [ (since x 2 and lo g b are). Furthermore h tends to ∞ as x → 0 + or x → + ∞ . For a such a function to have a single zero means that h ( x ) = 0 and h ′ ( x ) = 0 (see Lemma below).
h ( x ) = 0 is the equation (I): x 2 − ln b ln x = 0 and h ′ ( x ) = 0 is the equation (II): 2 x − x ln b 1 = 0 .
(II) ⟺ 2 x = x ln b 1 ⟺ 2 x 2 = ln b 1 ⟺ x 2 = 2 ln b 1 .
You can input that in (I): x 2 − ln b ln x = 0 ⟺ 2 ln b 1 − ln b ln x = 0 ⟺ 2 1 = ln x ⟺ x = e .
Now use (II) again: e = 2 ln b 1 ⟺ b = e 1 / 2 e .
Lemma (basically just the intermediate value theorem)
Statement of the Lemma: Assume h has domain [ a , c ] (the interval could be half-open or open; a and c could be infinite), is such that x → a lim h ( x ) = > 0 (with + ∞ being considered > 0 ), x → c lim h ( x ) > 0 and h has a derivative everywhere. Then if h has only one zero on [ a , c ] , the derivative of h also has a zero there.
Proof of the Lemma: Assume the function has only one zero x 0 and that h ′ ( x 0 ) = 0 . Then there are x very close to x 0 so that h ( x 0 ) < 0 . Let x 1 be such a point, then by the intermediate value theorem there are two zeroes: one in the interval [ a , x 1 ] and one in the interval [ x 1 , c ] .
Note that the question didn't state "common point with a common tangent". How do you know that there must be a common tangent?
Log in to reply
Right thanks!
The function f is convex while the function g is concave. This means the function h = f − g is convex. If a convex function has only one zero and it tends to + ∞ at the boundary of its domain, then it must be a zero of [even] degree 2 or more... I'll update.
Log in to reply
Good call about the convexness of h . I've added this as the third condition in my solution.
x 2 = ln b ln x
(Let ln b = c )
The graphs of these two functions will have exactly one solution when they just touch. Thus, not only will the function value be equal but also the value of slope of the tangent at that point (let it have abscissa x 1 )
∴ , f ( x 1 ) = g ( x 1 ) ; f ′ ( x 1 ) = g ′ ( x 1 )
2 x 1 = x 1 c 1
x 1 = 2 c 1
Putting that in the very first equation, we get c = 2 e 1
Hence, b = e 2 e 1 ≈ 1 . 2 0 1 9
Thus, ⌊ 1 0 0 0 0 { b } ⌋ = 2 0 1 9
Listen, can you please post solution to your recent DE problem. I want to improve my DE skills because I am really bad at it, I have been trying your problem but not able to figure out the answer. Please help.
Why is it that "These two curves have exactly one solution implies that they have a common tangent"?
If the question was " b is a real number such that x = b x has exactly one real solution", would your approach of taking derivatives work?
Log in to reply
The way these graphs are designed, where one goes from +∞ to +∞ again, and the other from goes from -∞ to +∞ (from outside the former graph), makes them either always intersect at 2 points, 1 if they just touch, or not intersect at all.
This approach would not work with straight lines, as they are destined to have either 1 or 0 intersection points.
The intersection of f(x) and g(x) gives us a function with 1 or more roots, letting us know they can intersect at multiple points. According to the question, we can make that function have repeated roots, which would make f(x)=g(x) have lesser solutions.
Log in to reply
- The counterexample isn't restricted to "straight lines". Here's an example with curved lines: x 2 + x = x 2 + b x .
The condition about "goes from + ∞ to + ∞ ... goes from − ∞ to + ∞ " isn't sufficient. For example, consider x 2 = b ( e x − 1 − x 2 ) .
Hey bro, you forgot to add { } for b in last step in the floor function.
I used the same approach =).
We know that x − 1 is tangent to ln ( x ) . This is close to what we want, so let's work with it. Let's add 1 , getting that x is tangent to ln ( e x ) . That's closer - let's substitute x 2 for x , giving us that x 2 is tangent to ln ( e x 2 ) . Multiplying by e and substituting x / e for x gets us that x 2 is tangent to e ln ( x 2 ) , and simplifying gives us that x 2 is tangent to 2 e ln ( x ) .
Finally, log identities give us 2 e ln ( x ) = lo g e 1 / 2 e ( x ) .
Let's consider the difference function y = f ( x ) = x 2 − l o g b ( x ) = x 2 − l n ( b ) l n ( x )
We'll be studying this function on the domain: ( 0 , ∞ ] .
Let's study it derivative:
d x d y = 2 x − x ⋅ l n ( b ) 1
Let's find the extrema of f.
d x d y = 2 x − x ⋅ l n ( b ) 1 = 0
2 x = x ⋅ l n ( b ) 1
x = 2 l n ( b ) 1
Let's re-inject this to f.
y m = 2 l n ( b ) 1 − l n ( b ) l n ( 2 l n ( b ) 1 )
y m = 2 l n ( b ) 1 + l n ( 2 ) + l n ( l n ( b ) )
As x → 0 , y → ∞ . As x → ∞ , y → ∞ .
So we can see that if y m is positive, then y=0 has no solutions. If y m is negative, y=0 has two solutions.
y=0 has a single solution if y m = 0 .
y m = 0 ⇔ 1 + l n ( 2 ) + l n ( l n ( b ) ) = 0 ⇔ l n ( b ) = e − 1 − l n ( 2 ) = 2 e 1 ⇔ b = e 1 / 2 e
b = e 1 / 2 e = 1 . 2 0 1 9 4 3 3 6 8 4 . . .
⌊ 1 0 0 0 0 b ⌋ = 2 0 1 9
That point is the minima, not the maxima, of f . Apart from that, everything else follows.
Log in to reply
I meant to say an optima, since proving that it is a minima requires some further work.
Log in to reply
I've edited your solution to say "extrema".
"Optima" isn't a recognized word, though I guess you want "optimum".
x 2 = l n ( b ) l n ( x )
Consider the two curves, y = x 2 and y = l n ( b ) l n ( x ) = k l n ( x )
These two curves have exactly one solution implies that they have a common tangent i.e, both have same slope.
d x d y = 2 x = x k ⇒ k = 2 x 2
x 2 = 2 x 2 l n ( x ) ⇒ l n ( x ) = 2 1 ⇒ x = e 1 / 2
Now, ( e 1 / 2 ) 2 = k l n ( e 1 / 2 ) ⇒ k = ( 2 1 ) e = 2 e
Now, k = l n ( b ) 1 ⇒ l n ( b ) = k 1 = 2 e 1 ⇒ b = ( e ) 1 / 2 e = 1 . 2 0 1 9 4 3 3 6 8 4 7
⌊ 1 0 0 0 0 { b } ⌋ = ⌊ 1 0 0 0 0 × 0 . 2 0 1 9 4 3 3 6 8 4 7 ⌋ = ⌊ 2 0 1 9 . 4 3 3 6 8 4 7 ⌋ = 2 0 1 9
Henry ,maybe you should have posted this question on New Year Eve ,Year 2019!!
I know and it's only one month to wait, but I thought that there will be so many 2019 problems that you can simply guess them all, and I also don't have the patience to wait :D
Log in to reply
Yeah!! Its going to be FUN!!
Can you please let me know the Latex code for floordown function and fractional function.
Log in to reply
For floor it's
\lfloor ... \rfloor
It's important to put l and r for left and right before "floor" to make clear which direction the brackets should point.
The fractional function is (as far as I know) just the same as for sets
\{ ... \}
Why is it that "These two curves have exactly one solution implies that they have a common tangent"?
For example, the curves y = x and y = 2 x have exactly one solution, but have no common tangent. So, what other conditions are you missing / what assumptions are you making?
Log in to reply
I equated the derivatives, in your case the derivatives of your equations dont equate ( 1 = 2 ) , so they have no common tangent . It is based on the slope of both curves that I equated and they have one solution implies all you have to do is equate those slopes.
Henry U already specified that they touch only once, and we have to calculate that value of b , because for any other value , the graphs, y = x 2 and y = lo g b x have either two or no point of intersection .
Log in to reply
I understand that you equated the derivatives. The question is how do you know that they must have a common tangent? Or is that an assumption that you are making?
For example, if we tried to solve for when " x = b x has exactly one real solution", if we applied the logic of "they have a common tangent, so by taking derivatives 1 = b ", then that would give us an incorrect answer.
So, what other condition is inherent to these two curves that allow us to conclude "they have a common tangent"?
Note: The problem didn't specify "touch" (which some might say implies that there is a common tangent), but just "has exactly one real solution".
Log in to reply
@Calvin Lin – In your x = b x , both the curves are straight lines and straight lines are tangent of themselves and your solution of b = 1 holds true there. Consider a straight line a x + b y + c = 0 .Its slope is m = − b a .Let it pass through a point ( α , β )
Equation of its tangent will be, ( y − β ) = m ( x − α ) ⇒ b y + a x − ( a α + b β ) ⇒ a x + b y + c = 0 . You can vary ( α , β ) as far as they lie on the line and you always get c = a α + b β .
Infact any two curves can have a common tangent and all you have to do just find a straight line that touches both curves. Calculate the slope of that line which by definition equals the derivative of the curves at that point and find the tangent.
Log in to reply
@A Former Brilliant Member – The counterexample isn't restricted to "straight lines". Here's an example with curved lines: x 2 + x = x 2 + b x . For a more complicated example, consider x 2 = b ( e x − 1 − x 2 ) .
Note: I'm not disputing that "two curves can have a common tangent". I'm asking "why does f ( x ) = g ( x ) at exactly one point imply that f ′ ( x ∗ ) = g ′ ( x ∗ ) "? I have given several counterexamples, which means that this statement needs additional conditions in order to be true.
Log in to reply
@Calvin Lin – I think the condition for this step is that x 2 grows faster than lo g b x as x goes to infinity, but x 2 < lo g b x for some values of x (for example x = 1 .
Log in to reply
@Henry U – Not quite, as the inequality sign is incorrect. But otherwise, that's a good case.
I've added a solution to help discuss this in more detail since most people have this misconception.
A solution has x 2 = lo g b x = ( lo g b e ) ( ln x ) = ln b ln x so that ln b = x 2 ln x and b = e x 2 ln x .
Also, at the intersection point the derivatives have to be equal, because otherwise there will be two intersection points and solutions(*).
So 2 x = x lo g b e ⇒ 2 x 2 = lo g b e ⇒ ln b = 2 x 2 1 . Above we already saw that ln b = x 2 ln x so that we can solve x from x 2 ln x = 2 x 2 1 ⇒ ln x = 2 1 ⇒ x = e .
Now b = e e ln e = e 2 e 1 = 1 . 2 0 1 9 4 3 3 . . so that the requested answer is 2 0 1 9
A little bit early maybe, but Happy New year!
(*)This is because the second derivative of x 2 is 2 (positive), while the second derivative of lo g b ( x ) is − x 2 lo g b e (negative) on the entire (positive real) domain, as can also be seen from the graph. As x → ∞ the tangent of the red curve goes to + ∞ and that of the blue curve goes to 0; whereas when x → 0 + , the tangent of the red curve goes to 0 and that of the blue curve goes to − ∞ .
Used WolframAlpha to obtain almost a real solution by adjusting value of 'b':
solve x^2 = log(x)/log(1.2019435)
x = 1.64872 + 0.000899216i
x = 1.64872 - 0.000899216i
The b=1.2019435 as above was bracketed as follows:
The two curves are either (1) cutting at two places giving two real roots or (2) not touching each other giving complex roots.
Therefore, imaginary part vanishing shows that two curves are touching each other at x = 1.64872.
The following answer of complex roots was obtained at b=1.20199 :
x = 1.64852 - 0.0169286 i
x = 1.64852 + 0.0169286 i
The following answer of two real roots was obtained at b=1.2019 :
x = 1.63258
x = 1.66524
Answer=2019
We are only plotting the values of x on the (real) Cartesian plane. I don't see how solving for the complex roots of x will help here. Can you elaborate on it?
Log in to reply
The two curves are either (1) cutting at two places giving two real roots or (2) not touching each other giving complex roots.
Therefore, imaginary part vanishing shows that two curves are touching each other at x = 1.64872.
The following answer of complex roots was obtained at b=1.20199 :
x = 1.64852 - 0.0169286 i
x = 1.64852 + 0.0169286 i
The following answer of two real roots was obtained at b=1.2019 :
x = 1.63258
x = 1.66524
Try similar problems Common Point and Common Tangent .
Note: The first 2 solutions to Common Point commit the same error that I pointed out, namely assuming that we must have a common tangent.
Log in to reply
Thank you, Calvin. By the way, could you please tell me how to add some text to the bottom of the picture?
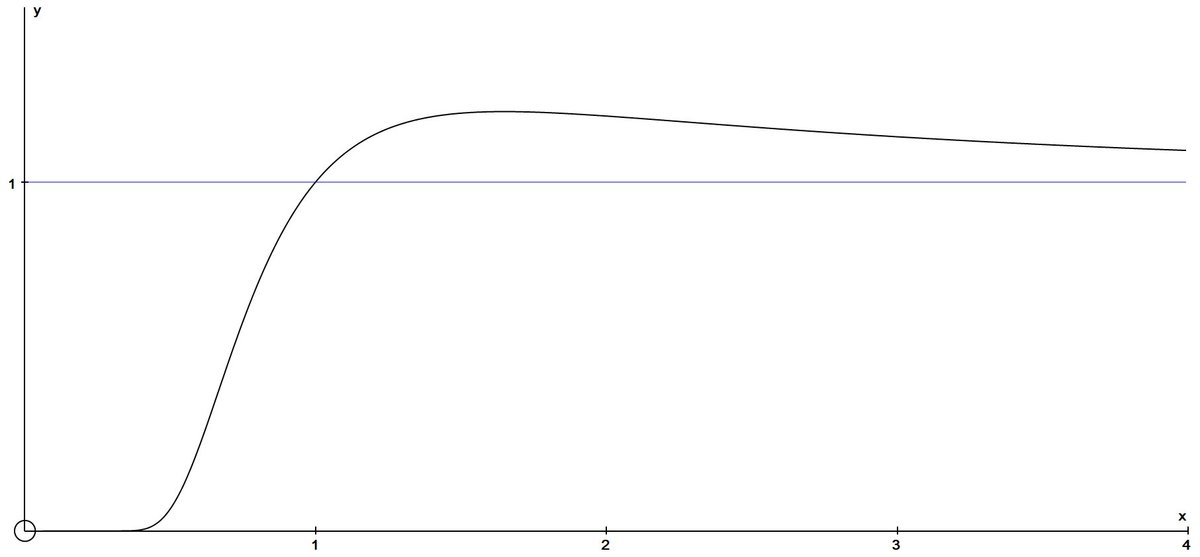
The curves only touch once.
Log in to reply
We use markdown syntax, which is

. So, to add some text to the bottom of the picture, replace the "title" in the syntax.
I've edited your comment to give you a reference. You can hit the edit button to see an explicit example.
x 2 = lo g b x = ln b ln x , 2x=\dfrac{1}{x\ln{b} .
x 2 ln b = ln x = 2 1 , x = e .
Thus, b = e 2 e 1 .
If you read the other solutions, you will notice that a lot of people made the assumption that:
Unfortunately, this claim need not be true. Lots of curves can intersect once, and not share a common tangent at the point of intersection. Can you find various counterexamples (of essentially different scenarios) where there isn't a common tangent?
Hint: Think about your favourite function h ( x ) where h ( x ) = 0 has a unique solution at x = x ∗ and h ′ ( x ∗ ) = 0 . Then, set f ( x ) = h ( x ) + g ( x ) .
Note: h ( x ) is ultimately the crux to analyze.
So, when must we have a common tangent? What additional assumption about these functions is being used? Can you list some in the comments?
More concretely, what are the conditions that when placed on a (differentiable) function h ( x ) : [ 0 , 1 ] → R that will allow us to conclude that h ′ ( x ∗ ) = 0 ? By setting h ( x ) = f ( x ) − g ( x ) , we reach our goal of determinining when the uniqueness of a solution implies a common tangent f ( x ) = g ( x ) , f ′ ( x ) = g ′ ( x ) .
Example 1 : If h ( x ) = 0 has a unique solution at x = x ∗ and h ( 0 ) h ( 1 ) > 0 , then h ′ ( x ∗ ) = 0 .
Proof: h ( 0 ) × h ( 1 ) > 0 means that they have the same sign. WLOG, suppose that h ( 0 ) , h ( 1 ) > 0 .
Proof by contradiction. Suppose h ′ ( x ∗ ) = 0 . WLOG, suppose that h ′ ( x ∗ ) < 0 .
Then, there exists an ϵ > 0 such that ϵ h ( x ∗ + ϵ ) − h ( x ∗ ) < 0 ⇒ h ( x ∗ + ϵ ) < 0 .
Then, by the intermediate value theorem, we can conclude that in the interval [ x ∗ + ϵ , 1 ] , there must be another solution to h ( x ) = 0 .
This contradicts that there is a unique solution in [ 0 , 1 ] .
Note: The condition of [ f ( 0 ) − g ( 0 ) ] × [ f ( 1 ) − g ( 1 ) ] > 0 is typically the one that people think of in such a scenario, but then have difficulty expressing it clearly.
Note: The condition doesn't need to apply to the endpoints of the function's domain. It just needs to apply to an interval containing the unique solution. Note: In case it wasn't obvious, the conditions are sufficient, but not necessary. IE Just because the function fails the conditions doesn't mean that we must have h ′ ( x ∗ ) = 0 .
Corollary: This applies to the given problem.
(Suggested by Henry) Example 2 : If h ( x ) = 0 has a unique solution at x = x ∗ and h ′ ( x ) > 0 on ( x ∗ , 1 ] , , then h ′ ( x ∗ ) = 0 .
This doesn't work. Can you come up with a counterexample? Can you tweak this condition so that it will work?
(Suggested by Antoine) Example 3 : If h ( x ) = 0 has a unique solution at x = x ∗ and h ′ ′ ( x ) > 0 , then h ′ ( x ∗ ) = 0 .
This doesn't work. Can you come up with a counterexample? Can you tweak this condition so that it will work?