Intersection points on circle, part 2
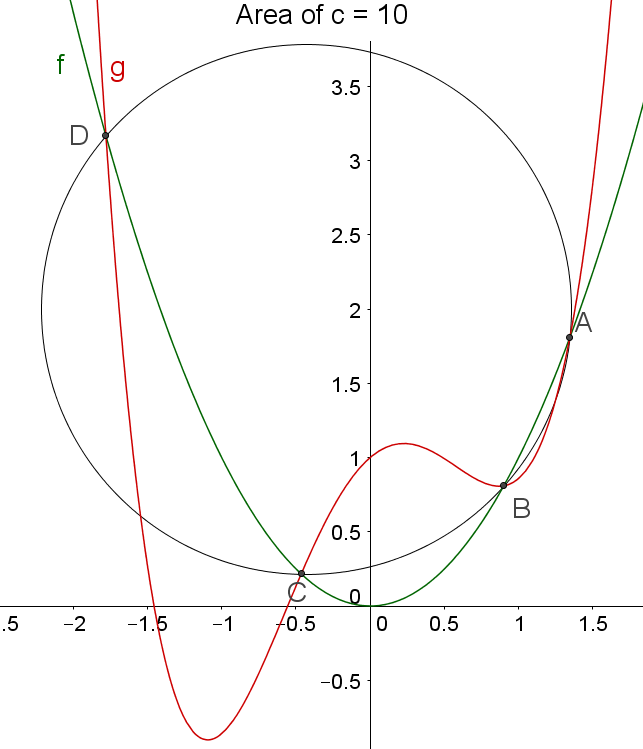 The parabola
f
(
x
)
=
x
2
intersects the graph of
g
(
x
)
=
x
4
+
a
x
3
−
2
x
2
+
b
x
+
1
at four distinct points. These four points on a same circle of area 10. Given that
b
>
0
, find the value of
⌊
1
0
0
0
b
⌋
.
The parabola
f
(
x
)
=
x
2
intersects the graph of
g
(
x
)
=
x
4
+
a
x
3
−
2
x
2
+
b
x
+
1
at four distinct points. These four points on a same circle of area 10. Given that
b
>
0
, find the value of
⌊
1
0
0
0
b
⌋
.
This problem is part of Curves... cut or touch?
The answer is 855.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
This is the solution that I had come up with however due to some silly mistakes in evaluating 2 2 as 1 6 I got some wacky answers. This is the most elegant way to solve this problem. +1.
The coefficient of x 2 in x 4 + a x 3 − 2 x 2 + b x + 1 is − 2 , so 2 q − 1 = 2 .
Log in to reply
We are comparing with coefficients in f − g , not g .
Log in to reply
You're right, my mistake. :P
Could you explain why does that comparing with f-g work?
Suppose the equation of the circle is ( x − h ) 2 + ( y − k ) 2 = r 2 .
Since the circle's area is 10 and it intersects with the graph f ( x ) = x 2 , the above equation can be rewritten as ( x − h ) 2 + ( x 2 − k ) 2 = π 1 0 . Expand it and we get x 4 − ( 2 q − 1 ) x 2 − 2 p x + ( p 2 + q 2 − π 1 0 ) = 0
Compare the above equation with g ( x ) − f ( x ) , we obtain
2 q − 1 − 2 p p 2 + q 2 − π 1 0 = = = 3 b 1
From the first equation, q = 2 ; from the last equation, p = ± π 1 0 − 3 ; finally from the second equation, b = 2 π 1 0 − 3 ≈ 0 . 8 5 5 8 0 1 (as b > 0 ) . So ⌊ 1 0 0 0 b ⌋ = 8 5 5 .