Intriguing Ornament (the End)
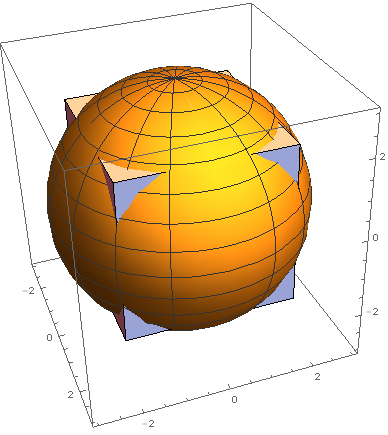
At the home of a comrade I noticed an unusual holiday ornament the other day that consists of a sphere and a concentric cube. It would have been inappropriate to take a picture under the circumstances, but, fortunately, I found a somewhat similar picture online (the picture is a bit misleading, though). I was able to determine that the cube has a side length of 4 centimeters and the diameter of the sphere is 6 cm. My comrade wants to apply a new coat of fancy paint to the spherical portion of the ornament, and he needs to know its surface area (in square centimeters). Can you help? (Round your answer to the nearest integer.)

The answer is 108.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Yes, that works too! Thank you for sharing! I'm using the "Hat-Box Theorem" too, of course; it goes in into the formula for the spherical cap.
I usually look for solutions that require a minimum of visualization. For one thing, I'm not very good at it, and, more importantly, I try to generalize to higher dimensions.
Log in to reply
I'm a very visual person. I was holding out for a geometrical solution until the very end. I managed to avoid a double integral, at least.
It's just that your picture is misleading. My first attempt at solving was to naively use R = 3 , a = 4 from your first problem, which gives the erroneous 3 6 π but doesn't take into account the fact the spherical caps overlap each other. I think it's just a coincidence, but this is the same as the area of the whole sphere! This implies the overlap from that formula is equal to the portion hidden by the cube. Although this is interesting, I couldn't figure out how to use this information, as that area is equally hard to find.
Log in to reply
I did warn people in the problem that the figure is misleading... I think it's part of the problem's "intrigue." ;)
As you can see, I was approaching this in a set theoretical, inclusion-exclusion kind of way, computing the volumina of the caps where one variable has an absolute value exceeding 4, and then subtracting the overlaps, where we have two "large" variables. This way, I can avoid any need for visualization.
The fact that the sum of the areas of the caps is 3 6 π , the surface area of the sphere, is no coincidence, of course: It's a consequence of the height of each cap being a sixth of the diameter (again: the Hat-Box Theorem at work).
As much as I am a fan of brute-force methods, I look forward to seeing more elegant solutions to this one...
We have to first be aware that the given figure does not accurately depict the object described in the problem. Since a = 4 and R = 3 , most of the exposed area is the sphere's. Therefore, a reasonable approach would be to subtract the sphere's unexposed areas from 4 π R 2 = 3 6 π . By symmetry, the unexposed area is 8 times the area of the sphere that is eclipsed by the cube (see figure). So A unexposed = 8 ∬ eclipsed R 2 sin θ d θ d ϕ .
Most of the work lies in figuring out the bounds for θ and ϕ . From the "side view," it is not so difficult to get arccos ( 3 2 ) ≤ θ ≤ arccos ( 3 1 ) . From "top view," we find that how much ϕ is swept depends on θ as: 0 ≤ ϕ ≤ 2 π − 2 arccos ( 3 sin θ 2 ) . (*)
So, A exposed = 3 6 π − A unexposed = 3 6 π − 8 ∫ arccos ( 3 2 ) arccos ( 3 1 ) ∫ 0 2 π − 2 arccos ( 3 sin θ 2 ) 3 2 sin θ d ϕ d θ ≈ 1 0 7 . 6 3 2 ≈ 1 0 8 .
(*) At this step it's probably most helpful to make a sketch and see that ϕ is just 2 π minus the "other two angles," which are the same and equal to arccos ( 3 sin θ 2 ) .
Very nicely done, Comrade! The figure goes a long way in explaining what is going on.
Log in to reply
Thanks, Otto. I have an idea for a follow-up problem, inspired by this one: "Find the sum of the angles of a spherical triangle defined by an intersection of the cube and the sphere." I think once one knows how to solve the original problem (yours), finding the answer to this question (mine) is just a simple, yet worth knowing, extra step.
Log in to reply
Yes, that is a great idea, Comrade! Do you mean the solid angle?
Log in to reply
@Otto Bretscher – Oh, no. What I mean is the sum of the angles of the ``spherical triangle'' form by the intersection of the cube and the sphere.
Log in to reply
@Huan Bui – Oh well, I posted a rather silly problem on solid angles anyway; I think it is good for people to learn about those.
It may be worth mentioning that the surface area of the "eclipsed" portion in the first octant (where x , y , z ≤ 2 ) can also be found in Cartesian coordinates: ∫ 1 2 ∫ 5 − x 2 2 9 − x 2 − y 2 3 d y d x ≈ 0 . 6 8 3 2 . We can find the limits of integration in a purely algebraic way, without any need for geometrical insight.
I hope you will repost your spherical triangle problem. I saw it got deleted just as I was about to answer it
Log in to reply
I have to think about it a little bit more - the problem turns out to be more complicated than I thought... I just realized I made a precarious assumption.
Comrade Huan has written a very careful solution, using spherical coordinates. For the sake of variety, let me propose a solution based on Cartesian coordinates; I find it easier to figure out the limits of integration that way (but this is a matter of taste and habit).
We can start by observing that each of the six caps (where the absolute value of one of the variables is ≥ 2 ) has a surface area of S c a p = 2 π R h = 6 π . But we cannot simply add those surface areas up since, along each of the 12 edges, the two adjacent caps will intersect in a "lune," as Huan's figure illustrates. Focusing on the lune y ≥ 2 and z ≥ 2 , the intersection of the caps z ≥ 2 and y ≥ 2 , we find S l u n e = ∫ − 1 1 ∫ 2 5 − x 2 9 − x 2 − y 2 3 d y d x ≈ 0 . 4 5 5 4 7 7 . The surface area we seek is 6 S c a p − 1 2 S l u n e = 6 0 π − 2 6 4 arctan ( 2 ) + 7 2 arctan ( 2 1 1 ) + 2 4 0 arctan ( 2 1 ) ≈ 1 0 7 . 6 3 ≈ 1 0 8 . (This is a primitive case of the principle of inclusion-exclusion.)
I don't understand. You first approximated S lune to be 0.455477, I presume you used some computer assistance. Later, you are able to find the exact value of 6 ⋅ S cap − 1 2 ⋅ S lune . How is that possible?
Unless you have already found the exact value of S lune ? This looks like a daunting task, as WolframAlpha says that its exact value is 3 ( π + tan − 1 ( 1 1 7 5 3 1 0 2 9 6 ) − 8 cot − 1 ( 2 ) ) .
Were you able to solve this iterated integral with ease? I tried changing the order of the integration, but this doesn't look like it's easier to solve.
And where did the " y ≥ 2 , z ≥ 2 " part come from? Care to elaborate?
Log in to reply
I know that my comments are sometimes a bit (too) terse, Comrade; I'm sorry for that. My only excuse is that I'm a slow and bad typist. (In response to your inquiry, I have added a few much-needed comments to my solution.)
I found the closed form for S l u n e too, but I wrote it down for the final expression only. If you check the algebra (and trigonometry), you will see that our two expressions agree. If I had unlimited time, I could do it by hand, starting with ∫ 9 − x 2 − y 2 3 d x = 3 arctan ( 9 − x 2 − y 2 x ) , but the integral with respect to y would be exceedingly tedious to do (but possible in closed form); I cannot think of an altogether "effortless" way to do it.
Changing the order of integration is not going to help, since the given geometrical problem is symmetric in x , y , z .
"And where did the y ≥ 2 , z ≥ 2 part come from?" We are intersection the caps z ≥ 2 and y ≥ 2 , which gives the "lune" y ≥ 2 , z ≥ 2 (a primitive case of "inclusion-exclusion"). Luckily, all triple-wise intersections of caps are empty, so that we don't have to push the principle very far; subtracting the 12 lunes will suffice.
Log in to reply
Can you show some hints on how you tackle S lune (to find its exact value)? Like what substitutions you used? Or did you integrate by part? Did you use differentiation through the integral sign? ETC?
I still don't get the last paragraph. I'll have to come back to it when I have a clear mind.
Log in to reply
@Pi Han Goh – Update: Yeah nevermind, I got it. Change of order of integration gives S lune = 2 ∫ 2 5 ∫ 0 5 − y 2 9 − x 2 − y 2 3 d x d y . You have already solved for the inner integral. By parts with u to be the given integrand, and d v = d y , and followed by a substitution of w = y 2 , then Euler substitution.
Gawd, this is a handful.
Log in to reply
@Pi Han Goh – Great! Now what about this cap and lune business? So we have the six "caps," where one variable is more than 4 in absolute value, for example, z ≥ 4 and, separately, y ≥ 4 . They will intersect in a region where both inequalities hold simultaneously, z ≥ 4 and y ≥ 4 . Because of its shape it is suggestive to call this intersection a "lune" (look at Huan's figure). The rest is inclusion-exclusion.
Here's a better picture, showing the sphere is actually larger than shown.
(In fact, Otto, if you want to use this picture instead, you may. I could tone down the colors if you'd like.)
I found the surface area by projecting the sphere out to a cylinder and using Archimedes' Hat-Box Theorem
Let x be the height along the axis of the cylinder. With x = 0 the center, x = − 3 the bottom, and x = 3 the top. The regions where the sphere is pierced by the cube correspond to the intervals [ − 2 , − 1 ] and [ 1 , 2 ]
Let's look at cross sections in these intervals
On the left is a side view of the ornament with the vertical axis the axis of the cylinder. The dashed line is a cross section at height x and to the right is this top view of this section. The radius of this section is 9 − x 2 and the angle drawn is arccos 9 − x 2 2 .
The portion of a circle is 8 of these angles and the radius of the cylinder is 3, so the arc length at height x is given by 2 4 ⋅ arccos 9 − x 2 2 .
∫ 1 2 2 4 ⋅ arccos 9 − x 2 2 ≈ 1 6 . 1 1 7
The unobstructed portions of the sphere are 4 units along the axis so have area 4 ⋅ 6 π = 2 4 π
The total area is then 2 ⋅ 1 6 . 1 1 7 + 2 4 π = 1 0 7 . 6 3 2 so the final answer is 1 0 8 c m 2