Intro to Differential Equations - 2

Classical Mechanics Level 3

This time we will deal with differential equations of two variables. 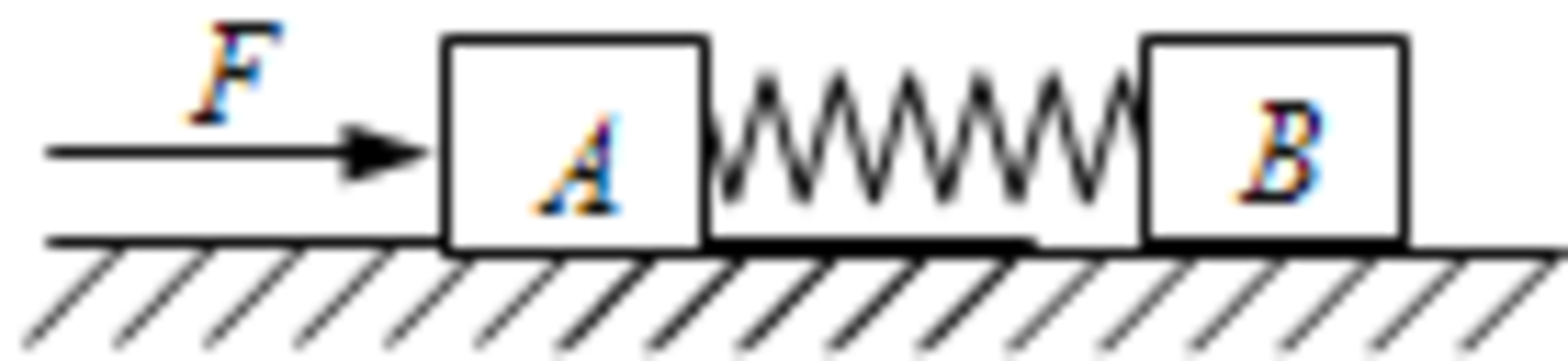As shown above, two blocks $A,B$ with the same mass $m$ are connected by a light spring with no damping satisfying the Hooke's law, whose spring constant is $k$ . Initially, they rest on the horizontal ground, and the spring is of its equilibrium length. Assuming the spring is long enough so that when it is compressed, the two blocks have no collision.

Now if we apply a force $F$ to block $A$ to the right horizontally, what is true when the spring is compressed most ?

Only if you find the answer will you truly understand what's really going on here.

Ignore all the frictions and air resistance.

0<a_{B}<\dfrac{F}{m}

a_{B}>\dfrac{F}{m}

It depends on the spring constant

k

a_{B}=0

a_{A}=\dfrac{F}{m}

0<a_{A}<\dfrac{F}{m}

a_{B}=\dfrac{F}{m}

1 solution

Steven Chase
Jul 24, 2019

Let $L$ be the length of the spring, and let $L_0$ be the un-stretched length.

$F + k(L - L_0) = m \ddot{x}_A \\ -k(L - L_0) = m \ddot{x}_B \\ x_B - x_A = L$

Subtracting the first equation from the second yields:

$-F + -2k(L - L_0) = m \ddot{L} \\ -2kL - F + 2k L_0 = m \ddot{L}$

Homogeneous equation:

$-2kL = m \ddot{L} \\ \ddot{L} = -\frac{2 k}{m} L$

This corresponds to simple harmonic motion of the following form (this is the homogeneous solution plus the particular solution):

$L = A cos(\omega t) + B sin(\omega t) + C \\ \omega = \sqrt{\frac{2k}{m}}$

Take some derivatives:

$L = A cos(\omega t) + B sin(\omega t) + C \\ \dot{L} = -A \omega \, sin(\omega t) + B \omega \, cos(\omega t) \\ \ddot{L} = -A \omega^2 \, cos(\omega t) - B \omega^2 \, sin(\omega t)$

Apply initial conditions for $L$ , $\dot{L}$ , and $\ddot{L}$ at $t = 0$ :

$L_0 = A + C \\ 0 = B \omega \implies B = 0 \\ -\frac{F}{m} = -A \omega^2 = - A \frac{2k}{m} \implies A = \frac{F}{2k} \\ C = L_0 - \frac{F}{2k}$

Plugging back in:

$L = \frac{F}{2k} cos(\omega t) + L_0 - \frac{F}{2k}$

The minimum length occurs when the cosine term is negative one:

$L_{min} = L_0 - \frac{F}{k}$

Evaluate the Newton's Second Law equations at this point:

$F + k(L_{min} - L_0) = m \ddot{x}_A \\ -k(L_{min} - L_0) = m \ddot{x}_B$

Plugging in:

$F + k(L_0 - \frac{F}{k} - L_0) = 0 = m \ddot{x}_A \\ -k(L_0 - \frac{F}{k} - L_0) = F = m \ddot{x}_B$

Results at max compression:

$\ddot{x}_A = 0 \\ \ddot{x}_B = \frac{F}{m}$

Here is a plot with some sample numbers (generated using numerical integration as a double-check on the hand analysis):

Good simluation. Can you show that it is always true regardless of what k is?

Alice Smith - 1 year, 10 months ago

Sure, I'll write up the formal derivation

Steven Chase - 1 year, 10 months ago

Formal derivation is up now

Steven Chase - 1 year, 10 months ago

Ok. I really appreciate it.

Alice Smith - 1 year, 10 months ago

@Alice Smith – @Steven Chase Sir is it possible to show how the blocks will show their motion after given a force F ,in the original image given by problem poster . ( As naturally( in real life) it seems like just the spring will max compress and then both (blocks) go together with some accleration forever. Otherwise can u explain how it(spring) will again expand as after compression in real life ) ?

Kudo Shinichi - 1 year, 10 months ago

@Kudo Shinichi – Both blocks will continue to move rightward on average, but the distance between them will vary sinusoidally.

Steven Chase - 1 year, 10 months ago

@Steven Chase – Got it Thx @Steven Chase Sir .

Kudo Shinichi - 1 year, 10 months ago

Intro to Differential Equations - 2

1 solution

0 pending reports