Introductory Olympiad Algebra - The Square Is Now Complete
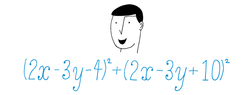 As
(
x
,
y
)
ranges over all pairs of real values, what is the smallest value of
As
(
x
,
y
)
ranges over all pairs of real values, what is the smallest value of
( 2 x − 3 y − 4 ) 2 + ( 2 x − 3 y + 1 0 ) 2 ?
The answer is 98.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
You could also tackle this through Cauchy-Schwarz: once again set z = 2 x − 3 y , and note that 2 [ ( z − 4 ) 2 + ( z + 1 0 ) 2 ] = 2 [ ( 4 − z ) 2 + ( z + 1 0 ) 2 ] ≥ [ 4 − z + z + 1 0 ] 2 = 1 9 6 , implying that ( z − 4 ) 2 + ( z + 1 0 ) 2 ≥ 9 8 .
Log in to reply
Of course, there are many methods of proving that the minimum is 98.
Do you know how to use AM-GM on this question? You have to be careful with the application, since AM-GM (mostly) applies only to non-negative values.
Log in to reply
Let z = 2 x − 3 y as it was.
1 4 = ( 4 − z ) + ( z + 1 0 ) ≥ 2 ( 4 − z ) ( z + 1 0 )
( 4 − z ) ( z + 1 0 ) ≤ 4 9
1 9 6 = ( ( 4 − z ) + ( z + 1 0 ) ) 2 = ( 4 − z ) 2 + 2 ( 4 − z ) ( z + 1 0 ) + ( z + 1 0 ) 2
( 4 − z ) 2 + ( z + 1 0 ) 2 = 1 9 6 − 2 ( 4 − z ) ( z + 1 0 ) ≥ 1 9 6 − 2 ( 4 9 ) = 9 8 ~~~
without using any results , differentiation or parabola properties : convert ( z − 4 ) 2 + ( z + 1 0 ) 2 to ( a − k ) 2 + ( a + k ) 2 where a is variable and k is constant and which is equal to 2 a 2 + 2 k 2 and thus minimum value would be at a=0
the given eq can be written as ( a − 7 ) 2 + ( a + 7 ) 2 where a = z+3 thus minimum value is 2 ∗ 7 2 = 9 8
Log in to reply
I also calculate this question like you did here but do not know what theories support my calculation. Please help explain more about "differentiation or parabola properties". Thank you in advance.
Exactly. I solved in an identical way by realizing that you could set 2 x − 3 y equal to some variable. Why is this not letting me say just "Exactly"? It's giving me a message saying "Please provide a more complete explanation of your question or response before submitting a reply. Thanks!". :O
Log in to reply
To avoid comments/solutions where people simply post the answer, we've added a minimum limit of 10 characters.
Log in to reply
WHAT? That means no more of my beautiful, one sentence solutions... *tear. ;|
"The answer is blablabla ." takes more than 15 characters. =__="
I thought it would also be important to note that 2x-3y is a straight (non horizontal) line meaning it has an all encompassing range and thus we know that z can be any value. Had z been a more complex function with an incomplete range, this may not have worked out right?
Guuhhhh! i got the -3 and substituted it back in the quadratic and ended up with 116!! T.T
thanks man. absolutely correct
( 2 x − 3 y − 4 ) 2 + ( 2 x − 3 y + 1 0 ) 2 = ( 2 x − 3 y + 1 0 − 1 4 ) 2 + ( 2 x − 3 y + 1 0 ) 2 = ( 2 x − 3 y + 1 0 − 1 4 ) ( 2 x − 3 y + 1 0 − 1 4 ) + ( 2 x − 3 y + 1 0 ) 2 = ( 2 x − 3 y + 1 0 ) ( 2 x − 3 y + 1 0 − 1 4 ) − 1 4 ( 2 x − 3 y + 1 0 ) + 1 4 2 + ( 2 x − 3 y + 1 0 ) 2 = ( 2 x − 3 y + 1 0 ) ( 2 x − 3 y + 1 0 ) − 2 8 ( 2 x − 3 y + 1 0 ) + 1 4 2 + ( 2 x − 3 y + 1 0 ) 2 = 2 ( 2 x − 3 y + 1 0 ) 2 − 2 8 ( 2 x − 3 y + 1 0 ) + 1 9 6 l e t A = 2 x − 3 y + 1 0 f ( A ) = 2 A 2 − 2 8 A + 1 9 6 d A d f ( A ) = 4 A − 2 8 = 0 A = 7 f ( 7 ) = 2 ( 7 ) 2 − 2 8 ( 7 ) + 1 9 6 = 9 8
USING STRAIGHT LINE CONCEPT : see the two equations as the equations of straight lines and then any point lying on the perpendicular joining them would have min. distance (since both given lines are parallel) and then randomly take any line perpendicular to both of them and then using the relation btw x and y using that equation substitute in the given relation .........in question after then apply max min concept
Interesting solution 🤔
take 2x-3y=k and replace it inthe exp,now maxima minima
let z=2x-3y and solve it using maxima and minima techinque or using properties of parabola
Set z = 2 x − 3 y + 3 , we want to find the minimum of ( z − 7 ) 2 + ( z + 7 ) 2 = 2 ( z 2 + 4 9 )
The minimum occurs at 2 x 49 = 98 when z 2 = ( 2 x − 3 y + 3 ) 2 = 0
Let p = 2 x − 3 y and let the whole expression be equal to y Then,
( p − 4 ) 2 + ( p + 1 0 ) 2 = y
p 2 − 8 p + 1 6 + p 2 + 2 0 p + 1 0 0 = y
2 p 2 + 1 2 p + 1 1 6 = y
2 ( p 2 + 6 p + 5 8 ) = y
2 ( p 2 + 6 p ) = y − 1 1 6
2 ( p 2 + 6 p + 9 ) = y − 9 8
2 ( p + 3 ) 2 + 9 8 = y
We could make ( p + 3 ) 2 = 0
Then y = 0 + 9 8
y = 9 8
Therefore, the minimum value of the expression ( 2 x − 3 y − 4 ) 2 + ( 2 x − 3 y + 1 0 ) 2 is 9 8
Let z= 2x -3y Substituting z in the given equation we get (z-4)^2 +(z+10)^2 → 2z^2 +12z + 116→ 2(z^2 +6z +9) + 98→ 2(z+3)^2 + 98
The minimum value is obtained when z = -3 so that the square part become zero as it cannot be negative for real value of z So min value is 98...
Set 2x-3y = n, so: (n-4)^2 + (n+10)^2 = 2n^2+12n+116. Because the a-coefficent is positive, so the minimum occurs at the vertex, which is n = (-b)/2a = (-12)/4 = -3. Plug this into the quadratic equation above, we get the value of 98. So the minimum of (2x-3y-4)^2 +(2x-3y+10)^2 is 98.
My solution is kinda weird. I'll just post it up for comments.
So first I started out getting the expanded form of the expression.
8 x 2 + 2 4 x − 2 4 x y − 3 6 y + 1 8 y 2 + 1 1 6
Next, I formed two quadratic expressions
[ 1 ] : 8 ( x + 2 3 ) 2 − 1 8
[ 2 ] : 1 8 ( y − 1 ) 2 − 1 8
Leaving out a remaining [ 3 ] : − 2 4 x y + 8 0 .
Then I got the minimum values of [ 1 ] and [ 2 ] , which are at x = − 2 3 and y = 1 , respectively.
But [ 3 ] would give a high positive value if x and y have different signs so I let x = 0 and with a help of a calculator I got an answer of 9 8 .
Just found out, too, that the same happens if I let y = 0 .
Any comment would help, since it got me to the right answer I thought this approach has any use in itself. If it has not, then this technique goes to the trash bin.
You need to clearly explain when the minimum occurs. For example, if x , y > 0 then − 2 4 x y could be really negative, thereby reducing the value even further. So, how do you know that you've not found the actual minimum.
Hi, I had a similar solution. 2 (2x+3)^2 + 2 (3y-3)^2 - 24xy + 80 Same results for x and y. If we use 0 for x or y, the missing 18 shows up as result of the first or second term! But weird, like before. :-)
Log in to reply
The reason for that observation is that the minimum occurs when 2 x − 3 y = − 3 .
2x-3y=k --> (k-4)²+(k+10)²=2k²+12k²+18-18+116=2(k+3)²+98. setting 2x-3y=-3 --> min=98
Since 2x-3y can take any value, the answer is half the difference (-4 - (-10)) = -7, squared (49), then doubled as the two halves are summed, hence 98.
Define the function $f\colon \mathbb{R}^2 \to \mathbb{R}\colon (x,y) \mapsto 2x-3y+3$. Each section of this map of suriective, and in particular also the function itself. Hence the expression can be rewritten as $(X+7)^2+(X-7)^2$, where $X=f(x,y)$ can be any real value. At this point, it is enough to expand :)
Set z = 2 x − 3 y , we want to find the minimum of ( z − 4 ) 2 + ( z + 1 0 ) 2 = 2 z 2 + 1 2 z + 1 1 6 . The minimum occurs at the vertex of the parabola, which is z = − 2 × 2 1 2 = − 3 . Hence the minimum is ( − 3 − 4 ) 2 + ( − 3 + 1 0 ) 2 = 9 8 .