Inverse Collatz Problem

I generate the list backward : thus, if for a given number $n$ it takes $p$ steps to reach 1 for the first time, then

• it takes $p + 1$ steps for the number $2n$ ;

• it takes $p + 1$ steps for the number $\tfrac13(n-1)$ , provided this is an odd integer. This happens when $n$ has remainder 4 after division by six. Also, we exclude the case $n = 4$ , because that would simply give us back the number 1.

I decided to use old-fashioned C. The data structure is a simple queue: new numbers are written at position write ; they are read at position read . At any given point, the number of items "on hold" is equal to write - read . As soon as we exhaust the numbers that took 15 steps, we know that the remaining values in the queue are all that take 16 steps.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

#include<stdio.h>

int main() {
    struct {
        int value;
        int steps;
    } queue[10000];

    int write = 0, read = 0, v;

    queue[write].value = 1;
    queue[write].steps = 0;
    write++;

    while (write > read && queue[read].steps < 16) {
        v = queue[read].value;

        if (v % 6 == 4 && v > 4) {
            queue[write].value = (v - 1)/3;
            queue[write].steps = queue[read].steps+1;
            write++;
        }

        queue[write].value = 2*v;
        queue[write].steps = queue[read].steps+1;
        write++;

        read++;
    }

    printf("%d values: \n", write - read);
    while (read < write)
        printf("%d  ", queue[read++].value);
}

Output:

1
2
3
4
5
6

29 values: 

1536  7  44  45  272  276  277  1664  46  280  282 
1696  1704  1706  10240  10752  300  301  1808  
1812  1813  10880  302  1816  1818  10912  10920  
10922  65536  

The largest possible value to reach $1$ in $16$ steps is $2^{16} = 65536$ , so we do not need to check higher. $65536$ will keep halving a total of $16$ times until it reaches $1$ , and any larger value will need to halve at least $17$ times.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

int[] prevInfo = {0, 0};
int index = 1;

while(index <= 65536){

    int numMoves = 0;
    int currTest = index;

    while(currTest != 1){

        if(currTest%2 == 0)
            currTest /= 2;
        else
            currTest = currTest * 3 + 1;

        if(currTest < index){

            numMoves += prevInfo[currTest];
            currTest = 1;

        }

        numMoves++;

    }

    int[] temp = new int[prevInfo.length+1];

    for(int i = 0; i < prevInfo.length; i++)
        temp[i] = prevInfo[i];

    temp[index] = numMoves;
    prevInfo = temp;


    if(numMoves == 16)
        System.out.print(index+", ");

    index++;

}

The $29$ integers are $7, 44, 45, 46, 272, 276, 277, 280, 282, 300, 301, 302, 1536, 1664, 1696, 1704, 1706, 1808, 1812, 1813, 1816, 1818, 10240, 10752, 10880, 10912, 10920, 10922,$ and $65536$ .

I tried to generate the list backwards using recursive function with this rule.

• if $\frac{n-1}{3}$ is an odd postive integer except 1 then the previous n is $2n$ or $\frac{n-1}{3}$ , if not then the previous n is only $2n$

With this, I generate a function as shown below

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

#include <iostream>

using namespace std;
int collatzbackwards(long long n, int m) { // m to count the steps
    if (m == 16) {
        cout << n << endl; // to print the numbers
        return 1;
    }
    else if ((n - 1) / 3 != 1 && (n - 1) % 3 == 0 && ((n - 1) / 3) % 2 == 1)
        return collatzbackwards((n - 1) / 3, m + 1) + collatzbackwards(n * 2, m + 1);
    else
        return collatzbackwards(n * 2, m + 1);
}
///////////////////////////////////////////
int main(){

    cout <<"Total : "<< collatzbackwards(1, 0);
    return 0;
} 

Simple Python Solution:

    collatzNumbers = [[1]]

    def backCollatz():
      l = []
      for n in collatzNumbers[-1]:
        l.append(n*2)
        g = ((n-1)/3.0)
        if g % 2 == 1 and not g == 1:
          l.append(int(g))
      collatzNumbers.append(l)
      # print a

    for i in range(16):
      backCollatz()

    print len(collatzNumbers[-1])

A simple approach is the recursive approach. Considering all the integers as nodes in a graph and pointing an integer to the next integer by the Collatz rule, we get a directed acyclic graph. We backtrack along this graph to find the number of nodes that are a "Collatz distance" of 16 from the node 1.

• Problem : Count the number of nodes (integers) that are a "Collatz distance" of $r$ from the node (integer) $n$
• Solution : Count the number of nodes (integers) that are a "Collatz distance" of $r-1$ from the one or two parent nodes of the node (integer) $n$

We note that, by the Collatz rule, we can always get $n$ from $2n$ since $2n$ is always even. We can also get $n$ from $\frac{n-1}{3}$ if said number is an integer and is even, which happens only when $n \equiv 4 \, (\text{mod } 6)$ . We do not consider this rule when $n = 4$ since it loops back to 1.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

# Counts the number of integers that take r Collatz sequence steps to reach the number n
def collatzDistance(r, n=1):
    if r == 0:
        return 1
    else:
        if n > 4 and n % 6 == 4:
            return collatzDistance(r-1,2*n) + collatzDistance(r-1,(n-1)//3)
        else:
            return collatzDistance(r-1,2*n)

print(collatzRadius(16))

The program terminates quickly with the answer 29 .

I used java:

 public static void main(String[] args) {
    ArrayList<Integer> a = new ArrayList<Integer>();

    for(int i = 5; i <= Math.pow(2,  16); i++) {
        if(collatz(i, 0) == 16) {
            a.add(i);
        }
    }
    System.out.println(a.toString());
    System.out.println(a.size());
}

public static int collatz(int num, int steps) {
    if(num == 1) {
        return steps;
    } else if (steps > 16) {
        return 0;
    } else if (num % 2 == 1) {
        return collatz(3*num + 1, steps + 1);
    } else {
        return collatz(num / 2, steps + 1);
    }
}

My solution is in python. I know that the biggest number that requires 16 steps is 2^16 = 65536, all the numbers bigger than 65536 will need more than 16 steps, so my program tries all the numbers from 7 to 65536. When the number is odd, I do two steps in one, because after have multiplied by 3 and added 1, the number is even, and the next step is always to divide by 2.

All the numbers (except 4, 2 and 1 obviously) finish their series with 16, 8, 4, 2, 1. It's because there is no integer n, such that n * 3 + 1 = 8, and the only solution for n * 3 + 1 = 4 is 1. Therefore, the programm stops at 8 and not at 1, to save some time, and the number of steps must be 13. The programm does not stop when the number equals 16, because if the number arrives at 5, it would directly reach 8 and skip the verification.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

solutions = []
for number in range(7, 65537) :
    iterations = 0
    curr_number = number

    while curr_number != 8 and iterations < 14:

        if curr_number % 2 :
            curr_number = (curr_number * 3 + 1) / 2
            iterations += 2

        else :
            curr_number = curr_number / 2
            iterations += 1

    if iterations == 13 :
        solutions.append(number)

print(solutions)
print("There are ", len(solutions), " solutions.")

Here's my code using Dev C++

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

#include<stdio.h>
unsigned int n1=1,n2,step=1,exitv=0,total=0;
int main()
{
    while(exitv==0)
    {
    step=0;
    n2=n1;
        do
        {
        if(n2%2==0)
        n2=n2/2;
        else
        n2=3*n2+1;

        step=step+1;
        }while(n2!=1);
    if(step==16)
    {
        total=total+1;
        printf("[%d]  %d goes to 1 within 16 steps \n",total,n1);
    }
    n1=n1+1;
    if(n1>65536)
        exitv=0;
    }
}

After running the program, it should look like this:

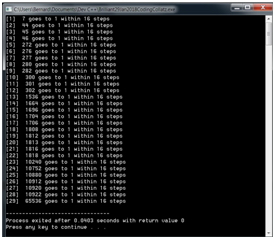
(The reason why $65536$ is the highest number to test for is because it will either divides $2$ or multiplies by $3$ then add $1$ so clearly, if it's something bigger than $65536$ , it will eventually hit odd numbers and get multiplied by $3$ unless if it's a power of $2$ .)

Running the code, there should be $29$ numbers as listed, hence the answer is $\boxed{29}$ .

2^16=65536 is the largest value which would take 16 steps. Any larger number would take more steps.

If a number already took more than 16 steps then it slips out of the nested for loop. If a number reaches 1, also slips out of the nested for loop. And each time a number slips start_num increases by 1...

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

#inlcude <stdio.h>

int main() {
    int start_num, a, b, i, count=0;
    for(start_num=1; start_num<=65536; start_num++) {
        a=start_num;
        for(i=0; i<=16; ) {
            if(a%2==0) {
                b=a/2;
                i++;
                a=b;
                if(a==1) {
                    break;
                }
            }
            else if(a%2!=0){
                b=(a * 3) +1;
                i++;
                a=b;
            }
        }
        if(i==16) {
            count++;
            printf("%d ,", start_num);
        }
    }
    printf("\nThey all take 16 steps. \n\n%d numbers in total....\n", count);
}

Output :

1
2
3
4

7, 44, 45, 46, 272, 276, 277, 280, 282, 300, 301, 302, 1536, 1664, 1696, 1704, 1706, 1808, 1812, 1813, 1816, 1818, 10240, 10752, 10880, 10912, 10920, 10922, 65536,
They all take 16 steps.

29 numbers in total....

Python straightforward solution:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

steps_16 = 0
for num in range(1,2**16+1):
    loc_steps = 0
    loc_num = num
    while (loc_num != 1):
        loc_num = loc_num / 2 if loc_num % 2 == 0 else loc_num * 3 + 1
        loc_steps += 1
    if (loc_steps == 16):
        steps_16 += 1
print steps_16 

Please someone tell me how to defeat this strange formatting system, cause I fail for some reason...

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

C = {} ; % Cell array to save on index k each number n taking k steps to reach one 
for n = 2:2^16
    N = n ;
    k = 0 ;
    while N > 1
        switch mod(N,2)
            case 1
                N = 3*N + 1 ;
            case 0
                N = N / 2 ;
        end
        k = k + 1 ;
    end
    if size(C,2) < k
        C{k} = n ;
    else
        C{k} = [C{k}, n] ;
    end
end
size(C{16},2) % Numbers taking 16 steps

$\boxed{ans=29}$

By George Coyne

Here is a solution in python but I cannot figure out how to get line numbers

xMax = pow(2,16)    # Don't need to check numbers > 2^16
cnt = 0
solutions = []

for x in range(1,xMax+1):
    x0 = x
    steps = 0
    while steps < 16 and not (x == 1) and (x <= xMax):
        if x % 2 == 1:
            x = 3 * x + 1
        else:
            x = x // 2
        steps += 1

    if x == 1 and steps == 16:
        solutions.append(x0)
        cnt += 1

print("There are {0} solutions: {1}".format(cnt, solutions))

Output: There are 29 solutions: [7, 44, 45, 46, 272, 276, 277, 280, 282, 300, 301, 302, 1536, 1664, 1696, 1704, 1706, 1808, 1812, 1813, 1816, 1818, 10240, 10752, 10880, 10912, 10920, 10922, 65536]

Mathematica one liner:
Count[Array[If[#>1,#0@If[OddQ@#,3#+1,#/2]+1,0]&,2^16],16]

In Mathematica, the code below return 29 (with memoization):

${\text{collatz}[\text{n\$\_\$}]\text{:=}}{\text{collatz}[n]=\text{If}[n==1, 0,\text{If}[\text{Mod}[n,2]== 0, \text{collatz}[n/2]+1,\text{collatz}[3 n +1]+1]];}\\\ {\text{Length}\left[\text{Select}\left[\text{Table}\left[n,\left\{n,2^{16}\right\}\right],\text{collatz}[\#]==16\&\right]\right]}$ )

Gotta love ES6.

I solve it backwards and show the steps each one takes at the end. The numbers make a neat little gradient at the end.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

"use strict";

// Initial condition:
let leaves = [1];
let numSteps = 16;

for(let i=0; i<numSteps; i++){
    let nextLayer = [];
    leaves.forEach((leaf)=>{
        let cache = (leaf-1)/3;
        if(!(cache%1) && cache>1 && (cache%2))  // Integer, >1, odd
            nextLayer.push(cache);
        nextLayer.push(leaf*2);
    });
    leaves = nextLayer;
}

leaves.sort((a,b)=>(a-b));

// For verification purposes:
function collatzify(a){
    let chain = [];
    while(a != 1){
        a = (a%2)?(3*a+1):a/2;
        chain.push(a);
    }
    return chain;
}

leaves = leaves.map((num)=>{
    let retobj = {};
    retobj[num]=collatzify(num);
    return retobj;
})

console.log(leaves);
console.log(`There are ${leaves.length} numbers that take ${numSteps} steps.`)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

% node temp.js
[ { '7': [ 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1 ] },
  { '44': [ 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1 ] },
  { '45': [ 136, 68, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1 ] },
  { '46': [ 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 ] },
  { '272': [ 136, 68, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1 ] },
  { '276': [ 138, 69, 208, 104, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1 ] },
  { '277': [ 832, 416, 208, 104, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1 ] },
  { '280': [ 140, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 ] },
  { '282': [ 141, 424, 212, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 ] },
  { '300': [ 150, 75, 226, 113, 340, 170, 85, 256, 128, 64, 32, 16, 8, 4, 2, 1 ] },
  { '301': [ 904, 452, 226, 113, 340, 170, 85, 256, 128, 64, 32, 16, 8, 4, 2, 1 ] },
  { '302': [ 151, 454, 227, 682, 341, 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1 ] },
  { '1536': [ 768, 384, 192, 96, 48, 24, 12, 6, 3, 10, 5, 16, 8, 4, 2, 1 ] },
  { '1664': [ 832, 416, 208, 104, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1 ] },
  { '1696': [ 848, 424, 212, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 ] },
  { '1704': [ 852, 426, 213, 640, 320, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 ] },
  { '1706': [ 853, 2560, 1280, 640, 320, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 ] },
  { '1808': [ 904, 452, 226, 113, 340, 170, 85, 256, 128, 64, 32, 16, 8, 4, 2, 1 ] },
  { '1812': [ 906, 453, 1360, 680, 340, 170, 85, 256, 128, 64, 32, 16, 8, 4, 2, 1 ] },
  { '1813': [ 5440, 2720, 1360, 680, 340, 170, 85, 256, 128, 64, 32, 16, 8, 4, 2, 1 ] },
  { '1816': [ 908, 454, 227, 682, 341, 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1 ] },
  { '1818': [ 909, 2728, 1364, 682, 341, 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1 ] },
  { '10240': [ 5120, 2560, 1280, 640, 320, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 ] },
  { '10752': [ 5376, 2688, 1344, 672, 336, 168, 84, 42, 21, 64, 32, 16, 8, 4, 2, 1 ] },
  { '10880': [ 5440, 2720, 1360, 680, 340, 170, 85, 256, 128, 64, 32, 16, 8, 4, 2, 1 ] },
  { '10912': [ 5456, 2728, 1364, 682, 341, 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1 ] },
  { '10920': [ 5460, 2730, 1365, 4096, 2048, 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1 ] },
  { '10922': [ 5461, 16384, 8192, 4096, 2048, 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1 ] },
  { '65536': 
     [ 32768,
       16384,
       8192,
       4096,
       2048,
       1024,
       512,
       256,
       128,
       64,
       32,
       16,
       8,
       4,
       2,
       1 ] } ]
There are 29 numbers that take 16 steps.

• By Excel VBA with short simple code:

• Sub Collatz conjecture()
• Dim n, n1, i, j, x, z As LongLong
• x = 3
• z = 200000
• n = 0
• For n1 = x To z
• i = 0
• n = n1
• 1 i = i + 1
• If n > 1 Then If n Mod 2 = 0 Then
• n = n / 2
• Else
• n = n * 3 + 1
• End If
• Else
• GoTo 2
• End If
• GoTo 1
• 2 If i - 1 = 16 Then
• j = j + 1
• ThisWorkbook.Sheets("sheet1").Cells(1, j) = n1 ThisWorkbook.Sheets("sheet1").Cells(2, j) = i - 1
• End If
• Next n1
• ThisWorkbook.Sheets("sheet1").Cells(4, 1) = j
• End Sub

• output:
• • Numbers: 7 44 45 46 272 276 277 280 282 300 301 302 1536 1664 1696 1704 1706 1808 1812 1813 1816 1818 10240 10752 10880 10912 10920 10922 65536

• *counter: 29

The greatest integer that would have n steps is $2^{n}$ (in which case every step would be even, so every step decreases). The next greatest possible value with n steps is $\frac{2^{n-1}-1}{3}$ . To obtain this, you could think about it like this: there are two ways to reach one value (dividing a certain value in half, or multiplying another certain value by 3 and adding 1). To get the highest values, you need to find the two ways to reach $2^{n-1}$ , which takes exactly n-1 steps to get to 1. The first way is to multiply this by 2, giving us our greatest value $2^{n}$ . The other way is subtracting 1 and dividing by 3, giving us $\frac{2^{n-1}-1}{3}$ . The latter value isn't always an integer, but the second greatest integer can't be greater than this value. This is helpful since we know we can stop an iterating program once we've reached this value, and simply append $2^{n}$ to the answer list.

I wrote a Python program that took in a value n, which is the number of steps you are trying to compute for (in this case, 16). It would loop for integers from 1 to $\frac{2^{n-1}-1}{3}$ + 1 (the plus 1 is so that Python includes this value). For each integer, it would keep track of the steps taken according to the Collatz rule, putting the values in a list. If the length of the list exceeded n, it would move on to the next integer. If the list reached the value 1, Python checks if the length of the list is n. If it is, it appends the starting value to a separate list names "ans". At the end of this loop, I append $2^{n}$ since I know this is also a solution, then I print the length of the ans list.

def hail(n): # n is number of steps to reach 1
    ans = []

    for a_0 in range(1, int((2**(n-1)-1)/3) + 1): # Tests all integers from 1 to known bound (before 2^n)
        out = [] # Lists each step for a starting integer
        a = a_0 

        while a != 1:
            if len(out) > n:
                out = [] 
                break
            elif a%2 == 0: # if even, divide by 2
                a = a/2
            else:
                a = 3*a + 1 # if odd, multiply by 3 and add 1
            out.append(a)

        if len(out) == n:
            ans.append(a_0)

    ans.append(2**n)
    print(len(ans))
    return ans

When ran, and calling the function with 16 as the argument, we get:

>>> hail(16)
29
[7, 44, 45, 46, 272, 276, 277, 280, 282, 300, 301, 302, 1536, 1664, 1696, 1704, 1706, 1808, 1812, 1813, 1816, 1818, 10240, 10752, 10880, 10912, 10920, 10922, 65536]

I just cranked it quickly with AWK , without much pre-thinking of the problem (off-the-cuff simplifications, such as 65536 would be the largest integer that would generate a length of 16.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# to get the answer to a puzzle at Brilliant
#
#  How many numbers generate a sequence length of 16?
#

function collatz(a,  count) {
  count=0;

  while ( a > 1 ) {
    if ( a % 2 != 0 ) {
      a = a*3 + 1;
    } else {
      a = a/2;
    }
    count++;
  }
}

BEGIN {
  for ( t=1 ; t <= 100000; t++ ) {
    count = collatz( t );
    counts[count]++;
  }
  print "seq length 16 occurs " counts[16] " times";
  exit(0);
  }

seq length 16 occurs 29 times

Once you figure out that the largest possible number to reach 1 in 16 steps is 2^16 = 65536 things are pretty easy (I tried up to 30 million before i thought of that).

I used Matlab and the broke the while loop function at 17 steps to not fry my laptop. The script should compute the solution within a second. First, write a function for Collatz which takes in a number k and yield the number of steps required to reach 1 (or rather, how many steps, up to 17, does it take to reach 1).

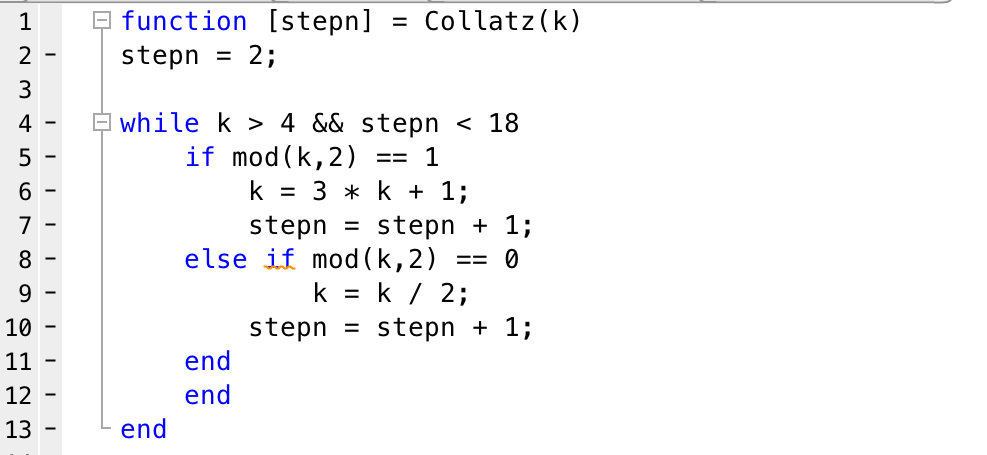
Then we just need a few lines on another script to run our function from 1 to 65536. I used logical arrays to smoothen the elimination process, thanks to Matlab.

Ta da!

Simple brute-force using Python

def collatz(n):
    x = 2
    while n != 4:
        if n % 2 == 0:
            n /= 2
        else:
            n = 3 * n + 1
        x += 1
    return x

n = 0

for i in range(5, 2 ** 16 + 1):
    if collatz(i) == 16:
        n += 1

print(n)

A straight forward (maybe a bit dummy) way to compute this is to check every number up to the largest possible one, which is $2^{16}$ .

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

def measure_steps(x):
    n=0
    while x!=1:
        if x%2:
            x = x*3 + 1
        else:
            x = x/2
        n+=1
        if n > 16:
            break
    return n

def count_steps():
    n=0
    for i in range(2**16):
        if measure_steps(i) == 16:
            #print(i)
            n+=1
    return n

print(count_steps())

The above returns 29, which is the answer !