Appropriate Substitution
x 3 − 6 x 2 + 1 2 x = 8
If a , b , c are the roots of the cubic equation above. And given that for coprime positive integers m , n , we have:
( a 1 + b 1 + c 1 ) 2 = n m
What is the value of 1 6 ( m − n ) ?
The answer is 80.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
There are some minor typos in your solution.
a b + b c + c a = 1 2 = ( − 1 2 ) , a b c = 8 = ( − 8 )
Log in to reply
Sorry.... :)
Log in to reply
Can you update the value of a b c ? You can do so by selecting "Edit" at the bottom of your solution.
Log in to reply
@Calvin Lin – Sorry again....new to brilliant...still not perfect in writing solutions or questions....thanx for helping me out and request you to help me in future as well... :)
hi im not very good at math.. why abc = 8 and ab+bc+ca=12?
The given equation x 3 − 6 x 2 + 1 2 x = 8 is simply the expansion of ( x − 2 ) 3 = 0 .
hence, a = b = c = 2
S o , ( a 1 + b 1 + c 1 ) 2 = n m = 2 2 3 2 = 4 9
Therefore, 1 6 ( m − n ) = 1 6 × ( 9 − 4 ) = 8 0
I would have used the same method as Sakanksha Deo if the equation would have been a bit different but the given equation is a simple one therefore not proceeded that way.
a,b,c are the roots From the eqn ab+bc+ac=12,abc=-8 (1/a + 1/b + 1/c)^2=((ab+bc+ac+)/abc)^2=(12/-8)^2=(-3/2)^2=9/4 9/4=m/n m=9,n=4 16(m-n)=16(9-5)=16(5)=80
x^3 - 6x^2 + 12x - 8 = 0 ; (x-2)^3 = 0 ; x = 2 ; all the three root are equal and its 2 ; so a = 2; b = 2; c = 2 ; (1/a + 1/b + 1/c)^2 = 9/4 = m/n ; m = 9; n = 4; 16(9-4) = 80
or else replace x by 1/x :P so that the roots are multiplicative inverse of themselves ..!:P
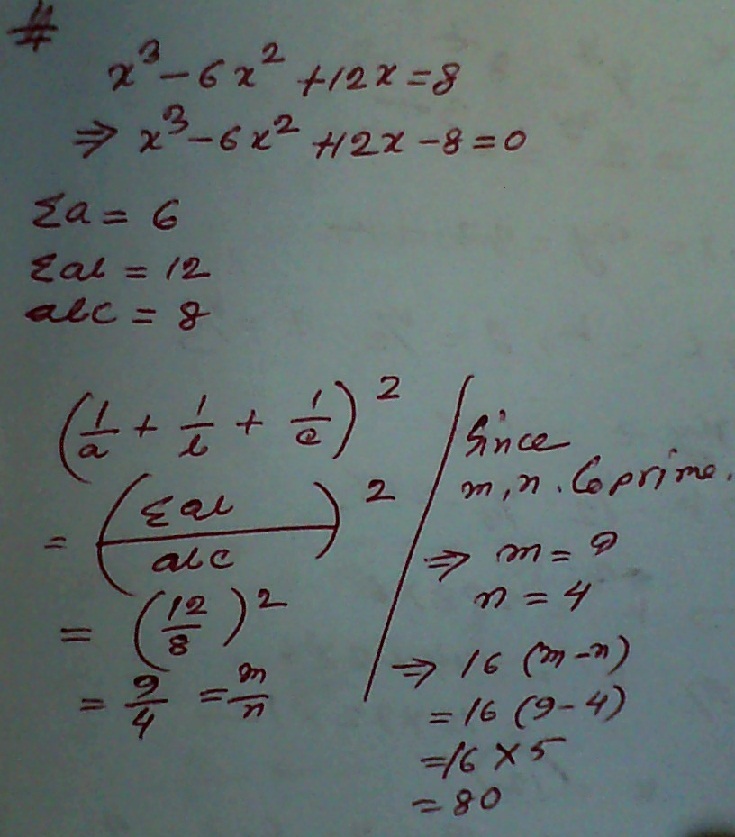
First method - direct and easy method
( a 1 + b 1 + c 1 ) 2
= ( a b c b c + a c + a b ) 2
Now,
We know that,
a b c = − 8 a b + b c + a c = 1 2
Therefore,
= ( a b c b c + a c + a b ) 2
= ( 8 1 2 ) 2 = n m
= ( 2 3 ) 2 = n m
Therefore,
1 6 ( m − n ) = 8 0
Second method - a bit concept based one
The equation who's roots will be a 1 , b 1 , c 1 is,
8 x 3 − 1 2 x 2 + 6 x − 1 = 0
Now,
Sum of roots = a 1 + b 1 + c 1 = 8 1 2
= 2 3
Therefore,
n m = ( 2 3 ) 2 = 4 9
Therefore,
1 6 ( m − n ) = 8 0