It will drill your mind... be ready!
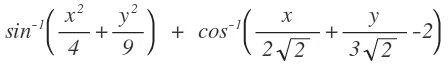 If the value of the given expression is a, then what is
⌊
a
⌋
?
If the value of the given expression is a, then what is
⌊
a
⌋
?
Details And Assumptions:
-
x , y are cartesian plane co-ordinates.
-
Expression given here is a real-valued one, not complex-valued.
-
s i n − 1 x , c o s − 1 x are defined on [ − 1 , 1 ]
Try more Trigonometry Problems
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Thanks. Can you explain why those are the only permissible values?
Log in to reply
Because
− 1 ≤ 4 x 2 + 4 y 2 ≤ 1
&
− 1 ≤ 2 . 2 x + 3 . 2 y − 2 ≤ 1
So the upper one is the area bounded within or on the boundary of the ellipse and the lower one.ie. a line is the tangent to the ellipse at x = 2 and y = 2 3 . If you will put any values of x and y other than this one, that will go out of the domain of the given inverse function. You can also checkout by putting some values other than this. I could better clarify it using the figures of ellipse and straight line. Anyway, i hope you will get what i want to convey .
Log in to reply
Did the same
What if the domain is converted to something visual? Like ya see, the input in arcssine depicts an ellipse with a point (x,y) on it, while that of arccos depicts another ellipse with point (sqrt(x), sqrt(y)) on it.
Further, this will through out arcsin(1) + arccos(-1) = 2 3 p i
Affirmative?
Log in to reply
@A Former Brilliant Member – What do you mean by another ellipse with points x and y on it?
@Calvin Lin Sir , I have posted my solution above , can you please have a glance at it and suggest necessary changes , if any.
That was my method of solution, as well. Well played!
− 1 ≤ 2 2 x + 3 2 y − 2 ≤ 1
⇒ 1 ≤ 2 2 x + 3 2 y ≤ 3
⇒ 1 ≤ 2 ( 2 x + 3 y ) 2 ≤ 9
By Cauchy - Schwartz Inequality ,
( 4 x 2 + 9 y 2 ) ( 1 + 1 ) ≥ ( 2 x + 3 y ) 2 ⇒ 4 x 2 + 9 y 2 ≥ 1
Also , by definition of s i n − 1 function 4 x 2 + 9 y 2 ≤ 1
⇒ 4 x 2 + 9 y 2 = 1
And hence equality holds in the Cauchy Inequality statement also and hence x = 2 , y = 2 3
Plugging in the values gives desired answer as 2 3 π
There is a false line in your solution. It doesn't affect the rest of the proof because it is not necessary.
Be careful when people say "It is easy to see that" or "It is obvious that". Sometimes, it is a claim that they don't know how to prove, and think it has to be true.
Log in to reply
The proof is like - If any of the terms 2 2 x , 3 2 y is negative , then the other has to be greater than 1 , like 2 2 x > 1 ⇒ x > 2 2 ⇒ 4 x 2 > 1 which is not allowed.(Likewise for 3 2 y )
Does that work?
Log in to reply
Sure, that's one way of doing it. And you should make it clear that you're using both equations, since up to that point in time you have only been using one of them.
Also, note that you do not require the terms to be positive when applying Cauchy Schwarz.
Log in to reply
@Calvin Lin – Right , I missed that point ! , I have edited my solution.
The argument of arc sine somehow gives a hint. Take an ellipse and its tangent at eccentric angle 45°. I don't know why it works but it gave the answer as 3π/2.
Use the domains of the inverse functions x / 2 √ 2 + y / 3 √ 2 − 2 > = − 1 so x / 2 + y / 3 > = √ 2 .and x 2 / 4 + y 2 / 9 < = 1 Using the trivial inequality a 2 + b 2 > = ( a + b ) 2 / 2 set a = x / 2 and b = y / 3 .You get x 2 / 4 + y 2 / 9 > = ( x / 2 + y / 3 ) 2 / 2 > = ( √ 2 ) 2 / 2 so we get x 2 / 4 + y 2 / 9 > = 1 .Now compare the two inequalities clearly equality holds.the term ( x 2 / 4 + y 2 / 9 = 1 ) So x / 2 = y / 3 and x = √ 2 , y = 3 / √ 2
Log in to reply
Yeah did the same!
It really demonstrates how we can deal with ellipses efficiently by making these substitutions!
Great explanation!!!!!!!
let x = 2 sin θ , y = 3 cos θ . Substituting the values we get π / 2 + arccos sin ( π / 4 + θ ) − 2 as domain of inverse of cosine lies between [ − 1 , 1 ] . sin ( π / 4 + θ ) will have value 1. henceforth π / 2 + π = 3 π / 2 ⌊ 3 π / 2 ⌋ = 4
Moderator note:
I'm not sure what you're doing here.
Why we are allowed to make the substitution in the first line? Are we allowed to assume that 4 x 2 + 9 y 2 = 1 ? If so, why?
If we find the domain of the given function corresponding to the inverse trigonometric functions..the only permissible value is x = 2 and y = 2 3 . Putting the above permissible values of x and y in the given expression , we get the expression equal to 2 3 π .
So ⌊ 2 3 π ⌋ = 4