Involving Involutions

The function $f(x) = \frac ax$ is an example for all real $a \neq 0$ since

$f(f(x)) = \frac a {\frac a x} = \frac {a {\color{#D61F06} \cdot x}} {\frac a x {\color{#D61F06} \cdot x}} = \frac {ax} a = x$ .

Consider a new function $g(x) =h(f(h^{-1}(x)))$ , with $f(x)$ being an involution and $h(x)$ being any function with an inverse. $g(g(x)) = h(f(h^{-1}(h(f(h^{-1}(x)))))) = h(f(f(h^{-1}(x)))) = h(h^{-1}(x)) = x$ Thus, $g(x)$ is also an involution. Since there are infinitely many invertible functions, there must be infinitely many involutions.

A one-dimensional involution can be interpreted graphically as any function which is symmetric over the line $y=x$ . For instance, you can take any continuously differentiable even function $g(x)$ such that $|g'(x)| < 1$ for every $x$ . Then rotate its graph $45^\circ$ clockwise and you'll end up with the graph of an involution.

Using this construction, the functions given in the problem are $g(x) = \frac{a}{\sqrt{2}} \implies f(x) = a-x \\ g(x) = \sqrt{2 + x^2} \implies f(x) = 1/x \\ g(x) = \sqrt{2+x^2} + \sqrt{2} \implies f(x) = \frac{x}{x-1}$

It should be apparent that there are infinitely more $g(x).$ For instance, we could use

• $g(x) = \sqrt{a+x^2} + b$ where $a>0$
• $g(x) = a\cos(bx) + c$ where $|ab| < 1$
• etc.

The simplest function not on your list is the identity function: $f(x)=x$

Any function that has $y=x$ as a line of symmetry also works.

Any homographic function $f(x)=\dfrac{{\color{#3D99F6}{a}}x+b}{cx+{\color{#D61F06}{d}}}$ , $\quad (c\ne0, \; ad\ne bc)$ , is an involution, iff ${\color{#3D99F6}{a}}+{\color{#D61F06}{d}}=0$ .

Consider the function $f(x)=\frac{x+a}{x-1}$ , where $a$ is any real. Now, find $f(f(x))$ : $f(f(x))=\dfrac{\frac{x+a}{x-1}+a}{\frac{x+a}{x-1}-1}$ Multiplying $a$ (in the numerator) and -1 (in the denominator) by $\frac{x-1}{x-1}$ : $\dfrac{\frac{x+a}{x-1}+\frac{ax-a}{x-1}}{\frac{x+a}{x-1}+\frac{-x+1}{x-1}}=\dfrac{\frac{x(a+1)}{x-1}}{\frac{a+1}{x-1}}=\frac{x(a+1)}{a+1}=x$ Therefore, since $a$ can be any real, there are uncountably infinitely more solutions. $\beta_{\lceil \mid \rceil}$

for any a f(x)=a-x is an example

f(x)=a-x

f(f(x))= a-(a-x)) = a-a+x = x

Suppose we have such a function, $f(x)$ . As is commonly done to functions, let's look at this one as a relationship on the x-y plane. $f(x)$ being an involution means that for every $x$ we plug in, we can take the corresponding $y$ , plug it back in, and out comes that same $x$ value we started with. If you pick enough $x$ 's and make up enough $y$ 's... 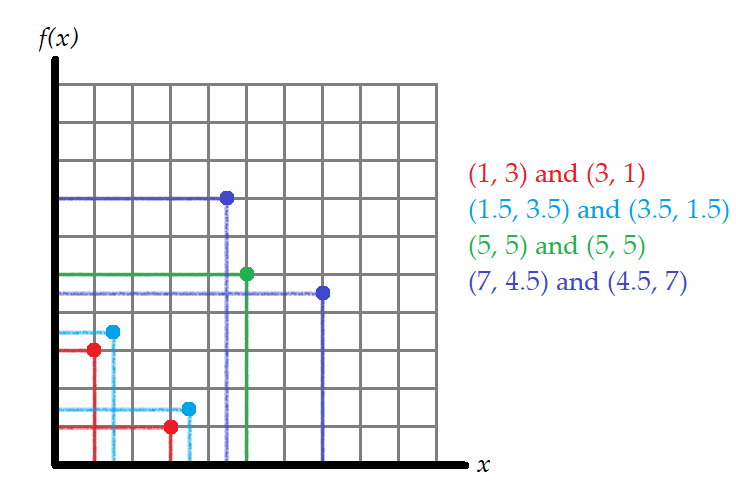You might notice some kind of mirror symmetry in the picture. But all we need in order to argue that there's infinitely many involutions is this: Imagine the function being built two points at a time, starting at say, $x=0$ . We can make up any corresponding $y$ value for $x=0$ . And as soon as we get the point $(0, something)$ , we also get a second point $(something, 0)$ . We move a little bit to the left of 0, getting two new points. Then we move a little bit to the right of 0, getting two more points. We do this for every number on the $x$ axis, and we have our involution. But since we made up each $y$ value, we had infinitely many choices for a function, no matter how strange-looking.

The family of functions f(x)=a^(1/(log base a of x)) are all involutions, since a^1/log base a of (a^1/log base a of x)=a^log base a of x=x.

In mathematics there exists infinite no. Of invertible functions. Here are just pool of three enlisted.

In fact h(f(x))=x holds if the function h is inverse of f. Inverse functions have property that they are symmetric about y=x.Here we have f in place of h so any function which is symmetric about y=x will hold this property.

I don’t know this type of math. I guessed the right answer :P hahahahahahahaaha.

If a function is an involution, then (from the definition given in the problem) it is its own inverse.

Remember that the graphs of a function and its inverse are mirror images in the line $y=x$

So any function which is symmetrical in the line $y=x$ is its own inverse, and therefore is an involution.

There are infinitely many such graphs. For example, any of the lines perpendicular to $y=x$ will do, so

$y=-x+a$ represents an infinite family of invloutions.

Let's illustrate this with a specific example. Let's choose $y(x)=-x+3$ and $x=7$ . Then

$y(y(7))=-y(7)+3=-(-7+3)+3=-(-4)+3=4+3=7$

Since we have found an infinite family of involutions (and there other such families) we can certainly say

$\boxed{\text{There are an infinite number of involutions}}$

All functions $f(x) = \frac {1}{x^k}$ are example of it

For any $A \subset \mathbb{R}_{+}$ , the function $f$ defined by $f(x) = -x$ if $x \in A$ or $-x \in A$ and by $f(x) = x$ otherwise, is an involution.

Just take

• f(x) = x for all x exept for :

• f(a) = b

• f(b) = a

The first function 1/x will also work with any value (e.g. 2/x, 3/x, 4/x ....)

A function, $f(x)$ , is another function, $g(x)$ 's inverse iff you get the graph of $g(x)$ when you reflect the graph of $f(x)$ over the line $x=y$ . This means that for a function to be an involution, it has to remain the same when reflected over the line $x=y$ . It is obvious that there are infinitely many graphs of this type that aren't of the form $a-x$ . Therefore, there are infinitely many more involutions than the examples provided.

If $f(x)=n$ then $f(f(x))=f(n)$ wich is $n$ .

Root of x ^2