Iota Forever
Evaluate the real part of the number i i i . . . .
Note: i is the imaginary number − 1
The answer is 0.438.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
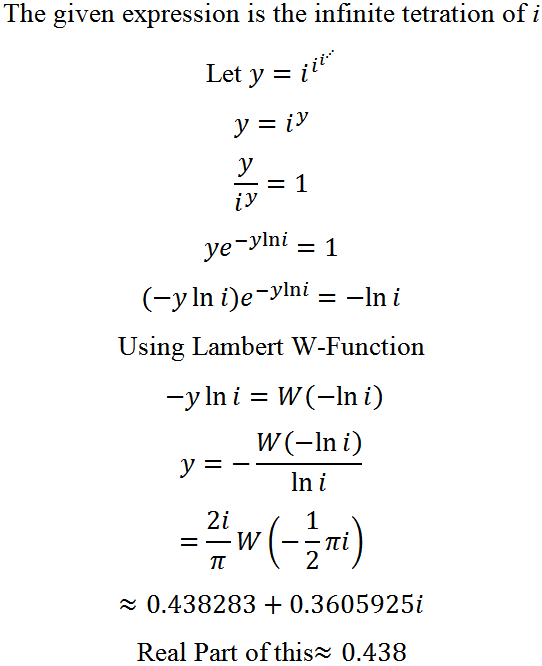
Log in to reply
whats lambert function......... plz reply..
Log in to reply
Lambert W function ... basically it's a special function: to find the inverse of W e W = f ( w ) . That is, if you have an equation x e x = 1 2 3 4 5 , then the value of W ( 1 2 3 4 5 ) is simply the root of the previous equation. Simplest way to solve it is by numerical / approximation method.
Log in to reply
@Pi Han Goh – I saw the solution to the above posted duplicate question.. I had made the equations , but he writes using numerical methods we get value of a and b........ plz sorry to disturb you, thanks.......... could you explain
Log in to reply
@Rajat Kharbanda – See equation 12 here , set x = − 2 1 π i .
Log in to reply
@Pi Han Goh – gone over my head...... but thanks anyway
@Pi Han Goh – nice explanation sir, but would you please show me a proof that the infinite tetration converge only when e − e ≤ x ≤ e e 1
Log in to reply
@Digvijay Singh – Hint: what's the extreme values of x x 1 ?
Log in to reply
@Pi Han Goh – its e 1 / e , but how is this connected to the convergence?
Log in to reply
shit...! i did'nt knw... sorry... should i remove this now (the question)?
Log in to reply
It's up to you. I would have removed it if I were you.
Let i i i . . . = x
∴ x = i x
Differentiating both sides with respect to x :
1 = i x ⋅ l o g e i
⟹ 1 = x ⋅ l o g e i
⟹ x = l o g e i 1 = i . π 2
So, real part of x is 0 .
What's wrong with it ? @Digvijay Singh
i i i . . . = A + B i = i A + B i ⇒ e 2 π i ( A + B i ) = e − 2 π B e 2 π A i = A 2 + B 2 e tan − 1 A B i
⎩ ⎨ ⎧ e − 2 π B = A 2 + B 2 2 π A = tan − 1 A B ⇒ A 2 + B 2 = e − π B ⇒ tan 2 π A = A B ⇒ B = A tan 2 π A . . . ( 1 ) . . . ( 2 )
Substituting Eqn. 2 in Eqn. 1:
A 2 + A 2 tan 2 2 π A = e − π A tan 2 π A
Using numerical method, we find that A = 0 . 4 3 8 2 8 2 9 3 7
What do you mean by
numerical method
?
Log in to reply
I used Excel spreadsheet to calculate f ( A ) = A 2 + A 2 tan 2 2 π A − e − π A tan 2 π A . I first estimated a value for A , A 1 then I checked for f ( A 1 ∗ ) ≈ 0 , then estimated a more accurate value for A , A 2 and continued to about A 1 0 .
Log in to reply
I plotted the graph. Just wondering if there's a method without using calculator/computer.
Log in to reply
@Pranjal Jain – I plotted the graph too to check the f ( x ) ≈ 0 but with a spreadsheet. If the equation can be easily differentiated, we can use Newton's Method x n + 1 = a n − f ′ ( x n ) f ( x n ) . Numerical method usually needs calculator/computer.
Log in to reply
@Chew-Seong Cheong – Sir, while using newtons meathod, What to take x o initially? How to know what to take?
Log in to reply
@Md Junaid – Usually any near estimate will work.