Irodov problem; ODE solving practice

Classical Mechanics Level 2

Difficulty: Not hard. It's pretty easy conceptually; the only not-so-easy part is integrating for velocity

So, I kind of jumped late onto the Irodov bandwagon, and I decided to solve some problems today.

Here's the problem:

A bar of mass $m$ resting on a smooth horizontal plane starts moving due to the force $\displaystyle F = \frac{mg}{3}$ of constant magnitude.

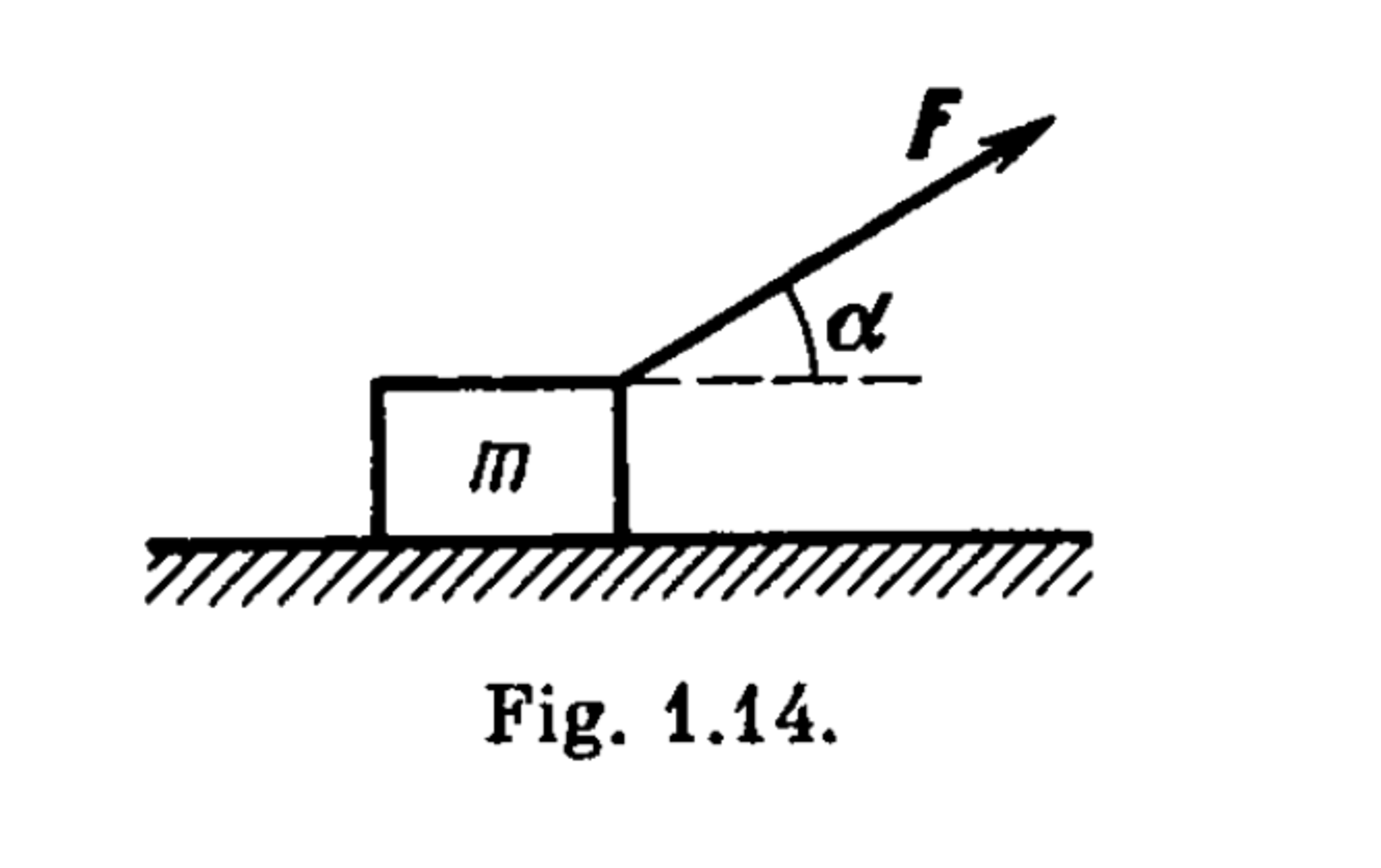
Note that in the diagram the angle is labelled as $\alpha$ , but to not confuse you between $\alpha$ and $a$ , I have given it as $\theta$ . While in one dimensional motion, the angle $\theta$ between the direction of this force and the horizontal varies as $\theta = ax$ , where $a$ is a constant, and $x$ is the distance traversed by the bar from its initial position.

Find the velocity of the bar as a function of the angle $\theta$ .

The answer comes in the form:

$\displaystyle v(\theta) = \sqrt{\frac{p}{q}\frac{g \sin(\theta)}{a}}$

Where $p$ and $q$ are co-prime positive integers. Type the value of $p+q$ into the answer box.

By the way, since Irodov's problem solutions are all over the internet, don't go around looking for them before you solve the problem. It'll only take 5 minutes to solve this one.

The answer is 5.

1 solution

Talulah Riley
Sep 20, 2020

Write the basic equations
Vertical direction: $N+\frac{mg}{3} \sin \theta=mg$
Horizontal direction: $F=\frac{mg}{3} \cos \theta$
Which gives $a_{x} =\frac{g}{3} \cos \theta$ Note that $\theta= ax$
$\int_{0}^{v} vdv=\frac{g}{3} \int_{0}^{x} \cos (ax)dx$
Integrating and substituting the limits gives: $v^{2}=\frac{2g}{3a} \sin (ax)$
$v=\sqrt{\frac{2g}{3a} \sin \theta }$

@Lil Doug Too easy bro. Nice one. You've done Irodov, haven't you?

Krishna Karthik - 8 months, 3 weeks ago

Unfortunately, I have solved the whole mechanics section of Irodov, so this problem is very common.

Talulah Riley - 8 months, 3 weeks ago

Haha lol. Nice. I only just started doing Irodov.

Krishna Karthik - 8 months, 3 weeks ago

@Krishna Karthik Nice bro. Keep going and keep posting, it will be like a revision for me, so it will be a benefit for me also.

Talulah Riley - 8 months, 3 weeks ago

@Lil Doug While Irodov is not easy, it's a piece of cake compared to your Pathfinder problems.

Edit: I actually take back what I said. The majority of Irodov is quite hard.

Krishna Karthik - 8 months, 3 weeks ago

@Krishna Karthik Yeah Pathfinder is also easy too.

Talulah Riley - 8 months, 3 weeks ago

Well, I mean it's not super hard, but what's the problem sheet with your momentum conservation problems that you sent to me?

That was pretty hard imo.

Krishna Karthik - 8 months, 3 weeks ago

@Krishna Karthik – @Krishna Karthik yeah, maybe.
bye I am having date with my girlfriend today.

Talulah Riley - 8 months, 3 weeks ago

@Lil Doug Btw, where do you get your Classical Mechanics problems that you post nowadays regularly? Those ones are quite tough.

Krishna Karthik - 8 months, 3 weeks ago

@Lil Doug Imagine being that one person who got this problem wrong🤣

Krishna Karthik - 8 months, 3 weeks ago

Irodov problem; ODE solving practice

The answer is 5.

1 solution

0 pending reports