Irrationally, Can This Happen?

Number Theory Level 4

True or False?

The infinite sequence $\big\lfloor 1\times \sqrt{ 2017 } \big\rfloor,\ \big\lfloor 2 \times \sqrt{ 2017 } \big\rfloor,\ \big\lfloor 3 \times \sqrt{ 2017 } \big\rfloor,\ \big\lfloor 4 \times \sqrt{ 2017 } \big\rfloor,\ \ldots$ contains infinitely many perfect squares.

Notation: $\lfloor \cdot \rfloor$ denotes the floor function .

True False

3 solutions

Calvin Lin Staff
Jun 16, 2017

Claim: There are (infinitely many) solutions to the pell's equation $x^2 - 2017 y^2 = - 1$ .

Corollary: For each of these solutions, $0< xy \sqrt{2017} - x^2 = \frac{ x } { y \sqrt{ 2017} + x } = \frac{ x} { \sqrt{ x^2 + 1 } + x } < \frac{1}{2} .$

Hence, $\lfloor xy \sqrt{2017} \rfloor = x^2. _ \square$

Of course, these do not necessarily describe all of the possible solutions, nor is this the only way to prove this problem. For example, M Zadeh found that the smallest perfect square is $\lfloor 97 \sqrt{2017} \rfloor = 66^2$ , which is much smaller than the initial solution $x_1 y_1$ below. I would be interested in seeing alternative solutions, esp if they can help generalize the problem.

Proof of claim
I do not know of a simple proof of the claim. Here are 2 rigorous justifications that the base solution exists:

From the theory, $x^2 - ny^2 = -1$ has solutions if and only if the continued fraction of $\sqrt{n}$ has odd length. We can verify that the continued fraction of $\sqrt{2017}$ has 51 coefficients, hence it has solutions. (There is no known classification for such numbers, so this has to be checked manually.)
Find (with the help of a solver) the initial solutions of $x_1 = 106 515299 132603 184503 844444, y_1 = 2 371696 115380 807559 791481$ .

We can then find infinitely many solutions (in fact, all solutions) by setting $x_n + \sqrt{ 2017 } y_n = ( x_1 + \sqrt{ 2017} y_1)^{2n-1}$ .

Generalization : For every irrational number $r$ , the sequence $B_r = \{ \lfloor nr \rfloor \}$ is known as the Beatty Sequence . For any non-constant polynomial $f$ with integer coefficients, the sequence $B_r$ (for an irrational $r$ ) contains infinitely many number of the form $f(n)$ .

Lemma: Let $\{ x \}$ denote the fractional part of $x$ . Then, $m \in B_r \Leftrightarrow 1 - \frac{1}{r} < \{ \frac{m}{r} \}$

Proof: $m \in B_r \Leftrightarrow m = \lfloor nr \rfloor \Leftrightarrow m < nr < m+1 \Leftrightarrow \frac{m}{r} < n < \frac{ m}{r} + \frac{1}{r} \\ \Leftrightarrow n - \frac{1}{r} < \frac{m}{r} < n \Leftrightarrow 1 - \frac{1}{r} < \{ \frac{m}{r} \}. \, _\square$

Claim: A result of Weyl states that for any irrational $r$ and any non-constant polynomial $f$ with integer coefficients, the sequence $\{ f(n) \times r \}$ is equidistributed in $[0, 1 ]$ , and hence dense.
(Note: I do not know how to prove this claim.)

The proof of the generalization follows immediately. Since $\{ f(n) \times r \}$ is dense, there are infinitely many values in $( 1 - \frac{1}{r} , 1 )$ . For each of these values, it follows from the lemma that $f(n) \in B_r$ .

Moderator note:

Beatty Sequences show up in a surprising way in combinatorial game theory. I'm going to explain the game, but I won't spoil the fun of working out the connection. (If you want to learn more, a whole quiz about this particular game is coming soon in the Logic Exploration .)

A pet shop has a certain number of puppies and kittens. You are playing a game with a single opponent where on each round you can take either some number of puppies, some number of kittens, or an equal number of puppies and kittens. The last person to take a pet wins. Given best play, what's the optimal strategy to win?

I would be interested in seeing alternative solutions, esp if they can help generalize the problem.

I suspect that $\lfloor r n \rfloor$ contains infinitely many perfect squares, for any irrational number $r$ . (And of course, for all rational $r$ too.)

The intuitive idea is to consider walking on the number line, each time taking a step of length $r$ . If we have enough gaps of the form $x^2 \rightarrow x^2 + 1$ that are not too periodic, then we should fall into them eventually. However, I'm been unable to rigorize this concept. Thinking about this gap is also what caused me to think about Pell's equations.

Calvin Lin Staff - 3 years, 12 months ago

Not quite the statement that you want, but a somewhat weaker statement can be proved easily. Let's assume that $0<r <1$ . It is well known that, for the given irrational $r$ , there exist infinitely many pair of integers $a, b, a<b$ such that $|r-\frac{a}{b}| \leq \frac{1}{b^2}.$ Now take $n=ab$ . This gives $a^2-\frac{a}{b}\leq nr \leq a^2+\frac{a}{b}.$ Since $0<\frac{a}{b}<1$ , we have, $\lfloor nr \rfloor \in \{a^2, a^2-1\}$ . In other words, for any irrational number $0<r <1$ , either $\lfloor nr \rfloor$ or, $\lceil nr \rceil$ is a perfect square for infinitely many $n$ . $\blacksquare$ .

Abhishek Sinha - 3 years, 11 months ago

Unfortunately, the assumption that $0 < r < 1$ makes the sequence $\lfloor r n \rfloor$ give the set of all positive integers, and hence the conclusion is trivial.

Relaxing the constraint on $r$ would widen up the range, and we have something like $a^2 - \lfloor r \rfloor \leq nr \leq a^2 + \lfloor r \rfloor$ . It is through pell's equations of setting $a^2 - 2017 b^2 = {\color{#D61F06} -1 }$ that we obtain an inequality like $0 < \sqrt{2017} - \frac{a}{b} < \frac{ 1 } { 2 \sqrt{ 2017} b^2 }$ , from which we conclude that $a^2 {\color{#D61F06}+ 0} \leq ab \sqrt{2017} \leq a^2 {\color{#D61F06}+ \frac{1}{2} }$ . As you can see, the denominator gives us the size restriction that is necessary. As a side note, we could also solve for $x^2 - 2017y^2 = - 2$ , though no other constant would work.

Note: These 2 ideas are related. The partial continued fractions give the best rational approximation of a real number.

This showcases some of the various issues that I've been running into when trying to track down the "gap". Ultimately, I suspect that a generalized statement would provide a much more satisfying answer.

Calvin Lin Staff - 3 years, 11 months ago

@Calvin Lin – I don't understand your first statement. Of course, $\lfloor nr \rfloor$ are all integers, as it is a floor function, but here we are looking for perfect squares and not any arbitrary integers. Why does the conclusion become trivial then?

Secondly, although I don't have a rigorous proof, I think the proof can be generalized. Note that, in the above, we have taken the sequence $n=ab$ , where $a,b$ may be arbitrarily large. Given any arbitrary irrational number $r$ , we can scale it by some integer $K$ , so that $r'=\frac{r}{K} <1$ . We can now apply the above proof for $r'$ . Hence, the sequence $\frac{ab}{K}r$ have the above property. Now, the proof will follow if we can take a subsequence where $K|b$ , but it requires more work.

Abhishek Sinha - 3 years, 11 months ago

@Abhishek Sinha – I am saying that when $0 < r < 1$ , then $\{ \lfloor nr \rfloor \}$ is the set of all non-negative integers. IE $\{ \lfloor nr \rfloor \} = \mathbb{N} ^ { \geq 0}$ . Hence, there are infinitely many of them which are perfect squares.

It seems like you interpreted the statement as " $\lfloor rn \rfloor$ are positive integers", or that $\{ \lfloor nr \rfloor \} \subset \mathbb{N} ^ { \geq 0 }$ .

Unfortunately, the scaling doesn't quite work as you would like it to. See the rest of my comment for how the coefficient of the denominator affects the bounds. In particular, we need the bound to be something like $| \frac{ a}{ b} - r | < \frac{ 1 } { r b^2 }$ , in order to conclude that $| a^2 - abr | < 1$ . (This is because $a \approx r b$ , and so you see how the multiplication by $ab$ pulls through).

In fact, if this is true, then that suggests a place to look for a counter example, namely pick a large enough $r$ such that we do not have infinitely many rational approximations that perform "well".

Calvin Lin Staff - 3 years, 11 months ago

@Calvin Lin – I see. Thanks

Abhishek Sinha - 3 years, 11 months ago

Once a trivial solution $(x_0 , y_0)$ is found, $x_n , y_n)$ satisfies the negative Pell's equation too, where

$x_n + y_n\sqrt{2017} = (x_0 + y_0\sqrt{2017})^{2n-1}$ .

If the pair $(x_0, y_0)$ is minimal, then these are in fact all the solutions.

Shourya Pandey - 3 years, 11 months ago

[This comment has been summarized in the solution.]

Here is a potential start of an (incomplete) alternative proof which generalizes

The sequence $B_r = \{ \lfloor nr \rfloor \}$ is known as the Beatty Sequence .

Claim: $m \in B_r \Leftrightarrow 1 - \frac{1}{r} < \{ \frac{m}{r} \}$ (the notation means fractional part)

Thus, the statement is equivlaent to saying that the set of $n$ such that $\{ \frac{n^2}{r} \} > 1 - \frac{1}{r}$ is infinite.

We know that the set of $m$ such that $\{ \frac{m}{r} \} > 1 - \frac{1}{r}$ is infinite, because $\{ \frac{m}{r} \}$ is dense in $[0, 1 )$ (for irrational $r$ ), by the standard pigeonhole argument.

However, I can't quite extend it to perfect squares as yet. Here is an attempt. Consider the pigeons $\{ \frac{ n^2 } { r } \}$ for $n = 1$ to $\lceil r \rceil + 1$ , and the holes the intervals $( 1 - a \frac{1}{r} , 1 - (a-1) \frac{1}{r} ]$ for $a = 1$ to $\lceil r \rceil$ . Then, at least 2 of them fall into the same hole.

Ah ... it's a result by Weyl ... Let me write this up.

Claim: $m \in B_r \Leftrightarrow m = \lfloor \left( \lfloor \frac{m}{r} \rfloor + 1 \right) r \lfloor$

Proof: $m = \lfloor \left( \lfloor \frac{m}{r} \rfloor + 1 \right) r \lfloor \Leftrightarrow m < \left( \lfloor \frac{m}{r} \rfloor + 1 \right)r < m + 1 \Leftrightarrow \frac{m}{r} < \left( \lfloor \frac{m}{r} \rfloor + 1 \right) < \frac{m+1}{r}\\ \Leftrightarrow \lfloor \frac{m}{r} \rfloor + 1 - \frac{1}{r} < \frac{m}{r} < \lfloor \frac{m}{r} \rfloor + 1 \Leftrightarrow 1 - \frac{1}{r} < \{ \frac{m}{r} \}$ .

Calvin Lin Staff - 3 years, 11 months ago

I was wondering whether the answer would change if we consider a base other than 10?

Rodion Zaytsev - 3 years, 11 months ago

No it wouldn't. See the proof of the generalization, which is independent of base chosen.

Calvin Lin Staff - 3 years, 11 months ago

M Zadeh
Jun 25, 2017

This may be considered a sort of a solution using logic: I made an Excel spreadsheet to try to find all n<1000 that meet the criterion. The solutions were n=97,501,621, and 787. So one could make an argument if there are this many solutions under n=1000, there must be infinity of them!

A note: I acknowledge that this is not a formal mathematical proof, but as a puzzle solver who had to find the correct true/false answer, using this approach completely satisfied me that the answer is "true".

Finding several solutions does not imply that there are infinitely many of them.

There currently isn't a "logic" to this approach. Perhaps, you can identify what is special about these values of $n$ , to find an infinite family of solutions.

Calvin Lin Staff - 3 years, 11 months ago

I have edited my "solution" to reflect Calvin's comment.

M Zadeh - 3 years, 11 months ago

Solutions for n < 1000000 (this does not prove anything other than there are solutions)

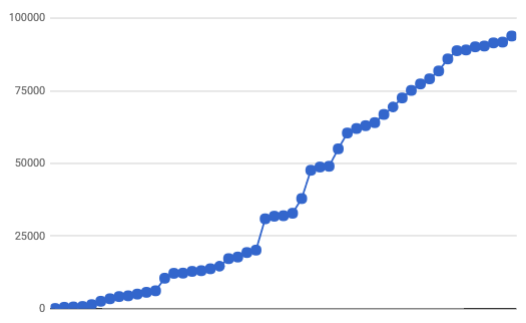
97, 501, 621, 787, 1414, 2574, 3439, 4194, 4449, 5045, 5173, 5656, 6184, 10509, 12193, 12259, 12861, 13099, 13756, 14645, 17243, 17796, 19341, 20180, 30951, 31850, 32010, 32870, 37920, 47658, 48772, 49036, 55024, 60473, 62024, 62994, 64047, 66872, 69443, 72544, 75139, 77364, 79117, 81826, 85975, 88798, 89065, 90137, 90406, 91486, 91757, 93848, 109737, 120363, 123804, 127400, 134418, 135185, 148673, 149595, 158615, 160642, 168511, 174069, 182894, 185327, 186614, 189981, 200931, 208356, 212738, 219956, 220096, 223187, 230722, 236782, 243362, 253326, 259674, 275731, 277772, 278559, 286650, 297781, 324068, 337455, 338496, 342676, 343725, 343900, 355192, 376673, 377406, 381819, 391842, 403131, 448490, 470949, 475054, 476701, 483110, 486851, 492699, 495006, 519017, 531127, 557993, 578691, 590098, 603006, 612078, 632085, 638746, 648082, 684374, 685609, 714069, 717604, 725971, 741308, 751363, 759924, 760965, 771152, 794919, 799182, 810158, 833424, 849301, 850952, 870889, 879824, 880664, 884028, 889086, 892466, 895570, 919737, 922888, 924609, 924896, 940749, 956153, 958489, 961413, 975805, 981710, 984077, 993276, 998637

Leigh Thompson - 3 years, 11 months ago

That's much bunchier than I would have expected it to be, especially given the equidistribution result.

Calvin Lin Staff - 3 years, 11 months ago

Kevin Tong
Jul 1, 2017

If you think about it, the series goes through an infinite amount of integers using the floor function of multiples of $\sqrt{2017}$ . Using the square root of $2017$ is not restricting the result being a perfect square, therefore, among the infinite number of integers produced by the series, there must be an infinite amount of perfect squares. Note: infinity is not a number. For example, there are an infinite amount of integers, an infinite amount of even numbers and an infinite amount of odd numbers. Infinity is just a figure to show that the amount goes on forever.

Unfortunately, your logic does not work. For example, the infinite sequence of $n^2 + 1$ only has 1 perfect square. Having infinitely many integers doesn't guarantee that infinitely many of them will be perfect squares.

What is true though, is that if there are finitely many (not necessarily infinite) subsequences whose (not necessarily distinct) union is the integers, then at least one of the subsequences contains infinitely many perfect squares.

Calvin Lin Staff - 3 years, 11 months ago

True, the infinite sequence $n^2+1$ only has 1 perfect square in it, but that's because the sequence restricts all but 1 perfect square from being produced $n=0$ (Since the sequence is adding 1 to a perfect square). Whereas, in the given sequence, $\sqrt{2017}$ can be thought of as a constant $C \approx 44.9$ . This sequence now simplifies to $\lfloor n \cdot C \rfloor$ . Through a program I created, I was able to generate a number of perfect squares from the sequence, including at $n=97, 501, 621$ . Because $\sqrt{2017}$ is a constant and the sequence is simply taking multiples of that constant, there is nothing restricting the generation of perfect squares. Not only that, but also, if there is an n that generates a perfect square in the sequence such that $n=a \cdot 10^{b} ,C \cdot n = x+y(10^{-z}):x \in \Z, b<z$ , we would be able to generate another perfect square simply by squaring n. Therefore, through the obtained values of n, we may be able to generate even more perfect squares in the sequence simply by squaring n.

Kevin Tong - 3 years, 11 months ago

Because $\sqrt{2017}$ is a constant and the sequence is simply taking multiples of that constant, there is nothing restricting the generation of perfect squares.

This is a very bold claim.
1. There is nothing apparent to you to restrict the generation of perfect squares as yet. That doesn't mean that there is a deeper reason why no solutions exist. For example, how many perfect squares are there in the Fibonacci sequence?
2. Note that in your example of getting another perfect square from $n = a \times 10^b$ , none of your seed values satisfy that condition (I'm assuming that $a$ and $b$ are integers. If not, please clarify further). Note further that since $C$ is irrational, $C \times n$ is not a finite decimal, and so $z$ is somewhat meaningless. (I'm guessing you wanted y to be an integer? If not, please clarify further)

Calvin Lin Staff - 3 years, 11 months ago

Using the square root of $2017$ is not restricting the result being a perfect square, therefore, among the infinite number of integers produced by the series, there must be an infinite amount of perfect squares

How do you know that there must be an infinite amount of perfect squares? Maybe there's only a finite amount of perfect squares? Maybe there isn't one at all?

Pi Han Goh - 3 years, 11 months ago

You can take any number in the infinite array number integers and multiply it by itself to get a perfect square, therefore, there is an infinite amount of perfect squares. And if you think about it, the square root of 2017 multiplied by an integer creates an infinite amount of numbers since you can multiple the square root with an infinite amount of numbers. Now, if you think about taking the floor function of a multiple of the square root of 2017, you will be making practically random integers, approximately $\sqrt{2017}$ away from each other. Now, this will create integers that can possibly be squared to equal another number in the series, and that process might even be able to be repeated (When I say possibly, I don't mean that I'm not sure if there is, but rather, there is an infinite number of solutions, therefore, I am not willing to test it out, however, I'm sure there is some way to prove it). So, there must be an infinite number of perfect squares in the series since both go on forever and mark practically random numbers.

Kevin Tong - 3 years, 11 months ago

Now, this will create integers that can possibly be squared to equal another number in the series, and that process might even be able to be repeated (When I say possibly, I don't mean that I'm not sure if there is, but rather, there is an infinite number of solutions, therefore, I am not willing to test it out, however, I'm sure there is some way to prove it).

You said "can possibly" and "might even be able to", so you're not sure of your own conviction either.

Pi Han Goh - 3 years, 11 months ago

Irrationally, Can This Happen?

3 solutions

Moderator note:

0 pending reports