Is it a Circle?

Calculus Level 5

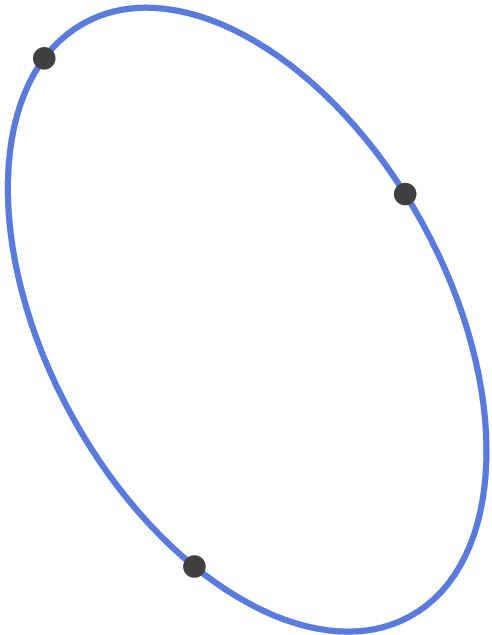
An ellipse passes through the points $(0,-1)$ , $(2,0)$ , and $(-2,2)$ and encloses minimum possible area.

$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$ is the equation representing the ellipse, where $A$ and $B$ are positive coprime integers.

Find $A+B+C+D+E+F$ .

The answer is -1.

4 solutions

David Vreken
Jul 8, 2019

Using $(0, -1)$ gives the equation $A(0)^2 + B(0)(-1) + C(-1)^2 + D(0) + E(-1) + F = 0$ which simplifies to:

$C - E + F = 0$

Similarly, using $(2, 0)$ and $(-2, 2)$ gives:

$4A + 2D + F = 0$

$4A - 4B + 4C - 2D + 2E + F = 0$

Replacing $x$ with $x + h$ and $y$ with $y + k$ gives the equation $Ax^2 + Bxy + Cy^2 + (2Ah + Bk + D)x + (Bh + 2Ck + E)y = -(Ah^2 + Bhk + Ck^2 + Dh + Ek + F)$ , which represents an equation of an ellipse centered at the origin, so that $2Ah + Bk + D = 0$ and $Bh + 2Ck + E = 0$ . The least area of any ellipse circumscribed about the triangle is the Steiner ellipse , and its center is the triangle's centroid, which in this case is $(h, k) = (\frac{0 + 2 + -2}{3}, \frac{-1 + 0 + 2}{3}) = (0, \frac{1}{3})$ . Therefore, $2A(0) + B(\frac{1}{3}) + D = 0$ and $B(0) + 2C(\frac{1}{3}) + E = 0$ , or:

$B + 3D = 0$

$2C + 3E = 0$

These five equations can be solved to $B = \frac{12}{7}A$ , $C = \frac{12}{7}A$ , $D = -\frac{4}{7}A$ , $E = -\frac{8}{7}A$ , and $F = -\frac{20}{7}A$ .

Choosing $A = 7$ will make $A$ and $B$ positive coprime integers, so that $B = 12$ , $C = 12$ , $D = -4$ , $E = -8$ , $F = -20$ , and $A + B + C + D + E + F = \boxed{-1}$ .

Mark Hennings
Jul 7, 2019

For three non-collinear vectors $\mathbf{a}$ , $\mathbf{b}$ , $\mathbf{c}$ , consider the affine transformation $T\mathbf{x} = A(\mathbf{x}-\mathbf{g})$ , where $\mathbf{g}=\tfrac13(\mathbf{a}+\mathbf{b}+\mathbf{c})$ , where $A$ is a nonsingular matrix such that $T\mathbf{a} \; = \; \binom{0}{2} \hspace{1cm} T\mathbf{b} \;=\; \binom{\sqrt{3}}{-1} \hspace{1cm} T\mathbf{c} \; = \; \binom{-\sqrt{3}}{-1}$ and, of course, $T\mathbf{g} = \mathbf{0}$ . Then it is easy to see that $T$ maps the ellipse $\mathcal{E}$ of least area that passes through the points with position vectors $\mathbf{a}$ , $\mathbf{b}$ , $\mathbf{c}$ to the ellipse of least area that passes through the points $\binom{0}{2}$ , $\binom{\sqrt{3}}{-1}$ , $\binom{-\sqrt{3}}{-1}$ , namely the circle $x^2 + y^2 = 4$ . Since this circle has parametric equation $\mathbf{x} \; = \; \binom{0}{2}\sin t + \tfrac{1}{\sqrt{3}}\left[\binom{\sqrt{3}}{-1} - \binom{-\sqrt{3}}{-1}\right]\cos t$ we deduce that the ellipse $\mathcal{E}$ has parametric equation $\mathbf{x} \; = \; \mathbf{g} + \big(\mathbf{a}-\mathbf{g}\big)\sin t + \tfrac{1}{\sqrt{3}}\big(\mathbf{b}-\mathbf{c}\big)\cos t$ In this case we have $\mathbf{a} = \binom{0}{-1} \hspace{1cm} \mathbf{b} = \binom{2}{0} \hspace{1cm} \mathbf{c} = \binom{-2}{2} \hspace{1cm} \mathbf{g} = \binom{0}{\frac13}$ and so the parametric equation of $\mathcal{E}$ is $\binom{x}{y} \; = \; \binom{0}{\frac13} + \binom{0}{-\frac43}\sin t + \tfrac{1}{\sqrt{3}}\binom{4}{-2}\cos t$ which leads to the Cartesian equation $7x^2 + 12xy + 12y^2 - 4x - 8y - 20 \; = \; 0$ for $\mathcal{E}$ . Thus the answer is $7+12+12-4-8-20 = \boxed{-1}$ .

Note that the ellipse $\mathcal{E}$ is the Steiner ellipse of the three points $(0,-1)$ , $(2,0)$ , $(-2,2)$ , being the unique ellipse through these three points whose centre is the centroid of the three points.

The equation and the answer are correct.
The Steiner ellipse was mentioned; but, no reference to the proof that the Steiner ellipse is, in fact, the minimal area eclipse through those points.
The computation that produces $\bm{T}$ was not even sketched.
Hosam Hajir's solution sketches the proof that the Steiner ellipse is the minimal area ellipse; but the final step was omitted: the proof that an equilateral triangle is the largest area triangle within a circle. But, that step is minor and can be done several ways.
The important point is that except for the final scaling transformations which have known effects on the triangle's area,all the rest of the transformations from the original triangle to a equilateral triangle of the same area with its base horizontal are affine transformations which are area preserving.
the transformations from a unit circle at the origin to the final ellipse are: a) an enlargement by a factor of $\sqrt{\frac{5}{3}}$ to brings the equilateral triangle so that the next transformation restores the original area, b) a scaling in the $y$ -axis direction by $\frac{16}{5 \sqrt{3}}$ to the original area, c) a shearing transformation slanting the $y$ axis leftward by an angle of $\tan ^{-1}\left(\frac{7}{16}\right)$ radians, d) a rotation transformation counter-clockwise by $\cot ^{-1}(2)$ , and e) a translation upwards by $\frac13$ . The unit circle is now the desired ellipse..
The conjugate semidiameters are the unit vectors along the positive $x$ and $y$ axes as transformed above. By using the Rytz's construction the semimajor and semiminor semiaxes can be derived. From there, a solution of multiple equations in multiple unknowns derives the ellipse's equation which then merely needs to be put into the problem's required form to compute the answer.

A Former Brilliant Member - 1 year, 11 months ago

The computation that produces $T$ is unnecessary --- it is enough that $T$ exists. Since any affine transformation provides an area scale factor of $|A|$ , where $A$ is the nonsingular matrix associated with $T$ , it is trivial that affine transformations map minimum area shapes to minimum area shapes, and the details of the transformations are unimportant - your points 3,5,6 are therefore irrelevant. It is possible to obtain a parametric equation for $\mathcal{E}$ that just depends on the three vertices $\mathbf{a}$ , $\mathbf{b}$ and $\mathbf{c}$ .

This current question is a (to my mind) unnecessary edited version of a previous problem. My proof of that result observed how to obtain the semimajor and semiminor axes by considering the eigenvalues of the symmetric matrix defining the ellipse: in this case $\left(\begin{array}{cc} 7 & 6 \\ 6 & 12 \end{array}\right)$ This version of the question did not ask for this information, so I did not bother. That answers point 7.

My comment that this was the Steiner ellipse was just that - a comment. However, this I have constructed $\mathcal{E}$ as the ellipse whose centre is the centroid of the points $\mathbf{a}$ , $\mathbf{b}$ and $\mathbf{c}$ , and that is the definition of the Steiner ellipse, I am not sure what you worried about in point 2.

Mark Hennings - 1 year, 11 months ago

Point 1 is intended as politeness towards you, to tell inform others that I was not contesting your final results.

Point 2 is at the heart of my comment. This problem on its surface is a search for an ellipse over huge parameter space to find the ellipse with the minimum area. Knowing that the Steiner ellipse with its centroid at the centroid of the triangle formed by the points is the path to the solution, which I believe is your final point above.

That fact has to be proved in the solution or by reference (preferably with a web link (I searched for, but was unable to find, such a proof)). That is exactly the purpose of points 4, 5 and 6, providing the proof for the problem's specific case. Those steps easily can be generalized to provide the general proof that the Steiner ellipse is the minimal area ellipse. It is evident from what I did find on the web that the proof was known and was derived from the fact that the centroids of an equilateral triangle and its circumcircle are the same and that that equilateral triangle is the maximal area triangle that can be enclosed within that circumcircle.

It is also evident that the Steiner inellipse has one-quarter of the area of the Steiner ellipse and the same aspect ratio as the Steiner ellipse.

In reference to point 3, I assumed, apparently falsely, the $\bm{T}$ was part of the derivation of the ellipse's equation.

Re point 7, would you, please, sketch the steps from the problem's data to the ellipse's equation, showing the nature of the computations?

See Steiner ellipse, minimal area through three points for the kind of solution for which I was hoping.

A Former Brilliant Member - 1 year, 11 months ago

Here we go. If $\mathcal{E}$ is the smallest area ellipse that circumscribes a given triangle, then (if $T$ is an affine transformation that maps the vertices of the triangle to the vertices of an equilateral triangle $\Delta$ centred on the origin, while mapping the centoid to the origin) $T(\mathbf{E})$ is the minimum area ellipse that circumscribes the equilateral triangle $\Delta$ .If $T(\mathcal{E})$ is not a circle, we can find a one-dimensional stretch that maps the ellipse $T(\mathcal{E})$ to a circle, and then $ST(\mathcal{E}))$ is the minimum area ellipse circumscribing $S(\Delta)$ , which which will not be equilateral. It is easy to see that $S(\Delta)$ would have to be the triangle of maximum area inside the circle $ST(\mathcal{E})$ , which would mean that $S(\Delta)$ was equilateral, which is not true. Thus we deduce that $T(\mathcal{E})$ is a circle. It is easy to write down a parametric equation for $\Delta$ , and from this apply $T^{-1}$ to obtain a parametric equation for $\mathcal{E}$ .

Referring to my proof, I chose a particular equilateral triangle, and obtained the equation $\binom{x}{y} \; =\; \binom{0}{\frac13} + \binom{0}{-\frac43}\sin t + \tfrac{1}{\sqrt{3}}\binom{4}{-2}\cos t$ for $\mathcal{E}$ . Thus $\cos t \; = \; \tfrac14\sqrt{3}x \hspace{2cm} \sin t \; =\; \tfrac34\big(\tfrac13 - \tfrac12x - y\big)$ Squaring and adding to eliminate $t$ gives the Cartesian equation for $\mathcal{E}$ .

Mark Hennings - 1 year, 11 months ago

Thank you.

A Former Brilliant Member - 1 year, 11 months ago

Could you please help me with something?

How do i find an ellipse through four given points that has the closest resemblence to a circle (the ellipse with minimum eccentricity)?

Digvijay Singh - 1 year, 10 months ago

Without trying too hard, here is an elementary method. The ellipse will have equation of the form $x^2 + 2Bxy + Cy^2 + Dx + Ey + F \; = \; 0$ where $C > B^2$ . Fitting this ellipse to the four points, we can find $B,C,D,E,F$ as functions of some single variable $t$ , say. You will doubtless have to restrict $t$ to some range to ensure that $C > B^2$ , so that we have an ellipse and not some other conic.

The semi-major and semi-minor axes of the ellipse are $\tfrac{1}{\sqrt{\lambda}}$ and $\tfrac{1}{\sqrt{\mu}}$ where $0 < \lambda < \mu$ are the eigenvalues of the matrix $\left(\begin{array}{cc} 1 & B \\ B & C\end{array}\right)$ . Thus the eccentricity of the ellipse is $e$ , where $e^2 \; =\ ; 1 - \tfrac{b^2}{a^2} \; = \; 1 - \tfrac{\lambda^2}{\mu^2}$ Since $\lambda,\mu$ are known functions of $t$ , so is $e$ . Standard calculus (or, failing that, some numerical work) should enable you to find the value of $t$ that minimizes $e$ .

Mark Hennings - 1 year, 10 months ago

I did it this way, could you tell me if its correct?

Let $L_1,L_2,L_3,L_4$ be the four lines pairwise passing through the four points.

Then the equation of the conics through the four points will be $L_1 L_2+\lambda L_3 L_4=0$

Now we have the family of conics passing through the four points and determined by the parameter $\lambda$ .

How do I find an expression for $e$ using this general equation of the conics?

Digvijay Singh - 1 year, 10 months ago

@Digvijay Singh – So if $L_1,L_2,L_3,L_4$ are four lines passing through $p$ & $q$ , $r$ & $s$ , $p$ & $r$ and $q$ and $s$ respectively, and if the four equations are $a_jx + b_jy + c_j \; = \; 0 \hspace{2cm} 1 \le j\ le 4$ then the equation $(a_1x + b_1y + c_1)(a_2x + b_2y + c_2) + \lambda(a_3x + b_3y + c_3)(a_4x + b_4y + c_4) \; = \; 0$ will be a conic passing through $p,q,r,s$ for any $\lambda$ . We now expand to get $(a_1a_2 + \lambda a_3a_4)x^2 + (a_1b_2 + a_2b_1 + \lambda a_3b_4 + \lambda a_4b_3)xy + (b_1b_2 + \lambda b_3b_4)y^2 + \cdots \; = \; 0$ and so we are back to analysing the matrix $\left( \begin{array}{cc} a_1a_2 + \lambda a_3a_4 & \tfrac12(a_1b_2 + a_2b_1 + \lambda a_3b_4 + \lambda a_4b_3) \\ \tfrac12(a_1b_2 + a_2b_1 + \lambda a_3b_4 + \lambda a_4b_3) & b_1b_2 + \lambda b_3b_4\end{array}\right)$ to determine the eigenvalues, and hence the semimajor and semiminor axes of the ellipse.

Mark Hennings - 1 year, 10 months ago

Hosam Hajjir
Jul 8, 2019

Let the given points be $\mathbf{a} = (0, -1) , \mathbf{b} = (2, 0) , \mathbf{c} = (-2,2)$ . We're going to transform the given set of points into another set that are the vertices of an unit equilateral triangle, with the following vertices: $\mathbf{a'} =(0, 0), \mathbf{b'}=(1, 0), \mathbf{c'} = ( \dfrac{1}{2}, \dfrac{\sqrt{3}}{2} )$ . So we define our linear transformation as follows

$\mathbf{y} = L(\mathbf{x}) = A (\mathbf{x} - \mathbf{a} )$

For a $2 \times 2$ matrix $A$ . With this definition, the image of point $\mathbf{a}$ is automatically the point $\mathbf{a'}$ , so what remains it to plug in the two other points, so that we have the following matrix equation:

$[ \mathbf{b'} , \mathbf{c'} ] = A [ \mathbf{b}-\mathbf{a} , \mathbf{c} - \mathbf{a} ]$

It follows that $A = [ \mathbf{b'} , \mathbf{c'} ] [ \mathbf{b}-\mathbf{a} , \mathbf{c} - \mathbf{a} ]^{-1}$

Now the minimum area ellipse passing through $\mathbf{a} , \mathbf{b}, \mathbf{c}$ corresponds to the minimum area ellipse passing through $\mathbf{a'} , \mathbf{b'}, \mathbf{c'}$ , which is the circumcircle of the unit equilateral triangle, $\triangle \mathbf{a'} \mathbf{b'} \mathbf{c'}$ , that is a circle of radius $\dfrac{1}{\sqrt{3}}$ , and centered at $\mathbf{y_0} = (\dfrac{1}{2}, \dfrac{\sqrt{3}}{6} )$ . The equation of this circle is therefore,

$(\mathbf{y} - \mathbf{y}_0 )^T (\mathbf{y} - \mathbf{y}_0 ) = \dfrac{1}{3}$

but $\mathbf{y} = A (\mathbf{x} - \mathbf{a} )$ , therefore,

$(A (\mathbf{x} - \mathbf{a} ) - \mathbf{y}_0 )^T (A (\mathbf{x} - \mathbf{a} ) - \mathbf{y}_0 ) = \dfrac{1}{3}$

And this becomes after re-arranging,

$( \mathbf{x} - \mathbf{a} - A^{-1} \mathbf{y}_0 )^T A^T A ( \mathbf{x} - \mathbf{a} - A^{-1} \mathbf{y}_0 ) = \dfrac{1}{3}$

In final form this becomes

$( \mathbf{x} - \mathbf{x}_0 )^T Q ( \mathbf{x} - \mathbf{x}_0 ) = 1$

where $\mathbf{x}_0 = \mathbf{a}+ A^{-1} \mathbf{y}_0$ and $Q = 3 A^T A$ .

Expanding this quadratic form gives the desired general equation of a conic.

K T
Jul 20, 2019

UNDER CONSTRUCTION - I am working on presenting the solution, it follows shortly....

Is it a Circle?

The answer is -1.

4 solutions

1 pending report

Vote up reports you agree with