Is it a perfect blend of Mechanics and Calculus?
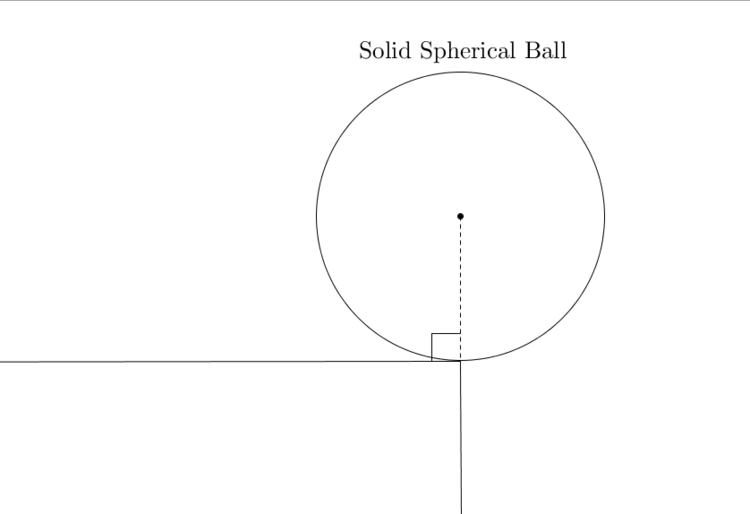 A solid spherical ball is placed carefully on the edge of a table in the position shown in the figure. The coefficient of static friction and kinetic friction between the ball and the edge of the table is 0.5 . It is then given a very slight push. It begins to fall off the table.
A solid spherical ball is placed carefully on the edge of a table in the position shown in the figure. The coefficient of static friction and kinetic friction between the ball and the edge of the table is 0.5 . It is then given a very slight push. It begins to fall off the table.
Find the angle (in degrees) turned by the ball before it looses contact with the edge.
Details and Assumptions :
1) Find the angle with the vertical.
2) Before solving this try this .
3) You may use WolframAlpha if you want.
Image credit---Pratik's Ball don't fall. .
The answer is 52.71.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I have already asked you all in the question to try this before attempting this question.
So here I am not writing the equations which can be found by using FBD's and energy conservation. But I am uploading FBD's which are quite helpful.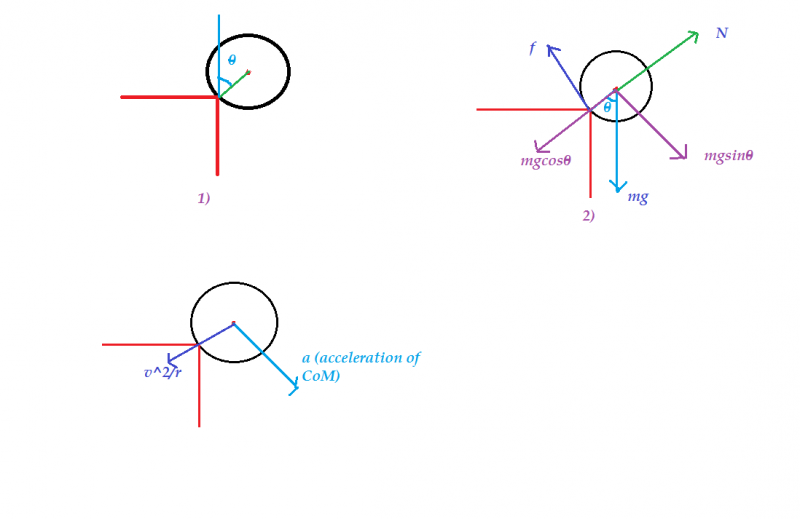
Let θ be the angle with the vertical at which the ball is slipping and rotating together. But the CoM of the sphere still performs circular motion about the edge. Let the tangential velocity and the acceleration of the CoM at that particular angle θ be v and a respectively. Let ω be the angular velocity of the CoM of the ball about the edge.
So I have 2 equations-
m g c o s θ − N = m r v 2 .............(1)
and m g s i n θ − μ N = m a
From eq(1) m g c o s θ − m r v 2 = N
or and m g s i n θ − μ ( m g c o s θ − m r v 2 ) = m a
So m g s i n θ − μ ( m g c o s θ − m r v 2 ) = m d t d v
or m g s i n θ − μ ( m g c o s θ − m r v 2 ) = m d θ d v ω
But ω = r v
NOTE--Here v is the tangential velocity of the CoM at angle θ and ω is the angular velocity of the CoM of the ball about the edge and the ball is doing circular motion about the edge. So we can use this equation v = r ω
So m g s i n θ − μ ( m g c o s θ − m r v 2 ) = m r d θ v d v
Let v 2 = x So 2 v d v = d x
So g s i n θ − μ ( g c o s θ − r x ) = 2 r d θ d x
2 r d θ d x = g s i n θ − μ g c o s θ + μ r x
d θ d x − 2 μ x + 2 r g ( μ c o s θ − s i n θ ) = 0
Here I F = e ∫ − d θ = e − θ
x e − θ = ∫ e − θ { 2 r g ( s i n θ − μ c o s θ ) } d θ
x e − θ = 2 r g ∫ e − θ { ( s i n θ − μ c o s θ ) } d θ
x e − θ = 2 r g ∫ e − θ { ( s i n θ − μ c o s θ ) } d θ
x e − θ = 2 r g ∫ e − θ s i n θ d θ − μ ∫ e − θ c o s θ d θ
x e − θ = 2 r g { − 2 e − θ ( s i n θ + c o s θ ) − 2 1 2 e − θ ( s i n θ − c o s θ ) }
x e − θ = − r g e − θ { 1 ( s i n θ + c o s θ ) + 2 ( s i n θ − c o s θ ) }
x e − θ = − r g e − θ { 2 3 s i n θ + c o s θ } + C
x = − r g { 2 3 s i n θ + c o s θ } + C e θ
We can find the value of C by finding x at angle 43.82 deg.
So
1 0 r 7 v 2 = g ( 1 − c o s θ ) I got this from equation energy conservation-
Putting g=9.8 θ = 4 1 . 8 2 I got v 2 = 3 . 5 6 r
Now the the solution differential equation was
x = − r g { 2 3 s i n θ + c o s θ } + C e θ .
where x = v 2
So at θ = 4 1 . 8 2 v 2 is 3 . 5 6 r
So putting values I got
3 . 5 6 r = − r g { 2 3 s i n ( 4 1 . 8 2 ) + c o s ( 4 1 . 8 2 ) } + 2 . 7 2 0 . 7 3 C
So the value of C = 8 . 2 0 r
So v 2 = − r g ( 2 ( 3 s i n θ + c o s θ ) ) + 8 . 2 0 r e θ
or r v 2 = − g ( 2 ( 3 s i n θ + c o s θ ) ) + 8 . 2 0 e θ
but r v 2 = g c o s θ (got this relation from the equation for the moment at which ball looses contact with the cliff)
or g c o s θ = − g ( 2 ( 3 s i n θ + c o s θ ) ) + 8 . 2 0 e θ
Now according to WolframAlpha the answer is 5 2 . 7 1 .