Is it geometry II?

First of all,we see a striking resemblance between the three equations and the cosine law as there are three square values and tow of them have been multiplied. $$ The cosine law is $c^2=a^2+b^2-2ab\cos\theta$ ,where $\theta$ is the angle opposite to the side $c$ .Now if we compare the law and the first equation we get that $c=5,x=a,y=b$ and $-2xy\times \cos\theta=1$ hence $\cos\theta$ should be $\dfrac{-1}{2}$ which means $\theta=120^{\circ}$ .Comparing the other two equations also we get three triangles Now,seeing that all three triangles have one angle equal to $120^{\circ}$ ,we think that they can be joined at one common vertex,doing so we get a triangle with sides, $(5,12,13)$ which is a right-angled triangle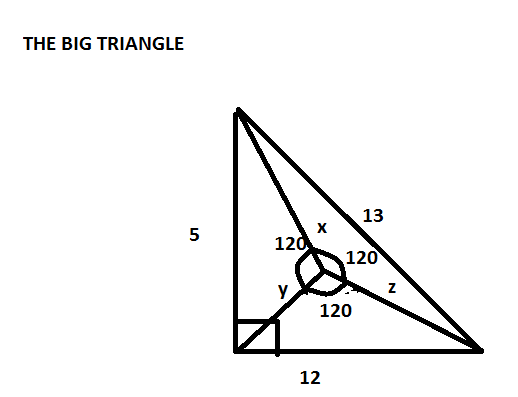

Now,the area of the big triangle would be $30 \text{unit}^2$ which is equal to the sum of the areas of the three small triangles.Hence,we have from the sine rule that, $30=\dfrac{1}{2} \times \sin120^{\circ}(xy+yz+zx)$ .From here we can easily find the answer. $$ In response to the Challenge Master's Note: $$ Yes,sir the condition"positive" is needed as we have taken them to be sides of the triangle. Cheers!