How Is It Going To Move?
A thin uniform rod of A B (of length ℓ ) is sliding, keeping in touch with a vertical smooth surface and a horizontal smooth surface as shown in the figure below.
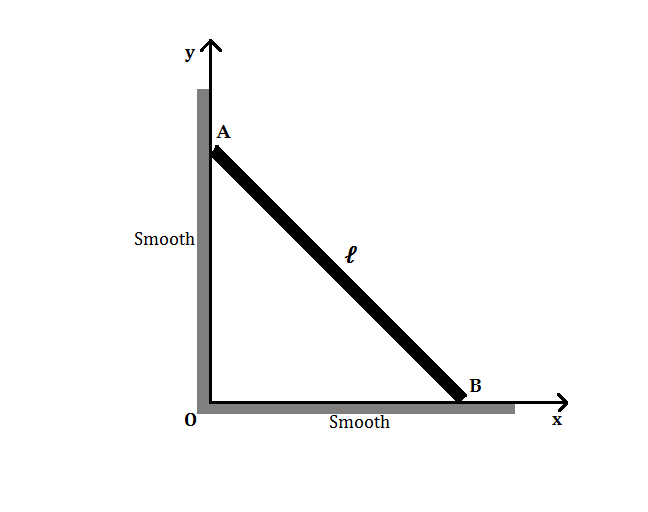
Taken any point on the rod, which of the following are the possible loci of its path?
If you liked this problem, why don't you try another one ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
From where did you manage to get the image ?
Log in to reply
Get the image? I designed it on MS Paint.
Log in to reply
great work .
My questions: (1) Will it ever leave contact with the vertical wall , if yes, then at which angle?
(2) What can be said about its motion after its vertical height becomes zero ?
(3) Where can I get more problems and analysis over this case?
@Tapas Mazumdar ; @Chew-Seong Cheong sir please help...
Let a point P on the rod A B be a from A and b from B . That is a + b = ℓ . Then the coordinates of P ( x , y ) (from the origin O ), when the rod is inclined at ∠ A B O = θ are given by:
⎩ ⎨ ⎧ a x = cos θ b y = sin θ ⟹ a 2 x 2 + b 2 y 2 = cos 2 θ + sin 2 θ = 1
a 2 x 2 + b 2 y 2 = 1 is the equation of a ellipse. When a = b , the equation is a circle. We note that x = a cos θ and y = b sin θ . When a = 0 , we get P ( 0 , b sin θ ) , which is a vertical straight line, and when b = 0 , we get P ( a cos θ , 0 ) , a horizontal straight line.
Therefore, the answer is Straight line, Circle, Ellipse .
Less elaborative but directly on point. :)
Elegant and simple as always..sir.
There are only three possible paths on which a point on the rod can move:
Consider the two end points A and B of the rod.
At any given instant we can observe that the point A moves vertically downward on the y - axis and the point B moves horizontally on the x - axis . Hence, the locus of path of A and B are the straight lines x = 0 and y = 0 respectively.
Consider the coordinates of center of mass be ( x , y ) .
From the frame of the rod (which is uniform), it is clear that its center of mass will lie exactly in the middle. Hence, the point ( x , y ) is at a distance of 2 ℓ from either end of the rod. Let us take the angle of inclination of rod from the horizontal surface be θ . Take components 2 ℓ cos θ and 2 ℓ sin θ of the length vector 2 ℓ on the x - axis and y - axis respectively. From this, we conclude that,
x y = = 2 ℓ cos θ 2 ℓ sin θ
Eliminating θ gives,
x 2 + y 2 ⟹ 4 x 2 + 4 y 2 = = 4 ℓ 2 ℓ 2
Which is the equation of a circle.
Consider any other variable point ( x , y ) on the rod situated at a distance a from the end A of the rod and b from the end B of the rod. Again take the angle of inclination as θ and take component a cos θ of length vector a along the x - axis and component b sin θ of length vector b along the y - axis . From here, we conclude that,
x y = = a cos θ b sin θ
Eliminating θ gives,
a 2 x 2 + b 2 y 2 = 1
Which is the equation of an ellipse.
Important Note: We have not considered the situation when the rod losses contact with the vertical surface and starts slipping on the horizontal surface as after this moment, all points on the rod will have the same path, i.e., a straight line y = 0 .