Is it small enough?
Given two non-overlapping circles of radii 4 and 5 , what is the smallest equilateral triangle which can contain them?
If the side of such a triangle is a b + c d , where a , b , c , and d are integers with b and d being square-free, submit a + b + c + d .
The answer is 21.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Thank you for putting in the effort to prove the optimal orientation. I had wondered about this, but used my "proof by intuition :)" to quiet my mind. Nice, effective animation. Now let's try three circles ...
The smallest equilateral triangle to contain the two circles would be one that is tangent to the circles when the two circles are tangent to each other:

That means A E bisects ∠ D A H so that ∠ E A H = 2 1 ∠ D A H = 2 1 6 0 ° = 3 0 ° and A B = tan 3 0 ° 4 = 4 3 , and D G bisects ∠ A D H so that ∠ G D C = 2 1 ∠ A D H = 2 1 6 0 ° = 3 0 ° and C D = tan 3 0 ° 5 = 5 3 .
By the Pythagorean Theorem on △ E F G , E F = E G 2 − F G 2 = 9 2 − 1 2 = 4 5 .
Therefore, the side of the equilateral triangle is A D = A B + B C + C D = 4 3 + 4 5 + 5 3 = 9 3 + 4 5 , which means a = 9 , b = 3 , c = 4 , d = 5 , and a + b + c + d = 2 1 .
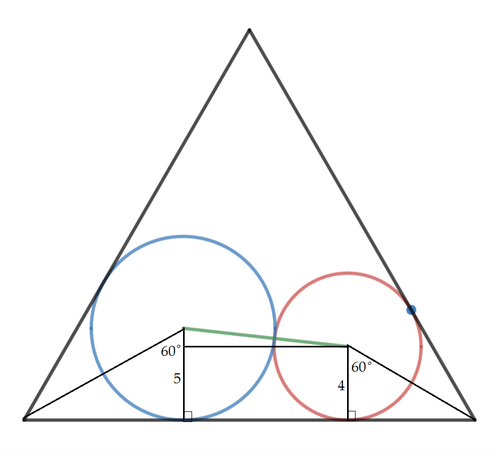
The smallest circumscribing equilateral triangle is one with both circles tangent to onw of its sides (see proof below). Then the side of this smallest equilateral triangle is a = 5 tan 6 0 ∘ + 9 2 − 1 2 + 4 tan 6 0 ∘ = 9 3 + 4 5 . Therefore a + b + c + d = 9 + 3 + 4 + 5 = 2 1 .
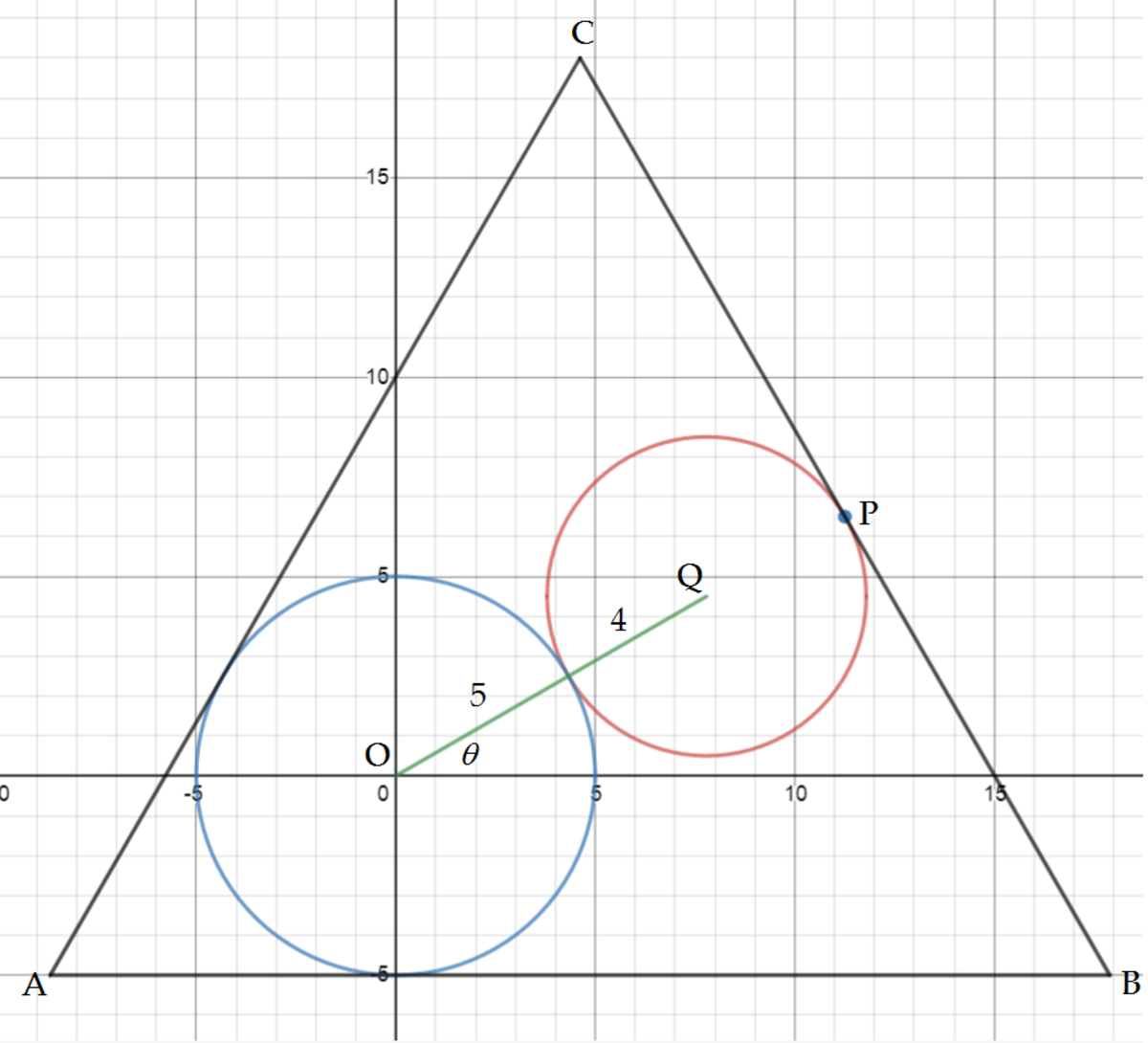
Proof: Fix the center of the circle with radius 5 at the origin O ( 0 , 0 ) , a vertex of the triangle at A ( − 5 3 , − 5 ) such that a triangle side tangent to the circle A B is along y = − 5 and the other side C A is at 6 0 ∘ to A B . Let the line joining the two centers O Q makes an angle θ with the x -axis. Then the equation of the circle with radius 4 is ( x − 9 cos θ ) 2 + ( y − 9 sin θ ) 2 = 4 2 … ( 1 ) . And the gradient at a point on the circle is given by 2 ( x − 9 cos θ ) + 2 ( y − 9 sin θ ) = 0 . Let the third side B C be tangent to the circle at P ( x 1 , y 1 ) . Then the gradient at P is − 3 and we have:
x 1 − 9 cos θ − 3 ( y 1 − 9 sin θ ) ⟹ x 1 − 9 cos θ 4 ( y 1 − 9 sin θ ) 2 ⟹ y 1 x 1 = 0 = 3 ( y 1 − 9 sin θ ) = 1 6 = 2 + 9 sin θ = 2 3 + 9 cos θ Substitute in (1)
Then the equation of B C is given by x − x 1 y − y 1 = − 3 . Let B ( x 2 , − 5 ) , then we have:
x 2 − x 1 − 5 − y 1 5 + y 1 ⟹ x 2 = − 3 = 3 x 2 − 3 x 1 = 3 5 + 3 x 1 + y 1 = 3 1 3 + 9 3 cos θ + 9 sin θ = 3 1 3 + 1 8 sin ( θ + 6 0 ∘ )
Since the side length a = B C = x 2 + 5 3 , a is minimum, when x 2 is minimum or sin ( θ + 6 0 ∘ ) or θ is minimum. The smallest θ = − sin − 1 9 1 . Then
a min = 3 1 3 + 1 8 ( − 9 1 ⋅ 2 1 + 9 8 0 ⋅ 2 3 ) + 5 3 = 9 3 + 4 5
4 3 + ( 5 + 4 ) 2 − ( 5 − 4 ) 2 + 5 3 = 9 3 + 4 5
Can you explain how you formed this expression?
Log in to reply
And also how you know for certain it's the minimum.
Log in to reply
when one circle tangent a angle and the other circle tangent the opposite line at the middle, it's easy to know the triangle is bigger.
when two circles tangent one side of triangle, the length at two ends are 4 3 and 5 3 respectively , and the middle part is ( 5 + 4 ) 2 − ( 5 − 4 ) 2
Log in to reply
You might want to include that in your solution. But still, how do you know it's the minimum?
Log in to reply
@Chris Lewis – fix one circle tangenting one angle, move the other circle around the fixed one in the triangle,then watch the smallest altitude
Even if you got the right configuration, how do you know that this produces the smallest equilateral triangle?
The equilateral triangle that contains the two circles also contains the smallest (in area) convex shape that encloses them. In order to minimise this shape, the circles have to be tangent to each other.
Next, we prove that the smallest equilateral triangle that contains the two circles is the one that has a side tangent to both circles and each circle is tangent to two sides of the triangle (as can be seen in the animation below).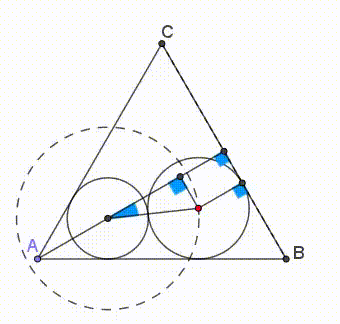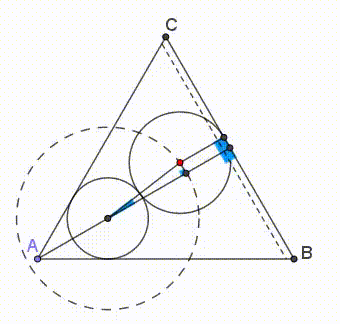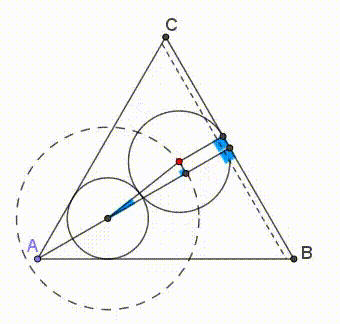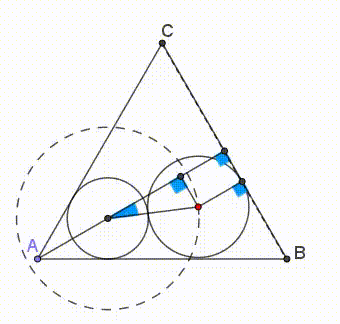
Proof
First we put one circle (e.g. the small one, but the argument is irrelevant to this choice) tangent to sides A B and A C . Then its center D lies on the angle bisector and altitude A F of △ A B C .
Obviously, the second circle must be tangent to side B C . Then, the smallest equilateral triangle occurs when A F is minimised.
Let ∠ G D E = θ , G E ⊥ A F , D K ⊥ A B and G H ⊥ B C , where G is the center of the second circle (figure 1).
Then,
A F = A D + D E + E F = D K ⋅ csc 3 0 ∘ + D G ⋅ cos θ + G H = 4 ⋅ 2 + 9 ⋅ cos θ + 5 = 1 3 + 9 ⋅ cos θ Hence, A F gets minimised when the acute angle θ takes its maximum value, which evidently happens when the second circle is tangent either to side A B , or side A C . Q.E.D.
Let G L ⊥ A B and D I ⊥ G L (figure 2)
By Pythagoras’ theorem on △ D G I , D I = D G 2 − G I 2 = D G 2 − ( G L − I L ) 2 = ( 4 + 5 ) 2 − ( 5 − 4 ) 2 = 4 5 Consequently,
A B = A K + K L + L B = D K ⋅ cot 3 0 ∘ + D I + G L ⋅ cot 3 0 ∘ = 4 3 + 4 5 + 5 3 = 9 3 + 4 5 For the answer, a = 9 , b = 3 , c = 4 , d = 5 , (or a = 4 , b = 5 , c = 9 , d = 3 ). In any case, a + b + c + d = 2 1 .