Half A Hypotenuse

Any right angle triangle is half of a rectangle.

The hypotenuse is a diagonal of the rectangle and both diagonals have equal length. Also, they bisect each other.

Hence the median is always half of the diagonal of the rectangle, or half of the hypotenuse.

Let $a,b$ be the sides of the right triangle and $c$ be the hypotenuse.

One can easily derive the formula of a median in a triangle with sides $x,y$ and $z$ and the median is drawn to side $x$ is $M_{x}=\frac{\sqrt{2y^2+2z^2-x^2}}{2}$ by Pythagoras theorem.

In our right triangle, $a^2+b^2= c^2$ and median is drawn to side $c$ .

$\begin{aligned} M_{c} & =\frac{\sqrt{2a^2+2b^2-c^2}}{2} \\ & = \frac{\sqrt{2c^2-c^2}}{2} \\ & =\frac{c}{2} \end{aligned}$

So, the answer is True.

I did it using mid point theorem

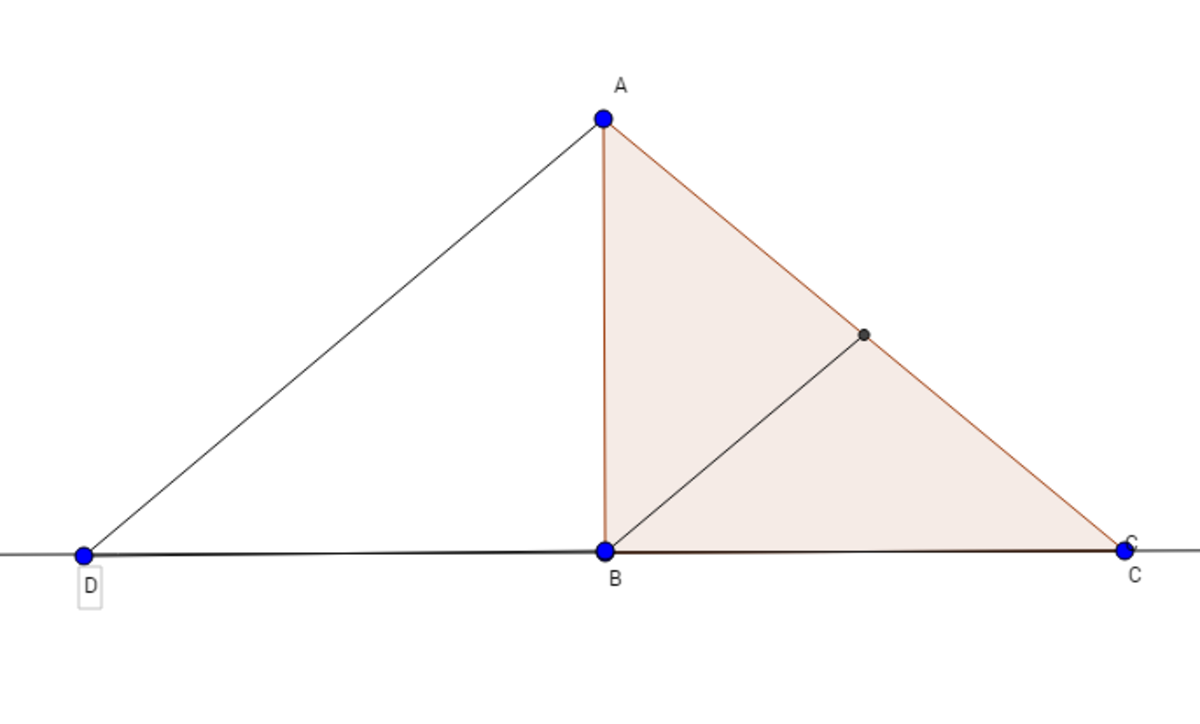
First thing extend BC to D such that BD=BC.

Now note triangle ADB and ABC are congurent so, AD=AC. Now in triangle ADC, B is the mid-point of CD and Let's say X is the mid-point of AC. Note that $BX=\dfrac{1}{2}AD=\dfrac{1}{2}AC$ which proves the statement of the question.

You can just inscribe the right triangle in a circle. The midpoint of the hypotenuse is the center of the circle. So, the diameter is 2r and the median is r.

consider DC as the diameter of a circle. DAC is right angle so it is on the perimeter of the some circle. So AB equals radius of the circle the same as DB and BC.

median line to the hypotenuse is equal to 1/2 of that edge

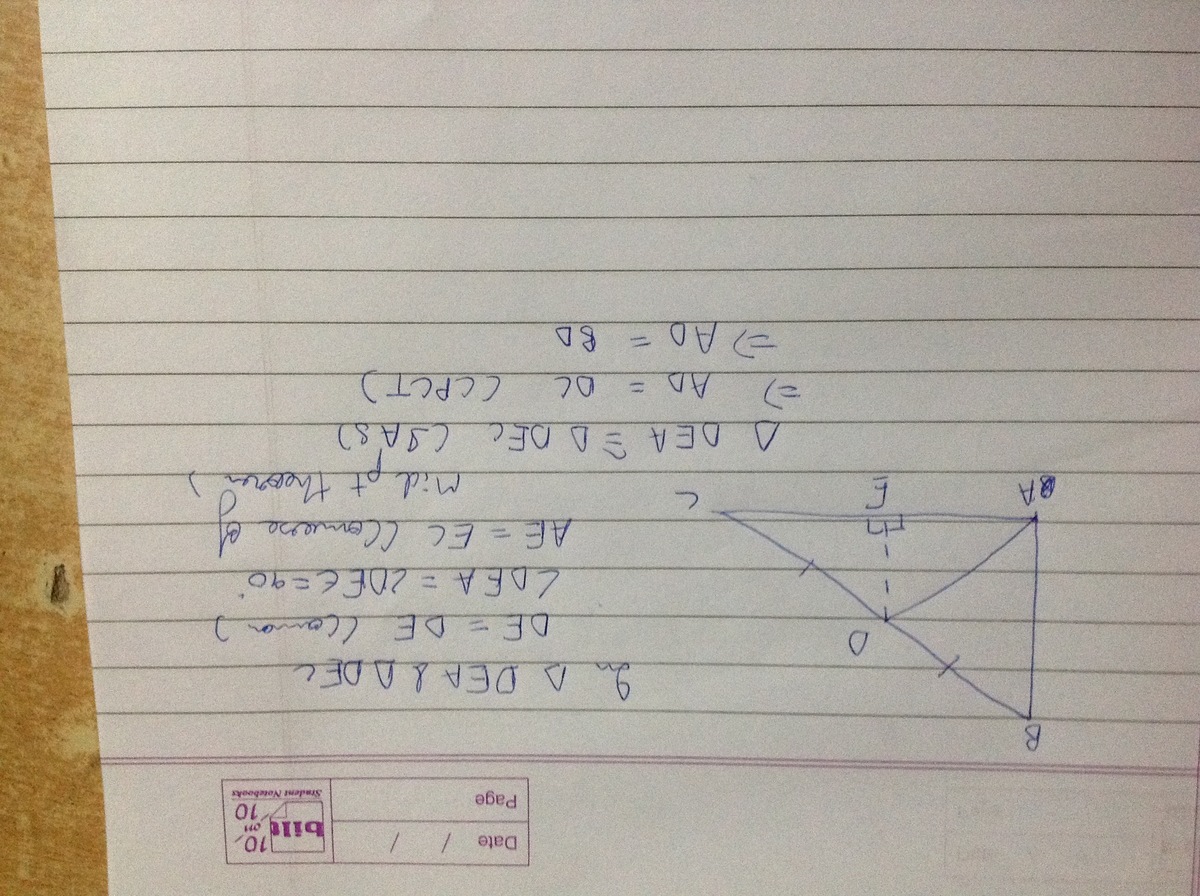
We have to make a construction by making a perpendicular from D to AC meeting at E. Now as angle BAC = angle DEA = 90 degree. BA is parallel to DE. With the help of converse of mid point theorem AE = EC. We can tell AD = AC. It is explained in the image below.