Is It Uniform Acceleration?
Assume that Earth is a perfect sphere with radius R . The time T an object takes to fall to the ground from rest from a height of R above the ground is given by T = g R ( A + C π B ) , where A , B , C are positive integers.
Find A + B + C .
Note: Consider only gravity, and forget about atmospheric effects, air resistance, etc.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Similar to your problem Symmetrical Sliding . Thank you for the awesome solution!
@Steven Chase, please tell where am i wrong?
At a height h above the earth's surface we have acceleration due to gravity as
g ′ = ( 1 + R h ) 2 g .
At that height only one force is acting on the mass, IE weight downward. So,
F net = m g ′ = ( 1 + R h ) 2 m g .
m d h v d v = ( 1 + R h ) 2 m g ⇒ v d v = ( 1 + R h ) 2 g d h ⇒ ∫ 0 v v d v = ∫ R 0 ( 1 + R h ) 2 g d h ⇒ 2 v 2 = 2 g ⇒ v = g .
Again,
v = d t d h = g ⇒ ∫ R 0 d h = ∫ 0 T g d t ⇒ T = g R .
Also, please help me in this one by me
https://brilliant.org/problems/infinitely-many-inclined-planes/?ref_id=1496573
Log in to reply
Hello. I agree with your g prime and F net expressions. What are you doing in the line after that? You would equate the force to -m * h(double dot) right?
Log in to reply
@Steven Chase , thanks for helping on that problem.
Please help me here more.
m d t 2 d 2 h = ( 1 + R h ) 2 m g ⇒ d t 2 d 2 h = g ( 1 − R 2 h ) .
Now how to show that
d t 2 d 2 h ∝ h
?
How to approximate now??
Log in to reply
@Priyanshu Mishra – There should be a negative sign on one side as well. And then the differential equation corresponds to simple harmonic motion. Of course, the equation is only valid until the object reaches the surface. You can apply initial conditions to determine the coefficients.
Regarding the other problem, the steps I followed were:
1) Determine the starting and ending locations of the center of mass. Be mindful of the fact that the center of mass is never actually on the parabola. For the initial condition, this requires a bit of geometry.
2) From the starting and ending COM locations, determine the change in potential energy.
3) Equate the change in potential energy to the sum of the translational and rotational kinetic energies.
4) Solve for omega and v. These two quantities are directly proportional by the disk radius.
Priyanshu mishra By that way you found velocity on reaching earth surface . You should find velocity as a function of height 'h'. So your limits for dh integral are from R to h.
I used mgh for calculating the GPE, but instead of one plus pi over two, I got root two. Why?
Log in to reply
Gravity decreases with altitude as one rises above the Earth's surface because greater altitude means greater distance from the Earth's centre.
The simple acceleration formula s = 0.5 * a * t^2 does not hold in this case, as the acceleration a (the gravity constant g) is not contstant. With the „simple“ formula, it would take the object 1.414 * sqrt(R/g), but as the acceleration grows over time upto g on the surface, it takes the object longer 2.571 * sqrt(R/g)
Could you please give a hint about how that integral is solved?
Log in to reply
I used an integral table
You can make the substitution r = 2 R sin 2 θ .
Would it be possible to solve it by considering the differential equation d t 2 d 2 x + x 2 G M = 0 ?
Log in to reply
Yes, that differential equation is correct.
Log in to reply
@Steven Chase , the force on mass m is always directed towards centre of earth , so why its motion will be SHM?
when we displace it upwards , it is attracted towards earth. when we displace downwards it is again attracted downwards.
Log in to reply
@Priyanshu Mishra – Imagine that there was a small hole in the earth through which it could pass. Then it's easy to see that it would be SHM. In our case, the SHM behavior only holds until the object hits the surface, and then the motion stops.
I guessed because I was confused I'm only in 7th grade.
It's all good. I'm only in my senior college year working on an engineering degree and I was confused. I think the question needs to clarify that it wants us to use known physics relationships rather than particular known constants or through a reworking of the equation's given variables.
I didn't get this one either...
To solve this problem
without using calculus
we will analyze the trajectory and keep in mind the Second Law of Kepler.
As we now, ever trajectory can be understood as a conic section, including this one. This path is a
degenerated ellipse
with focus on Earth center and apogee at the initial position, i.e. 2a = 2R.
Using the
Second Law of Kepler
, the flight time must be proportional to the area;
P
T
=
S
t
o
t
a
l
S
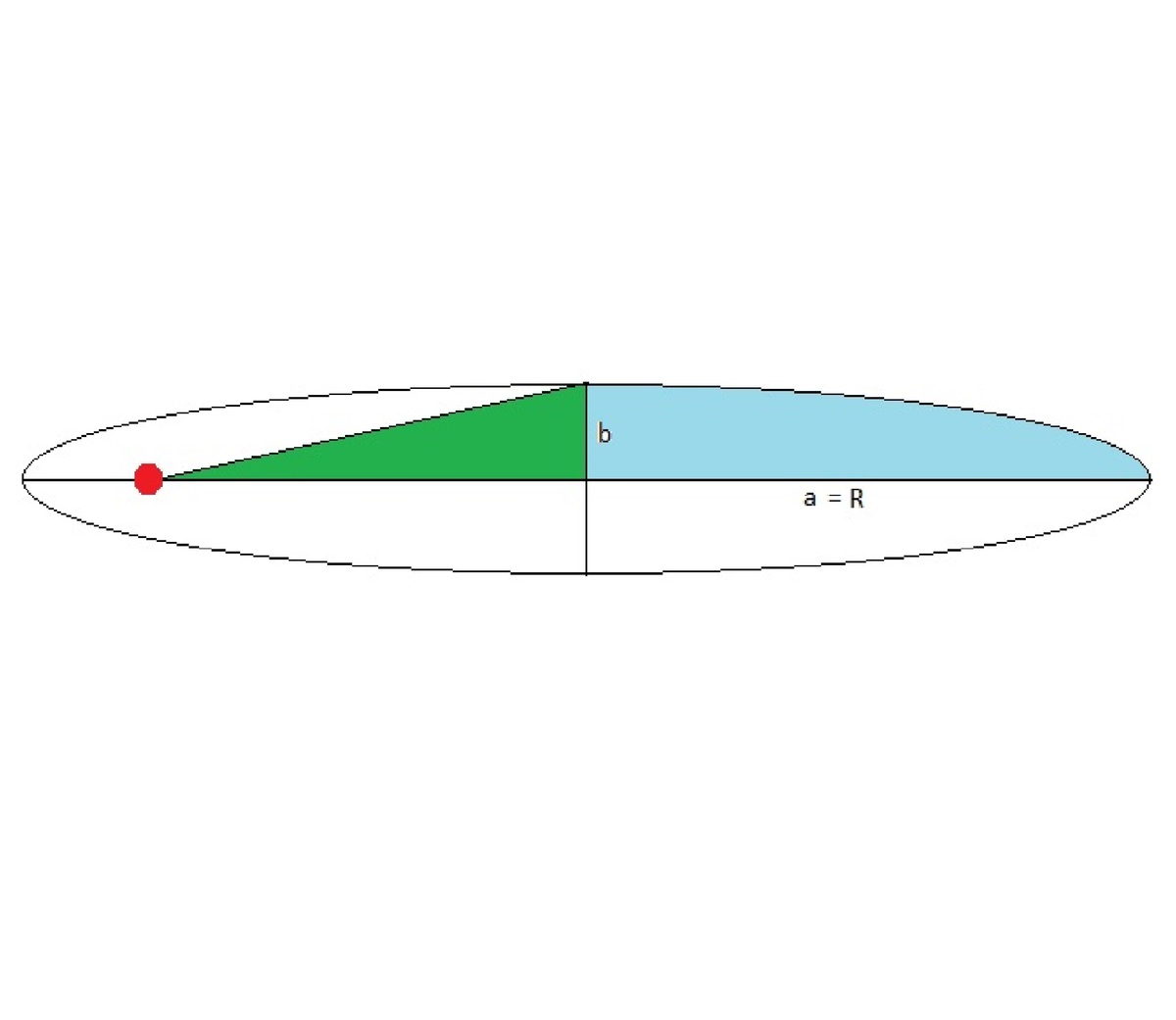 S
=
S
g
r
e
e
n
+
S
b
l
u
e
=
2
b
∗
a
2
−
b
2
+
4
P
i
∗
a
∗
b
When:
b
→
0
, which is the case:
S
=
S
g
r
e
e
n
+
S
b
l
u
e
=
2
b
∗
a
2
−
b
2
+
4
P
i
∗
a
∗
b
When:
b
→
0
, which is the case:
S
t
o
t
a
l
S
=
4
1
+
2
∗
P
i
1
And using from classical mechanics that P = 2 Pi
g
R
and from geometry S t o t a l = P i ∗ a ∗ b , we have that:
T = P * S t o t a l S = g R * ( 1 + 2 P i )
So A=B=1 and C=2.
Thank you for the wonderful solution! By the way, P = 2 π g R can be computed by the Third Law of Kepler .
I stared at this the way a dog might stare at a Rubik's Cube, and with all seriousness typed in "4". Then I hit enter and get told it's correct, and I now believe I am a secret genius.
Let r be the distance from the Earth's center. Equate the change in potential energy to the kinetic energy:
G M m ( r 1 − r 0 1 ) = 2 1 m ( d t d r ) 2
Re-arranging gives:
d t = − 2 G M 1 r 1 − r 0 1 1 d r = − 2 G M r 0 r 0 − r r d r
Total ellapsed time:
T = − 2 G M r 0 ∫ r 0 R r 0 − r r d r = G M R ∫ R 2 R 2 R − r r d r = G M R ( 1 + 2 π ) R = G M R 3 ( 1 + 2 π )
Earth mass in terms of Earth surface gravity:
R 2 G M m = m g M = G g R 2
Plugging in:
T = G M R 3 ( 1 + 2 π ) = G G g R 2 R 3 ( 1 + 2 π ) = g R ( 1 + 2 π )