This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Or you can just complete the square: x 2 + 8 x + 1 = ( x + 4 ) 2 − 1 5 → x → ∞ ( x + 4 ) 2 = x + 4 .
Log in to reply
Maybe. See, I'm a tenth standard student. Calculus is not in our syllabus. It is in our next class. I just found calculus interesting so I started it. I gave this question because it was quite interesting. But see, I haven't yet gone too much into calculus yet. So I can't understand your completing square method. I've come across this 'completing square' system in quadratic equations. But I couldn't relate it to calculus. But thanks, :) I will look forward to it in class 11.
Log in to reply
Okay, think of it this way:
We know that x 2 + 8 x + 1 = x 2 + 8 x + 1 6 − 1 5 = ( x + 4 ) 2 − 1 5 . When x becomes super duper large (in other words, as x tends to infinity), ( x + 4 ) 2 becomes super duper ultra awesome large right? And that super duper ultra awesome large minus a small number of 15 is still a super duper ultra awesome large number right? So we say that for x becomes unboundedly large, ( x + 4 ) 2 − 1 5 ≈ ( x + 4 ) 2 .
Now, back to the question, we want to evaluate the limit as x becomes unboundedly large in the positive direction (in other words, as x tends to ∞ ), then x 2 + 8 x + 1 = ( x + 4 ) 2 − 1 5 is approximately equals to ( x + 4 ) 2 right? And recall that x 2 = x for positive x , then we can simplify the expression ( x + 4 ) 2 to just x + 4 instead. But wait, we still need to subtract it by x right? What's left is just ( x + 4 ) − x = 4 and that's your answer!
Alternatively, here's another short solution:
Let y = x 1 , then when x → ∞ , y → 0 , the limit becomes
y → 0 lim y 2 1 + y 8 + 1 − y 1 = y → 0 lim y 1 + 8 y + y 2 − 1
What's left to do is to apply L'hopital's rule : Differentiate top and bottom (separately) and we get,
y → 0 lim 2 1 + 8 y + y 2 2 y + 8 = 2 1 + 8 ( 0 ) + 0 2 2 ( 0 ) + 8 = 4
as well!
Log in to reply
@Pi Han Goh – Thanx for this wonderful solution!
Log in to reply
@Arkajyoti Banerjee – So the catch of this method is that subtracting a small number from an infinitely large number is ignorable while evaluating a function's limit while it tends to infinity, right? Because it hardly affects that infinitely large number
If ( x + 4 ) 2 , then it is ∣ x + 4 ∣ .
@Arkajyoti Banerjee 1 = ± 1 . not 1 .
Take a look. Part 1: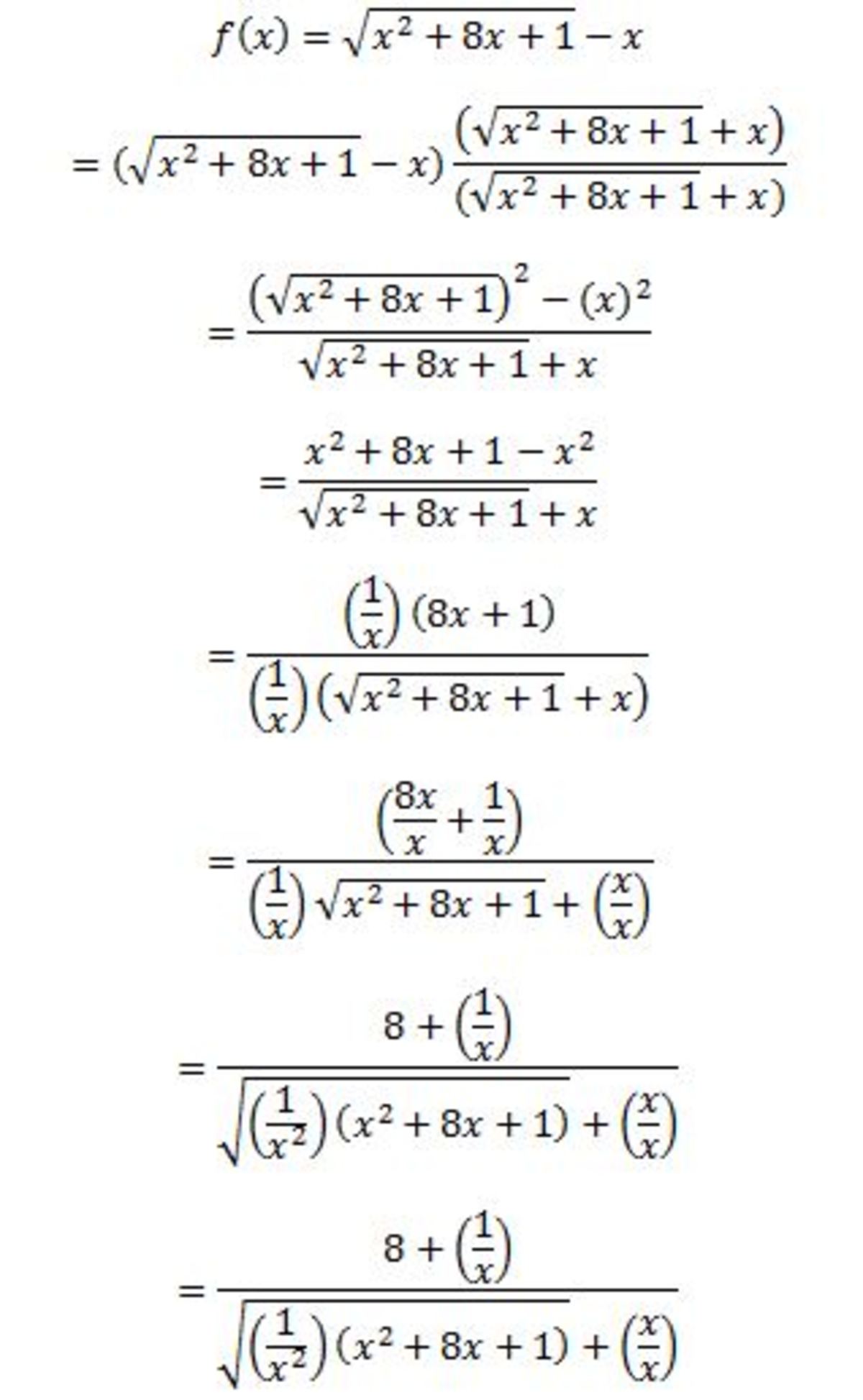 Part 2:
Part 2: