Is the Motion Simple Harmonic?

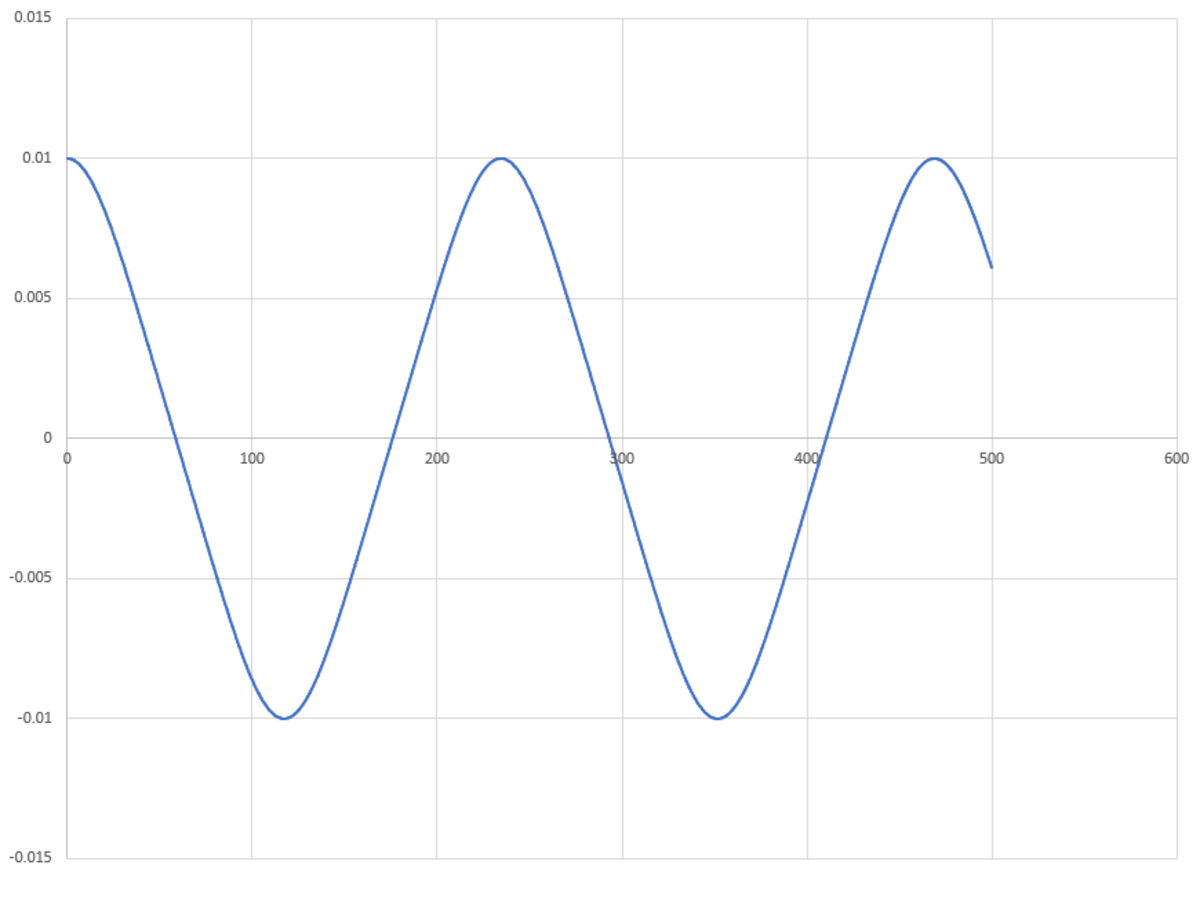
The answer is false.

The equation of motion for a simple harmonic oscillation is: $\ddot{x} + \omega^2 x = 0$

The equation of motion, for small displacements, for the given system is:

$\ddot{x} + kx^3 = 0$

The movement of the mass is confined along the x-axis due to the symmetry in the situation and the motion is oscillatory in nature. However, the equation of motion does not fit the same structure as that of a harmonic oscillator.

Say the block has moved a distance $x$ to the right along the x-axis. At this instant of time, The length of each spring is:

$L_s = \sqrt{x^2 +1}$

The total potential energy of the system is:

$V = 2\left(\frac{1}{2}k\left(L_s - 1\right)^2\right)$

The kinetic energy of the block is:

$T = \frac{1}{2}\dot{x}^2$

The total energy of the system is conserved and is:

$E = T + V$

Since the energy is constant, the above expression can be differentiated with respect to time and equated to zero: $\frac{dE}{dt} = 0$

Performing the calculation and simplifying gives:

$\ddot{x} + \frac{2\,k\,x\,\left(\sqrt{x^2+1}-1\right)}{\sqrt{x^2+1}}=0$

Now, we consider the case where the displacements are small ( $x<<1$ ). This can be considered by expanding the terms $\sqrt{x^2+1}$ and $\frac{1}{\sqrt{x^2+1}}$ , and neglecting higher powers of $x$ . By doing so:

$\ddot{x} + 2kx\left(1+\frac{x^2}{2}-1\right)\left(1 - \frac{x^2}{2}\right) =0$

Neglecting the $x^5$ term leads to:

$\ddot{x} + kx^3 = 0$