Is there a neat way to solve this one?

1728=12^3<2020<12^(3,5)=3456*sqrt(3), hence 3<log_12(2020)<3,5. So the answer is 3.

We can easily calculate that $12^3=1728<2020$ and $12^4=20736>2020$ . So $4\log 12>\log 2020>3\log 12$ or $3<\log_{12} 2020<4$ . Hence $\lfloor \log_{12} 2020\rfloor=\boxed 3$ . Since the difference between $2020$ and $20736$ is much larger than the difference between $2020$ and $1728$ , $[\log_{12} 2020]=\boxed 3$ .

It is only neat to know calculating logarithms with continued fractions . Not neat at all to do the computations. Let $x=\log_{12} 2020$ , then $2020 = 12^x$ and we can express $x$ as a continued fraction as follows:

$x = n_0 + \frac 1{n_1 + \frac 1{n_2 + \frac 1{n_3+\frac 1\cdots}}}$

And the $n_k$ are given by: $12^{n_0} < 2020 < 12^{n_0+1}$ or $n_0= \lfloor \log_{12} 2020 \rfloor = 3$ , $n_1 = \left \lfloor \log_{\frac {2020}{12^3}} 12 \right \rfloor= 15$ , $n_2 = \left \lfloor \log_{\frac {12}{\left(\frac {2020}{12^3}\right)^{15}}} \frac {2020}{12^3} \right \rfloor= 1$ ... As can be seen it is a very complicated way to calculate $\log_{12} 2020$ and I used an Microsoft Excel spreadsheet to implement the computations.

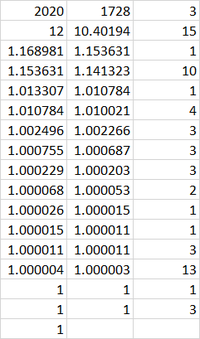
$\log_{12}(2020)$ can be written as a continued fraction as such, as you can see the result is equal to $3$ after rounding.