Is there something special about pentagons?
What is the fraction of regions in orange to the area of the pentagon?
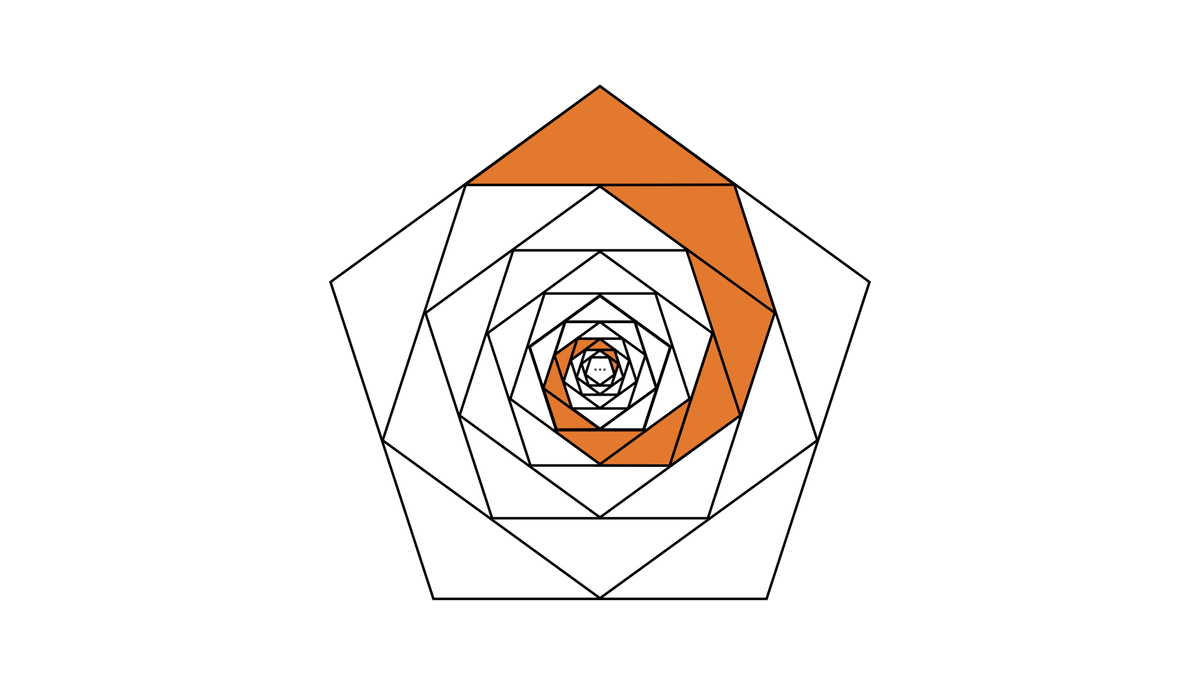
Note: The dots indicate that the coloring continues
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Wow, that's very pretty. What did you use to create the animation?
Log in to reply
Thanks, Chris! I used keynote. I hope to upload a video about generalizing this with many polygons on my youtube channel
There is nothing special about pentagons... it is true for any polygon with n sides. Do the same to get the answer as n 1
Log in to reply
Or just note that in each ring of n triangles, exactly one of them is orange. But where's the nice animation in that? ;-)
Log in to reply
Yes, I agree. I thought of that too. But, it's not so elegant.
Log in to reply
Thanks.
P.S. I don't know why, but the more I stare at the animation, those 5 individual areas look like a chameleon tail to me...
(edit) golden ratio?
Log in to reply
Oh you got me.. I was trying to remember 'chameleon', I couldn't get it..
Let the pentagon have an area of 5, each chameleon would have an area of 1,
Area of one chameleon = 2 s sin 3 6 ° [ 1 + cos¹ 3 6 ° + cos² 3 6 ° + cos³ 3 6 ° + . . . . ] × 2 s [ cos¹ 3 6 ° + cos² 3 6 ° + cos³ 3 6 ° + . . . . ]
Which when put equal to 1 gives s≈1.8
And a pentagon with area 5 has a side of ≈1.7 I don't know where the error is but it works.
(The infinite series has a sum of 4.23606... exempting 1, on wolfram it shows the sum is √ 5 − 3 − 1 − √ 5 )
So it's worth noting that cos 36 is 2 ϕ , and it is what leads to the progression.
Log in to reply
@A Former Brilliant Member – Interesting indeed...
So yeah there is golden ratio, but as you said there's nothing special about pentagons, I'm not sure but maybe there's rarely the golden ratio otherwise
The green one look's especially like a chameleon's tail lol @Mahdi Raza
nice animation @Mahdi Raza
Nice animation! How long did it take? :)
Log in to reply
I think more than 4hours ... @Mahdi Raza
Thanks, Vinayak! I reckon not more than 1 - 1.5 hours
Log in to reply
ooh..if I was there in your place I would take almost 5 hours or less than that.........:)
Greetings, mention[7354641:Mahdi Raza]. I am trying to create an animation for my problem Colliding Spring System . Would you be willing to help me by any chance? Your animation here is wonderful.
Log in to reply
Log in to reply
Thanks for your help. You are so kind. Can I call you Pi?
Thanks! I checked your problem, tried to understand a bit but I give hope. I don't know how to begin... and also what kind of animation you will make it into. Yet to learn this advanced stuff, sorry...
Log in to reply
That is very nice of you to try. I am not picky about the way the animation will look. If I post a solution, do you think that will help you understand it better? I haven't tried to solve the system yet. I will try to do that today as well.
Log in to reply
@James Wilson – Sure! it'll help me to understand the problem and what it means to say a bit better
Log in to reply
@Mahdi Raza – I'm working on that as we speak.
@Mahdi Raza – I posted a solution. I left some steps to the reader, but I showed the concept of the solution. Now I will work on setting values for the parameters and coming up with a solution for that.
@Mahdi Raza – Update: I'm struggling finding a solution to the linear system of ODEs because it does not have a full set of eigenvectors. My textbook does not say how to handle that.
@Mahdi Raza – Update 2: I found an example in my textbook like this one. I will let you know when I have the solution. I took k 1 = 2 , k 1 = 1 , l 1 = 1 , l 2 = 1 . 2 5 , m 1 = 3 , m 2 = 1 .
@Mahdi Raza – Update 3: It turns out this example is not quite like the example in the textbook, since A is both singular and does not have a full set of eigenvectors. The example in the textbook has A nonsingular. I may need additional help. Sorry about that. I hate to make you wait.
@Mahdi Raza – Update 4: I'm sorry for spamming your comments here, but the example in the textbook was more like this problem than I thought. I was mistaken again. So I think I can do this given enough time. I'll try to have it completed within 24 hours. Thanks again for your interest.
@Mahdi Raza – Update 5: After solving the linear system of ODEs, I got the following solution with u = 1 : x 1 = 4 3 t − 1 6 3 2 sin 3 2 2 t and x 2 = 4 9 + 4 3 t − 1 6 9 2 sin 3 2 2 t for 0 ≤ t < 2 2 3 π . Here's the part that doesn't make sense. For t ≥ 2 2 3 π , I'm getting x 1 ′ = 1 and x 2 ′ = 2 3 . I don't see how this is possible, as it violates the conservation of energy, so I must have made a mistake somewhere. I will take another look at this tomorrow. I might need to get some outside help.
The following will be a more or less formal proof with the downside that it might not be entirely intuitive.
Let A k be the area of the k -th inner pentagon (and A 0 is the area of the outer pentagon).
First, look at the outer and first inner pentagon. The inner pentagon leaves 5 equally-sized triangles and 1 of them is colored, so the colored area in the first step is 5 1 ⋅ ( A 0 − A 1 ) So the ratio of colored area to the whole area is A 0 5 1 ⋅ ( A 0 − A 1 ) = 5 1 ⋅ ( A 0 A 0 − A 0 A 1 ) = 5 1 ⋅ ( 1 − A 0 A 1 )
Second, also consider the second inner pentagon. It leaves 5 equally-sized triangles in the first inner pentagon and 1 of them is colored, so now the colored area is 5 1 ⋅ ( A 0 − A 1 ) + 5 1 ⋅ ( A 1 − A 2 ) = 5 1 ⋅ ( A 0 − A 2 ) So in the second step we have the ratio: A 0 5 1 ⋅ ( A 0 − A 2 ) = 5 1 ⋅ ( 1 − A 0 A 2 )
Continuing this, we get for the colored area in the k -th step: i = 1 ∑ k 5 1 ⋅ ( A i − 1 − A i ) = 5 1 ⋅ i = 1 ∑ k ( A i − 1 − A i ) Notice that the above sum is a telescope sum , so it simplifies to 5 1 ⋅ ( A 0 − A k ) So the ratio in the k -th step is A 0 5 1 ⋅ ( A 0 − A k ) = 5 1 ⋅ ( 1 − A 0 A k ) Since k → ∞ lim A k = 0 (the area of the inner pentagon gets infinitely small), if we continue infintely we get for the final ratio: k → ∞ lim 5 1 ⋅ ( 1 − A 0 A k ) = 5 1 ⋅ ( 1 − A 0 k → ∞ lim A k ) = 5 1 ⋅ ( 1 − 0 ) = 5 1
Bonus: Replace "Pentagon" with " n -gon" and 5 1 with n 1 to generalize the proof.
Brilliant! You wrote the idea very nicely, converting the mess into a clean telescopic formula. Upvoted!!
And "Not all problems have such an intuitive aspect", I second your comment.
At the outermost boundary, one in five congruent triangles is colored, the same happens inside infinitely, so the ratio remains 5 1
Create 5 copies of the area we want to find, and rotate them to fit inside the pentagon perfectly. We obtain 5 such copies which are equal in area and make up the whole area of pentagon