Is this even possible?
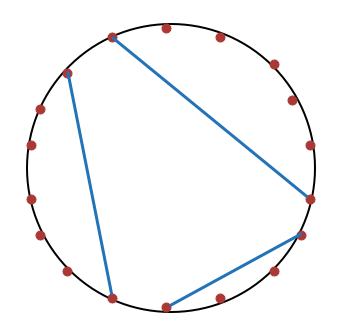 Let 18 equally spaced points be chosen on the circumference of a circle.
Let 18 equally spaced points be chosen on the circumference of a circle.
How many ways can these points be connected in pairs such that the resulting 9 segments do not intersect?
Note: Rotations are reflections are considered distinct arrangements.
The answer is 4862.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The problem clearly states that the points are on the circle, and not necessarily on the circumference of the circle.
Log in to reply
For "equally spaced points" to make sense, you will need them to lie on the circumference.
Also, if the points lie "within" the circle, it's possible that the 18 points are in a straight line, in which there is only 1 solution. I have updated the problem statement to reflect this.
Log in to reply
I see, thanks for the image
I s there any other solution possible using permutation and combination ?
Nice problem!! I was adding manually! By calculating each a i !! Calculation mistake! Got 4560... Bad luck!
A circle is defined as a set of points equidistant from a set of points. Points inside the circle aren't included in the set of points that consists of the circle.
How did u get to the last step? Can u plz explain?
Why can't I just say choose 6 points and they have 2 ways to build 3 non-intersecting lines ?
http://www.iro.umontreal.ca/~pift2125/Current/Notes/catalan.pdf
We assign values to the points in a order like this 1 , 2 , 3 , . . . . . 1 8 . Now, suppose that whenever two points 1 ≤ i < j ≤ 1 8 are connected with a line segment we say that we give i the value 1 and j the value − 1 . And, its notable that if no two such line segments l i j doesn't intersect there will be a the property like this a 1 + a 2 + . . . . a k ≥ 0 fro all k ≤ 1 8 . Hence, there are total C 9 = 4 8 6 2 ways of getting this.
Here is the general solution for this problem (here, n = 9 ):
Let the number of ways for 2 n points be a n . Choose one of the points and label it M . Then, M must be joined to a point, say N , such that there are even number of points on either side of the segment M N . This gives us the recurrence relation (yeah, another recurrence XD) : a n = a 0 a n − 1 + a 1 a n − 2 + . . . + a n − 1 a 0 , a 0 = 1 Let b n = a n − 1 where n ≥ 1 . Thus, b n = b 1 b n − 1 + b 2 b n − 2 + . . . + b n − 1 b 1 , b 1 = 1 Hence, we obtain the equations b n = n 1 ( n − 1 2 n − 2 ) and a n = b n + 1 which is the same as the n th Catalan number.