Isosceles Triangle And Peculiar Point Reloaded
A B C is an isosceles triangle with A B = A C , ∠ B A C = 9 6 ∘ . D is a point such that ∠ A C D = 4 8 ∘ , A D = B C and angle D A C is obtuse. What is the measure (in degrees) of ∠ D A C ?
The answer is 102.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Just to point out, what is the difference between this problem and the problem from which the inspiration was?
Log in to reply
The original problem:
 the original
the original
The inspired problem:
 the insprired
the insprired
Log in to reply
Angle DAC is obtuse in both cases. If there is no difference in the wording of the problem, how can the diagrams be different?
Log in to reply
@Shourya Pandey – There is a slight difference in the wording of the problem.
In the original says : ∠ D C A = 4 8 ∘
In the inspired says : ∠ A C D = 4 8 ∘
While it's the same angle, it could be oriented either clockwise or anticlockwise.
Log in to reply
@Abdelhamid Saadi – But you could draw ABC clockwise or anti-clockwise, so I don't get what convention you chose.
Log in to reply
@Shourya Pandey – I think there is no universal convention for oriented angles.
I follow the same convention as in GeoGebra.
Although you claim that the problems are different, I solved both in exactly the same way.
Log in to reply
Your proof works for both cases, and with the same result. By this problem I want to point out this symmetry.
But not all the proofs will work for both cases.
A very clever proof by Calvin Lin won't work directly without a little tweak.
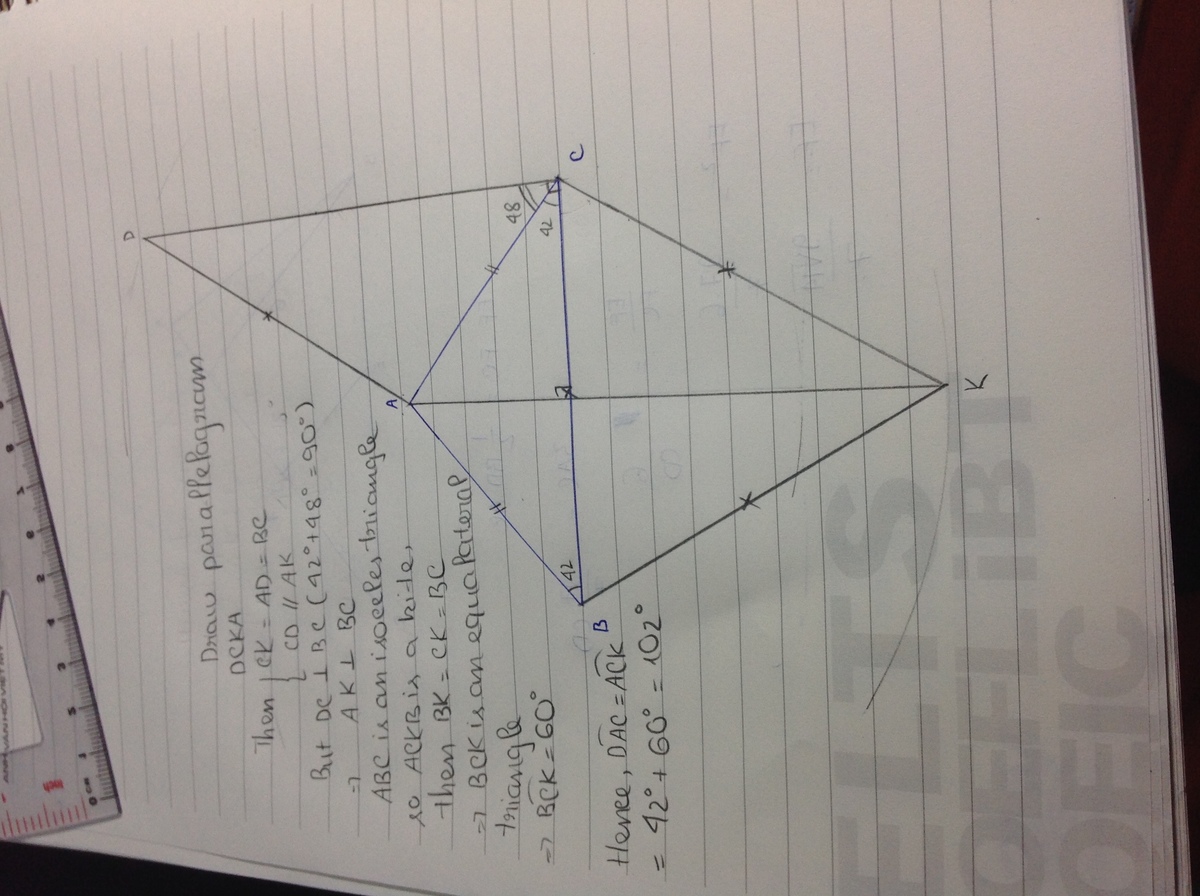
Consider a point E such that A E ⊥ B C , then E is a midpoint of B C .
Similarly, consider a point F such that A F ⊥ C D , then ∠ C A F = 9 0 ∘ − 4 8 ∘ = 4 2 ∘ .
Figure above shows that the two triangles A F C and B E A are similar.
Then, B E A F = A B C A = 1 ( ∵ A B = A C ) .
Therefore, A F = B E = 2 1 B C = 2 1 A D ( ∵ A D = B C ) .
Triangle A F D is right angle at F , thus ∠ D A F = 6 0 ∘ .
∠ D A C = 6 0 ∘ + 4 2 ∘ = 1 0 2 ∘ .