It Telescopes?
Let { a n } be a sequence of real numbers satisfying { a 0 = 1 a n + 1 = 4 + 3 a n + a n 2 − 2 for n ≥ 0 . Let S = n = 0 ∑ ∞ a n .
- If S converges, submit your answer as ⌊ 1 0 0 S ⌋ .
- If S diverges, submit your answer as − 1 .
This problem is based on a recent Putnam contest problem.
The answer is 500.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Large nitpick: All elements of a sequence being strictly less than 1 does NOT imply that the limit of that sequence is strictly less than 1.
Log in to reply
It is ∣ ∣ ∣ a n a n + 1 ∣ ∣ ∣ < 1 not just a n < 1 .
Log in to reply
∣ ∣ ∣ ∣ a n a n + 1 ∣ ∣ ∣ ∣ < 1 for all n ≥ 0 ⟹ n → ∞ lim ∣ ∣ ∣ ∣ a n a n + 1 ∣ ∣ ∣ ∣ < 1 .
Let a n = n 1 . Then ∣ ∣ ∣ ∣ a n a n + 1 ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ n 1 n + 1 1 ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ n + 1 n ∣ ∣ ∣ ∣ = n + 1 n < 1 for all n ≥ 0 .
But n → ∞ lim ∣ ∣ ∣ ∣ a n a n + 1 ∣ ∣ ∣ ∣ = n → ∞ lim n + 1 n = 1
Log in to reply
@Daniel Juncos – But it is shown that 4 3 < a n a n + 1 < 1 , which means that a n a n + 1 is bounded.
Log in to reply
@Chew-Seong Cheong – Would you agree that 4 3 < n + 5 n + 4 < 1 for all n ≥ 0 ?
Log in to reply
@Daniel Juncos – Thanks, I get what you mean now. But how do I resolve my solution.
Log in to reply
@Chew-Seong Cheong – You've already shown that a n is positive and strictly decreasing. You can show that it converges to 0 and take take the limit as a n approaches 0 in your expression for R .
Log in to reply
@Brandon Monsen – This is correct. Then you can use this to show that a n a n + 1 goes to 4 3 .
Log in to reply
@Daniel Juncos – Thanks, I got it now.
Log in to reply
@Chew-Seong Cheong – Closer, but still not exactly. Just because a sequence is bounded does not mean its limit exists. And just because a sequence is bounded below by 0 and is strictly decreasing does not mean its limit is zero.
Log in to reply
@Daniel Juncos – Thanks again. I have worded it as n → ∞ , a n 2 → a n + 1 2 . Not assuming that n → 0 lim a n = 0 . If the limit is 0, then a n a n + 1 is not defined.
Small nitpick: The ratio test is valid for ∣ R ∣ < 1 , where R = a n a n + 1 . It would be a good idea to give a lower bound for R , since R = − 3 satisfies the condition you gave (that R < 1 ), but the series would diverge.
Log in to reply
Thanks, you are right. I will change the solution.
Relevant wiki: Telescoping Series - Sum
In the form given by the problem, we can see that if a n > 0 , then a n + 1 > 4 − 2 = 0 ⇒ a n + 1 > 0 . Since a 0 > 0 , it follows that a n > 0 by induction on n .
Now, rearrange the recurrence relation to get ( a n + 1 + 2 ) 2 = ( a n + 2 ) 2 − a n . In this form, it is easy to see that ( a n + 1 + 2 ) 2 < ( a n + 2 ) 2 since a n > 0 . It follows that a n + 1 < a n
We now know that a n is a strictly decreasing sequence of positive reals, and so a n must converge to some limit 0 ≤ L < a 0 . Thus, we have that ( L + 2 ) 2 = ( L + 2 ) 2 − L ⇒ L = 0
Rearrange again to get ( a n + 2 ) 2 − ( a n + 1 + 2 ) 2 = a n , and so S can be written as a telescoping sum:
S = n = 0 ∑ ∞ a n = n = 0 ∑ ∞ [ ( a n + 2 ) 2 − ( a n + 1 + 2 ) 2 ] = p → ∞ lim ( a 0 + 2 ) 2 − ( a p + 2 ) 2 = 5
So ⌊ 1 0 0 S ⌋ = 5 0 0
Relevant wiki: Convergence - Ratio Test
While the other solutions have arrived at the correct limit, I don't believe the mechanics behind either are entirely rigorous.
First, it can be easily shown through induction that a n > 0 , ∀ n ∈ N .
Then, 4 + 3 a n + a n 2 < 4 + 4 a n + a n 2 ⟹ a n a n + 1 < 1 ⟹ a n + 1 < a n .
Since a n is decreasing and bounded below, then there is some a ≥ 0 such that a n → a as n → ∞ .
Now we can treat this limit algebraically. From a n + 1 = 4 + 3 a n + a n 2 − 2 , send n to infinity on both sides and we get
a = 4 + 3 a + a 2 − 2 ⟹ 4 a = 3 a ⟹ a = 0 .
To see if ∑ a n converges, we can perform the ratio test:
∣ ∣ ∣ ∣ a n a n + 1 ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ a n 4 + 3 a n + a n 2 − 2 ⋅ 4 + 3 a n + a n 2 + 2 4 + 3 a n + a n 2 + 2 ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ 4 + 3 a n + a n 2 + 2 3 + a n ∣ ∣ ∣ ∣ , since a n = 0 .
Since a n → 0 , then n → ∞ lim ∣ ∣ ∣ ∣ a n a n + 1 ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ 4 + 3 ( 0 ) + 0 2 + 2 3 + 0 ∣ ∣ ∣ ∣ ∣ = 4 3 .
Since this limit is strictly less than 1 , then ∑ a n converges absolutely to some real number. We can now treat THAT limit algebraically as well.
Let A = ∑ a n . Then A − 1 = ∑ a n + 1 .
Since ∑ a n converges and all a n > 0 , then there must be some N such that for all n ≥ N we have a n < 1 .
This means that for all n ≥ N we have a n 2 < a n ; i.e. ∑ a n 2 converges as well.
Let B = ∑ a n 2 . Then B − 1 = ∑ a n + 1 2 .
Finally, we have
a n + 1 = 4 + 3 a n + a n 2 − 2 ⟹ a n + 1 2 + 4 a n + 1 = a n 2 + 3 a n ⟹ ∑ a n + 1 2 + 4 ∑ a n + 1 = ∑ a n 2 + 3 ∑ a n ⟹ B − 1 + 4 ( A − 1 ) = B + 3 A ⟹ A = 5
Good explanation
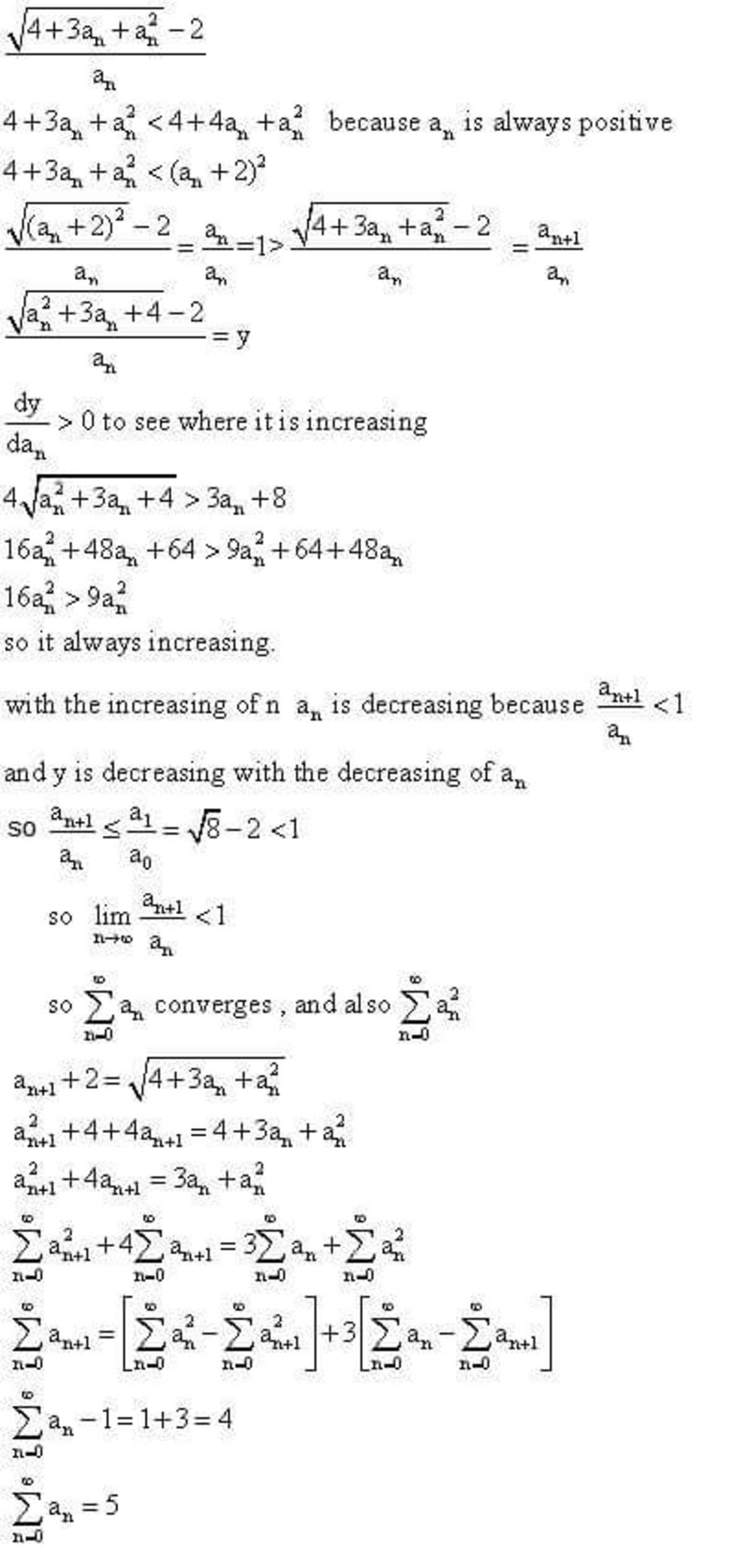
Relevant wiki: Convergence - Ratio Test
a n + 1 a n + 1 + 2 ( a n + 1 + 2 ) 2 a n + 1 2 + 4 a n + 1 + 4 a n + 1 2 + 4 a n + 1 = 4 + 3 a n + a n 2 − 2 = 4 + 3 a n + a n 2 = 4 + 3 a n + a n 2 = a n 2 + 3 a n + 4 = a n 2 + 3 a n
From the above, we note that if a n > 0 , then 0 < a n + 1 < a n . Since a 0 = 1 , we have 0 < a n < a 0 = 1 . This means that a n is strictly decreasing and that as n → ∞ , a n → 0 . From a n + 1 2 + 4 a n + 1 = a n 2 + 3 a n , and as n → ∞ then a n 2 → a n + 1 2 , ⟹ 4 a n + 1 = 3 a n , ⟹ a n a n + 1 = 4 3 .
Therefore, ⟹ n → ∞ lim ∣ ∣ ∣ ∣ a n a n + 1 ∣ ∣ ∣ ∣ = 4 3 < 1 and by ratio test n = 0 ∑ ∞ a n converges. Then, we have:
a n + 1 2 + 4 a n + 1 ⟹ a n + 1 2 − a n 2 + 4 ( a n + 1 − a n ) + a n n = 0 ∑ ∞ ( a n + 1 2 − a n 2 ) + 4 n = 0 ∑ ∞ ( a n + 1 − a n ) + n = 0 ∑ ∞ a n − a 0 2 − 4 a 0 + S ⟹ S = a n 2 + 3 a n = 0 = 0 = 0 = a 0 2 + 4 a 0 = 5 Note that a 0 = 1
⟹ ⌊ 1 0 0 S ⌋ = 5 0 0