It will all click together

Let $\angle BAD=\alpha$ . Triangle ABD is isosceles, so $\angle ADB=\angle ABD=90^{º}-\frac{\alpha}{2}$ and $\sin\left(90^{º}-\frac{\alpha}{2}\right)=\cos\left(\frac{\alpha}{2}\right)$ .

Now we calculate $\cos\left(\frac{\alpha}{2}\right)=\sqrt{\frac{1+\cos\alpha}{2}}$ $\Rightarrow$ $\cos\left(\frac{\alpha}{2}\right)=\frac{\sqrt{3}}{3}$

By using Law of sines:

$\displaystyle \frac{1}{\cos{\frac{\alpha}{2}}}=2R \Rightarrow R=\frac{\sqrt{3}}{2}$

$\therefore \lfloor 1000R \rfloor = \boxed{866}$ .

First, using the Cosine rule we have that

$(BD)^{2} = (AB)^{2} + (AD)^{2} - 2*(AB)*(AD)*\cos(\angle BAD) =$

$2 - 2*(-\frac{1}{3}) = \frac{8}{3} \Longrightarrow BD = \sqrt{\frac{8}{3}}$ .

Now let $CD = \cos(\angle ABC) = x$ . Since $ABCD$ is cyclic we have that

$\cos(\angle ADC) = -\cos(\angle ABC) = -x$ and

$\cos(\angle BCD) = -\cos(\angle BAD) = \frac{1}{3}$ .

Next, since $\Delta ABC$ and $\Delta ADC$ have chord $AC$ in common, we can use the Cosine rule to set up the following equation:

$1^{2} + x^{2} - 2(1)(x)\cos(\angle ADC) = 1^{2} + (BC)^{2} - 2(1)(BC)\cos(\angle ABC)$

$\Longrightarrow 1 + x^{2} - 2x*(-x) = 1 + (BC)^{2} - 2(BC)(x)$

$\Longrightarrow (BC)^{2} - 2x*(BC) - 3x^{2} = 0 \Longrightarrow (BC - 3x)(BC + x) = 0.$ .

Now since $BC \gt 0$ we have that $BC = 3x$ . But since the sides $DC$ and $BC$ are in the ratio $x : 3x \Longrightarrow 1 : 3$ and $\cos(\angle BCD) = \frac{1}{3}$ we can conclude that $\Delta BCD$ is a right triangle with $\angle BDC = 90^{\circ}$ . This implies that $BC$ is a diameter of the circle in which $ABCD$ is inscribed.

Using Pythagoras, we then have that

$(BC)^{2} = (CD)^{2} + (BD)^{2} \Longrightarrow 9x^{2} = x^{2} + \frac{8}{3} \Longrightarrow x^{2} = \frac{1}{3}$ ,

and since $x \gt 0$ we have that $BC = 3x = \sqrt{3}$ .

Thus $R = \frac{BC}{2} = \frac{\sqrt{3}}{2} = 0.8660254....$ , and so $\lfloor 1000*R \rfloor = \boxed{866}$ .

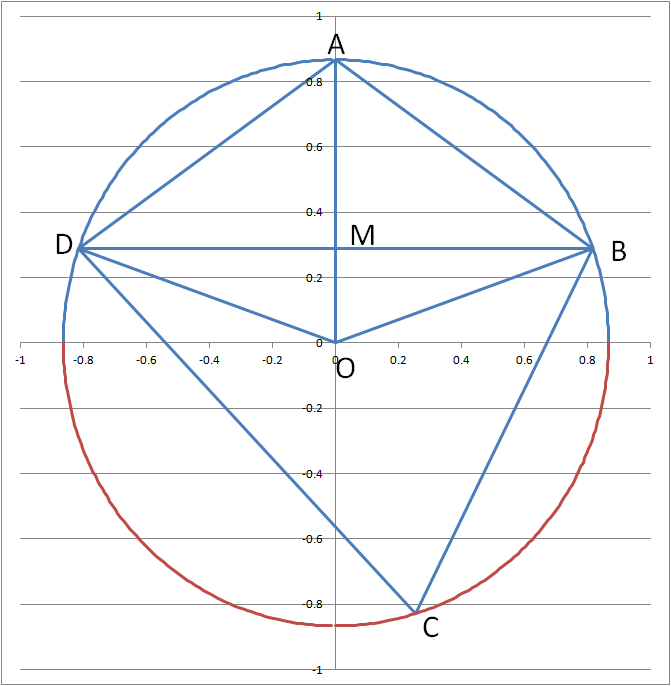
Let the circumcenter be $O$ and $\angle BAD = \alpha$ . Using Cosine Rule, we have:

$\quad BD^2 = 1+1-2\left( -\frac {1}{3} \right) = \frac {8}{3} \quad \Rightarrow BD = 2 \sqrt {\frac {2}{3} }$

Since $\triangle ABD$ is an isosceles triangle, $O$ must be on the perpendicular from $A$ to $BD$ (see figure below). Let the foot of the perpendicular be $M$ . Then we note that:

$\quad OB^2 = OM^2+BM^2\quad \Rightarrow R^2 = (R-AM)^2 +BM^2$

We note that:

$\quad BM = \frac {1}{2} BD = \sqrt {\frac {2}{3}}\space$

$\quad AM^2 = AB^2 - BD^2 = 1 - \frac{2}{3} = \frac {1}{3} \quad \Rightarrow AM = \frac {1}{\sqrt{3}}$

$\quad \Rightarrow R^2 = (R-AM)^2 +BM^2 = (R-\frac {1}{\sqrt{3}})^2 +\frac {2}{3}$

$\quad \Rightarrow R^2 = R^2-\frac {2}{\sqrt{3}}R + \frac{1}{3} +\frac {2}{3}\quad \Rightarrow R = \frac {\sqrt{3}}{2}$

$\quad \Rightarrow \lfloor 1000*R \rfloor = \boxed{866}$

If Someone Knows The Formula for Circum-Radius of an Triangle Then It would be more Easy . However it is Not Pure Mathematical , (Because We Use Just Known Formula) But Brian Sir's Solution is Pure Mathematical . But for Sake of Variety :

Using Cosine Rule , in Triangle ABD ; $\displaystyle{(BD)^{ 2 }=(AB)^{ 2 }+(AD)^{ 2 }-2\times (AB)\times (AD)\times \cos (\angle BAD)\\ BD=2\sqrt { \cfrac { 2 }{ 3 } } \quad }$ . Using Standard formulas : $\displaystyle{R=\cfrac { abd }{ 4\Delta } \\ \Delta =\sqrt { S(S-a)(S-b)(S-d) } \\ a=2\sqrt { \cfrac { 2 }{ 3 } } \quad ,\quad b=1\quad ,\quad d=1\quad ,\quad S=1+\sqrt { \cfrac { 2 }{ 3 } } \\ S-a=1-\sqrt { \cfrac { 2 }{ 3 } } \quad ,\quad S-b=\sqrt { \cfrac { 2 }{ 3 } } \quad ,\quad S-d=\sqrt { \cfrac { 2 }{ 3 } } \\ \therefore \quad \Delta =\sqrt { (1+\sqrt { \cfrac { 2 }{ 3 } } )(1-\sqrt { \cfrac { 2 }{ 3 } } )(\sqrt { \cfrac { 2 }{ 3 } } )(\sqrt { \cfrac { 2 }{ 3 } } ) } =\cfrac { \sqrt { 2 } }{ 3 } \\ \therefore \quad \boxed { R=\cfrac { \sqrt { 3 } }{ 2 } } Ans.}$ .

Let B D be x and angle BAD be q, apply cosine rule,

Cos q = (1^2 + 1^2 - x^2)/ [2 (1)(1)] = -1/ 3 {The Cosine angle of a Tetrahedron.}

=> x^2 = 8/ 3.

Cos (2 Pi - 2 q) = (R^2 + R^2 - x^2)/ (2 R^2) = 1 - x^2/ (2 R^2)

R^2 = (x^2/ 2)/ (1 - Cos 2 q) = [(8/ 3)/ 2]/ [1 - (-7/ 9)] = 3/ 4

As Cos 2 q = 2 (Cos q)^2 - 1 = 2/ 9 - 9/ 9 = -7/ 9

R = Sqrt (3)/ 2 = 0.86602540378443864676372317075294

Floor (1000 R) = 866