It's an SAT question!
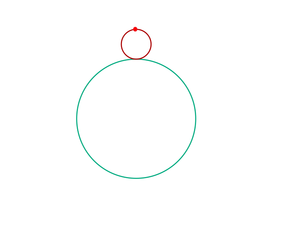 The radius of the smaller circle is
4
1
the radius of the larger circle. The smaller circle rolls around the larger circle for one trip, back to its starting point, without any slipping.
The radius of the smaller circle is
4
1
the radius of the larger circle. The smaller circle rolls around the larger circle for one trip, back to its starting point, without any slipping.
How many times would the red dot on the smaller circle rotate around the center of the smaller circle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
The CENTRE of the small coin needs to travel around a circle of radius 4+1=5cm. So the CENTRE needs to travel 10pi, as though it is traveling along a straight line of length 10pi while revolving. This gives the solution.
Log in to reply
yes only your explanation is understandable.
This one took a while for me to wrap my brain around why the answer could possibly be 5. I was so sure that it was four, and I didn't see how there could be any difference between rolling the smaller circle around a larger circle and rolling it along a line of the same length as the circumference of the circle. Hopefully this explanation sheds some light on why the answer is 5:
Let's pretend the smaller circle is a quarter. We start with the top of George Washington's head facing upward, at the top of the larger circle. After traveling for the entire circumference of the quarter, the coin will be 1/4 of the way around the larger circle with the same part of the quarter in contact with the circle (the bottom of Washington's neck) but since we are now on the right side of the quarter, you will notice that the top of Washington's head is pointing to the right. If the coin only went through exactly one revolution then we would expect to see the coin in the same orientation as the start (head pointing upward). It turns out that since the larger circle slopes away from the coin, the quarter picks up an extra 1/4 of a revolution each time it travels 1/4 of the way around the larger circle. These four quarter-revolutions add up to the extra revolution.
Log in to reply
Excellent explanation Walker..
Thank you, Fabio Gama: your response makes much sense to me. Although my initial response was incorrect, I now see my error in selecting 4. Four revolutions of the small circle would cover the circunference of the large circle, but if the small circle were to reoccupy its starting position, it would have to make a fifth revolution to get there. Hence, 4+1 = 5.
Actually you can solve this by physical intuition.
If the small circle is to roll around without slipping(that's it rolls and touch large circle by one point to one point). We'll have the distance travel by the center of small circle is equal to the number of revolution times the perimeter of small one.
then we have
N × 4 r = 4 r + r
So N = 5
the answer is 4. let the redius of the bigger circle is r, so the circumference of smaller circle is 2* Pi* r/4, and the circumference of the bigger circle is 2 Pi r, and the ratio of circumference of smaller to bigger circle is 4, so the circumference of the bigger circle is 4 times bigger than the bigger circle, so if the smaller circle is to roll around the bigger untill the starting point then , it can encircle only 4 times.
Log in to reply
I reached the same solution. But, I was a hesitant to give the answer because it was a question of logic level 4
The answer is actually 5. I thought 4 initially also. Let's say the circumference of the larger circle is 4 and the circumference of the smaller circle is 1. If you roll the smaller circle in a straight line, it has to rotate 4 times to go 4 units (the circumference of the bigger circle). However, if you take that linear trajectory and bend it into a circle with circumference 4, you have added a rotation. The smaller circle must rotate one extra time to go around the big circle, not because the distance is greater but because its path rotates. I envision it this way. Imagine the small circle traveling along a 4 unit line segment. Now take the end of that line segment where the small circle is sitting and rotate it to meet the beginning of the line making a large circle. In order to do this, the small circle on the end of the line rotates 1 time.
Log in to reply
But the name for that particulat motion (making the fifth here) is revolution. The smaller circle rotates four times and revolves around the larger once. Rotates is about the object's own center of mass while revolutions are around an external COM. Food for thought
4 and 5 are both true depending on how you are interpreting the question.
With respect to the larger circle, the answer is 4. The initial contact point of the smaller circle makes contact with the larger circle 4 times to get back to the starting position.
But with respect to the page, by the time the initial contact point makes contact again the smaller circle's position is not purely translated from the initial position. There is an additional 1/4 turn.
So the path is 4 rotations, but if you watched the starting point it goes around 5 times.
I also reached to the same conclusion...
Log in to reply
So did I but then I watched this YouTube video
https://www.youtube.com/watch?v=kN3AOMrnEUs
It said that the general equation for this sort of problem is that the radius of the smaller circle is 1/n of the larger circle. The answer is n+1 ... I think!!!
Log in to reply
@Ayush Premchand – Thanks for the link Ayush, I made a mistake in the asnwer, just working out the circumfrences. The video is the perfect guide.
If you want to think this way, you have to beware 'cause when the circle roll forward the distance that matter is the distance that center undergo not the circumstance.
People get the two mixed up since for solution=5 you have this that answers the revolution or the center rotating of the small circle around the 4 time radius larger circle, otherwise it should mean the amount of separate iterations the small circle undergoes in the physical sense per se. However it is in Physics found by the work that it makes the central force's from the larger circle transmit the spin to the dot in the smaller circle. The central force rotates the dot by 5/4 radiusX2pi=5/2radiusXpi. The frequency of spin in the smaller circle around its center however is equal to 2radius pi smaller than the circular spin making it 5 times around.
 Compare Rotation & Revolution
Compare Rotation & Revolution
Log in to reply
As Alimun has demonstrated above, the answer to the question "as asked" is 4. It asks for revolutions, not rotations.
Log in to reply
To be clear, I might have to revise my answer explanation below, which I think is a little confusing. So really only need to change the last sentence question becomes "how many times the smaller circle will "rotate" in total for "one lap around" or "one round revolve" the bigger circle?
How did you get 4 r + r on R.H.S ?
Log in to reply
Consider the motion of centre of mass of small sphere with respect to the large one.
What's wrong with this? The circumference of the big circle is $2\pi r,$ and that of the small one is $2\pi\frac{r}{4}=\frac{1}{2}\pi r.$ So one complete trip around the big circle is exactly 4 trips around the small one. It should be 4 revolutions of the small one.
Log in to reply
You should take into account the curvature of spheres since it's not linear so it has to take more distance to take a complete trip.
If the question asked how many rotations take place the answer would be 5 but it asked how many times the red point would touch he green circle so the correct answer is 4
The answer must be 4.The extra rotation will be about the centre of the larger circle not about the smaller one.But in question no. of revolution around the smaller circle is asked so answer should be 4.
This question has actually appeared in a Sat test, but the real topic of debate is how it's worded. You can look at it from two perspectives, the smaller circle's, and the larger circle's, each provides a separate answer.
However the wording in this particular question says "revolves" which I really don't care to explain why, but I believe the correct answer should be 4.
I do see the logic behind your answer, I'm just rather bored at the moment, and felt like sharing my opinion.
The question asked for rotations NOT rotations plus revolutions. The rotational distance travelled is 4 times its radius
No answer is not 4. Really first time I also thought like you but in a reality answer is 5. If you see motion of centre of small circle which rotate in 5r radius circle (r is a radius of small circle) and travel a 2π(5r). Now suppose a circle a radius with r motion in a straight line and it's centre travel a distance 2π(5r). Than tell me every of point circle how many round roll around the centre. Your answer is 5.
In general, if ratio of radii is n 1 , then the answer is ( n + 1 ) times.
Relevant: Coin Paradox .
Moderator note:
What is the intuition behind the extra revolution?
Quite interesting.
If the smaller coin is rolled on a straight line of the same length as that of the circumference of the larger circle, then answer will be 4.
When the smaller circle is rolled around the larger circle, there is extra change in the direction of the initial point due to continuously changing direction of the trajectory of smaller circle.
Also, if one observes the whole procedure seating at the center of the larger circle, then answer will be 4, same as in case of straight line.
Log in to reply
so let calculi it using example - let the smaller circle has r=2 so this mean that the larger has r=8 - from these result that the circumference of smaller will be equal 12,56 and the circumference of larger circle will be equal 50,24 - so 50,24/12,56 = 4 - but in the text have wrote that one trip back so what mean 4-1=3 - what possibility of answer not is there in the list of answers
Shouldn't the question be h How many rotations instead of revolutions?
Are you sure that its a SAT question?
Log in to reply
Pretty sure. Is The New York Times trustworthy?
It looks kind of like 2015 AMC 10 A # 14.
This is interesting! Really innocuous problem that stumped me for a few minutes. Extra turn results from the coin traveling in a circle around the center of the coin. So that, along with its obvious rotations. Definitely not obvious at first, however.
Let see the statement "one trip back to its starting point" in your question, "starting point" in a trip around the large circle can have two different definitions. The first definition is the position of the "starting point" of a small circle back attached to the circumference of a large circle (revolution), and the second definition is the position of the starting point of a small circle back line to its original position relative to the small circle at the beginning of the movement (rotation).
In your question doesn't explain what is meant by these two definitions, and of course, if it was not emphasized then the logic simply is intended more towards " some full turn" of small circle take the circumference of a large circle, instead of "a round of small circles filled to its own axis ". Not the case referred to in this video SAT question . This video clearly mentioned "how many time CIRCLE A REVOLVE in total"
So, "one trip back to its starting point" in your question can't be assumed equal to "rotation of cicle" but rather contain "revolution of cicle". So, for your question applies the formula "R" (the radius of big circle) devided by "r" (the radius of the small circle) generated from (2 * pi * R) / (2 * pi * r), whereas in video case SAT question is correct using the formula N = n + 1, because it is intended as a revolution of small circle against the full circumference of the large circle.
The answer for your question should be fixed 4 times because it refers to a revolution of small circle, whereas the sense of "a rotation of small circle" referred to in the video SAT question generate 5 times for the same case (the radius of the smaller circle is 1/4 the radius of the larger circle)
 Compare Rotation & Revolution on your case
Compare Rotation & Revolution on your case
Somehow I understand the video and I can accept it, but if I see it correctly, the same spots on the smaller circle only touched the bigger circle exactly 3 times in the video, in which I think it should be 3 full rotation in the video and 4 rotation in this case. But maybe I'm wrong
The answer is 4 Radius of small = 1/4 of large. But we are interested in the diameter, not the radius. So we multiplied by 8 to get the horizontal diameter. We had another 8 to get the vertical one. 8 + 8 = 16. 16 divided by 4 is 4 !!
@Pi Han Goh Could you please define what a rotate is?
Log in to reply
Rotate = move or cause to move in a circle around an axis or center.
Log in to reply
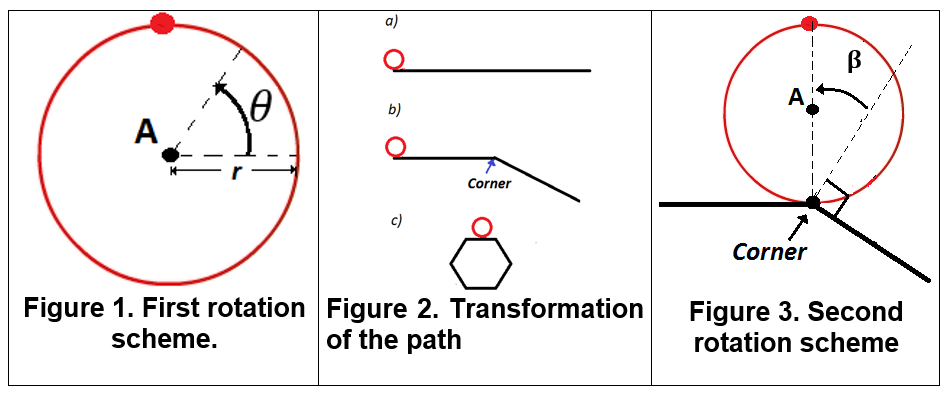
To describe a rotation requires two pieces of information (See Figure 1):
a) The centre A of the rotation
b) The angle θ of the rotation
In reference to answers to the problem, the value 1 . 0 means that the circle rotates 3 6 0 ∘ around the centre A . Now, if the circle rolls on a right line of a length L (See Figure 2-a), the circle rotates θ = 2 π r L ( 3 6 0 ∘ ) , where r is the radius of the circle. But, what happen if a corner divides the right line? (See Figure 2-b) In this case, the circle (including the centre A ) rotates an angle β < 3 6 0 ∘ around the corner (See Figure 3).
So, there will not be rotation of the circle around the centre A when the circle rotates around the corner .
Finally, if the circle rolls on a hexagon (See Figure 2-c), the circle rotates θ = 2 π r P ( 3 6 0 ∘ ) (because in the corners there are no rotation of the circle around the centre A ) where P is the perimeter of the pentagon.
Therefore, if we have a regular polygon of n sides, the circle rotates θ = 2 π r 2 R n sin ( n π ) ( 3 6 0 ∘ ) where R is the circumradius of the regular polygon. When n → ∞ , we have n → ∞ lim n sin ( n π ) = π .
So θ = 2 π r 2 R π ( 3 6 0 ∘ ) = r R ( 3 6 0 ∘ ) , in particular, if r = 4 R we have θ = 4 ( 3 6 0 ∘ ) (i.e. the value is 4 ).
Log in to reply
@Zuriel Aquino – Thanks. I've edited the problem for clarity, to indicate that we want the rotation about the center of the small circle, as opposed to the rotation with respect to the large circle.
You are right to bring up the 2 types of actions that cause rotation
1. The circle has to roll along the perimeter
2. The circle has to rotate around a corner
The first action results in 4 rotations (analogously, but not perfectly, moving along a line of length 8 π r . The second action results in 1 rotation (analogously, but not perfectly, rotating the circle around a fixed point).
Because the big circle has a radius that's four times larger than the small circle, its circumference is four times as big.
Imagine that the big circle is a piece of string.
Cut the string at the point where it touches the small circle and pull the string out into a straight horizontal line, with one point still touching the small circle.
Now roll the small circle along the straight piece of string.
It will have rotated exactly four times by the time it reaches the end.
Now return the string to its circular configuration and roll the small circle along the string.
The small circle will again rotate four times because it's touching the string, and one extra time because the string goes around in a circle.
Hence the answer is five.
CORRECT!!!
Log in to reply
But we are interested in the diameter, not the radius. So we multiplied by 8 to get the horizontal diameter. We had another 8 to get the vertical one. 8 + 8 = 16. 16 divided by 4 is 4 !!
The answer is 4 you guys.
Let me prove it: Take 2 coins of equal size. Have one coin rotate around the other, but before doing so, mark its starting point with a pen. Now notice that the coin takes exactly one revolution before reaching the marked point. This is because the circumferences are equal. Mathematically, there should be no need to add 1 to your answer. If a circumference of the larger circle is 4 times greater, there should be a total of 4 revolutions.
Log in to reply
I totally understand why you don't think you need to add the extra revolution. It didn't make any sense to me either for a long time. There's one thing to notice that might help you see where everyone else is coming from. Let's say you start with two coins of equal size and you start with the moving coin right-side up, so that the bottom of the coin is touching the fixed coin. After going halfway around the coin, the top of the moving coin will be touching the fixed coin. This makes sense, we moved half of the circumference and now the opposite side of the coin is touching. The trick is that the moving coin is now at the bottom of the fixed coin, so if the top of the coin is touching, it means that the coin is now right-side-up again. The coin is now in the same orientation as wen it started, which means that it must have undergone one full revolution after going halfway around the circle. It's completely ridiculous sounding at first, but if you try it for real you'll see that the coin will in fact make two whole revolutions when it goes around the other coin.
Nope ..think of a sphere pure rolling on a rough track.. now for a rotation of 2π radians i.e one rotation its centre actually translates 2πr units or one could say for nπr units travelled by centre of sphere no. of rotation is n ..in the question the centre of small sphere covers 5πr units on the bigger sphere so no. of rotations are 5
I never actually figured out the solution, I just remembered a previous video by MindYourDecisions that pretty much had the same problem and solution, you should really check it out. Here is the link https://www.youtube.com/watch?v=kN3AOMrnEUs
believe in the heart of the cards
Imagine that the two circles are gears with fixed centers. When the large circle rotates once, the small circle will rotate four times. Now, repeat the experiment, but rotate your head with the large gear, so that it appears to stand still. The small circle will still rotate four times, but will appear to rotate five times since your head rotated once. This view is exactly equivalent to the question, so the answer is five.
Thank you, your answer makes the most intuitive sense, an even simpler analogy, is draw a smiley face and place a dot in between it's brows and rotate it through one full revolution and it takes 5 rotation to be at it's original position.
The answer would have been 4 if the smaller circle was rolling along with the interior of the larger circle. Its path would trace a ring of width equal to the radius of the smaller circle. This ring is contained within the larger circle and so the smaller circle is traveling a path equal to the circumference of the larger circle.
However, for this problem, the smaller circle is rolling along with the exterior of the larger circle. This might appear no different from the case discussed earlier but the smaller circle is actually tracing a ring of width equal to its own radius on the outside of the larger circle. This means it is actually covering a distance equal to the sum of the circumferences of the smaller and larger circle!
And so this tricky problem that got many people turns out to have an answer of 5 since the radius of the larger circle is 4 times that of the smaller circle.
The tricky part about this problem is there is an imaginary circle of radius equal to the sum of the radii of the smaller and larger circle which is being hugged by the smaller circle as it rotates. The circumference of this "hidden" circle is actually what is being travelled by the smaller circle as it rolls along the outside.
Let A be the point of the small circle that touches the large one. It begins the movement "facing down".
When the small circle is placed right to the large, point A will be again in contact with the large circle, but this time it will e "facing left", which means an additional 90º rotation (or 1/4 of a revolution).
Therefore, when the smaller circle gets back on top of the larger, point A would have rotated 4 x (1 + 1/4) = 5 times.