This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
(-2)^2=4 so there are 2 solutions. It's the basic
Log in to reply
The square root function is defined to give the positive square root as a result. See this for more information.
Log in to reply
@Abdur Rehman Zahid I guess the definition should be presented first, as in .... "IF the square root function is defined as...." since clearly a significant segment of the math population appears to have different definitions, would you not agree? You link merely re-iterates in depth, IMO
Square root is defined for only one thing the reverse of square function not to give the positive or negative result. over range of integers it is many to one function, i mean it does'nt matter number is positive or negative or imaginary. squareroot is just reverse of squre function. Atleast that's what i learn.
This is incorrect, and the link that you shared is a different example. If this were to say the square root of a square, then the value would in fact only be positive. However, application of the operation to a term must include all possible outputs, which would include -2.
Unless the root has an explicit + or - in front of it, you presume both.
Your reasoning and answer are incorrect.
Learn abstract algebra and numerical analysis and you will understand.
Log in to reply
The square root function is defined to give the positive square root as a result. See this for more information.
But the square root of 4 could be either 2 or -2 since both, when squared, equal 4
Log in to reply
The square root function is defined to give the positive square root as a result. See this for more information.
Unless stated, the square root symbol without any negation signs suggests both values are solutions.
Log in to reply
No it doesn't.The square root function is defined to give the positive square root as a result. See this for more information.
This is absurd. I am reading all of these comments and I can't help but agree with one of you, Thomas. He stated that having a clear/specific question is very important! Inputting values into the sqrt function will always yeild positive numbers on output. Yet last I checked that's not the question. Had the question been "What would the graphical or computer process yeil from the following operation:..." then I would agree that the obvious answer is 2. However, since nothing was stated in the question, an abstract question deserves an abstract answer.
If you are stating that sqrt() is a function that returns only the principal square root value, you should better state that in the quizs. I've just landed here thinking no tricks are supposed to apply and then I get this.
That's wrong buddy. If you take the square root of something, you're reversing the square operation. So, look at it this way: if you take the square root of 4, the reverse of that could be 2 or -2 because 2^2=4 and -2^2=4. There is no absolute value sign involved.
Log in to reply
Hi Casey, that's not true. The square root function does not reverse the square operation. That might have been the way that you were first introduced to it, as a simplistic way of understanding it. However, the square root Functions only returns the positive root.
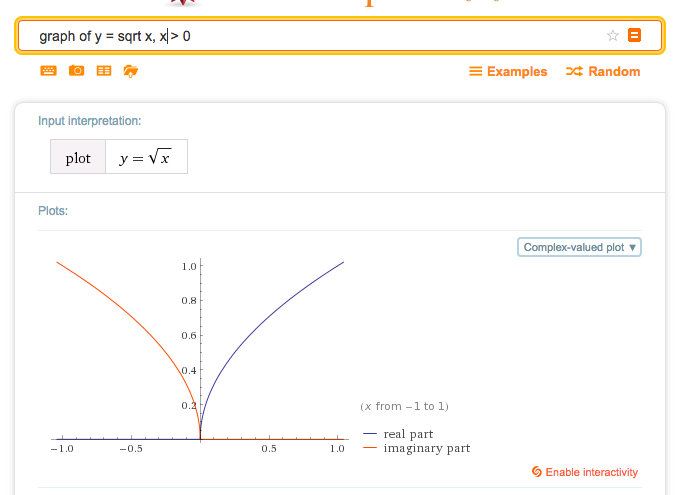
For example, if we consider the graph y = x , we do not include the point ( 4 , − 2 ) .
c.f. Wolfram Alpha
You cannot use an article on YOUR website to justify a wrong answer on YOUR quizzes. At least post a reference to an external authority, I mean even Wikipedia would be better! https://en.wikipedia.org/wiki/Square_root
You needed to have been more clear. In the definition you linked to, it talks about taking the sqrt operation, as in its graph form, just covering the non negative real x axis, however you can not do this unless you are stating that, simply because it is a operation and doesnt always have to be a defined function. By that i mean, you are taking values from a domain, imputing them and then obtaining their values after being operated. The domain is non negative real numbers but the range is real numbers. For it to be a defined function however you then can only take the non negative real numbers, because you need to make it 1 to 1, so you take out all the negative answers. Im not moaning, just saying clarety helps :)
But (-2)² =4 and also 2²=4.
in russian maths sqrt is a function that gives to answers. so if you have an equation x=sqrt4 the answer would be x1=2; x2=-2
The comments in support of 2 as the only solution are focused on the square root defined as a function. The comments in support of the {2, -2} solution are focused on the square root defined as an inverse operation. The question simply uses the square root sign, which could be interpreted as either the function or the inverse operation.
If you wish to arbitrarily redefine the square root function as mono valued or only including its "principal" solution then you are correct, however maths is a universally agreed set of conventions which facilitate understanding and computation (eg the solution of problems which can be expressed in terms of quadratic equations). To this end we accept that there are two roots (whether 2 real. one repeated or two complex) of any quadratic equation. To deny this is to undermine the credibility of this entire website.
You have to define first if the solution has to be in natural or integer numbers first
What about the proof for the quadratic formula. This is not complete unless you consider the positive and negative solutions when you calculate the square root?
This wrong - the answer is either 2 or (-2) - the square root function does not return only the positive square root.
but (-2)*(-2)=4 too
It is just flimsy semantics to say that the sqrt. function returns ONLY the "Principle square root"
-22 is also4
Hey hey hey!!! Why all the 'not needed' disrespect, negativity and proving the point? There must be an explanation from the one who has created the question, serving as a reference, SAVING all others' time and energy (thoughts).
This is not mathematics... it is POLITICS as it is a CONVENTION only!!
Why does the Riemann surface for the square function have TWO branches (surfaces) then? Because the INVERSE operation (the root) has two solutions!
Hello everyone! The correct answer is... Well both only 2 and x1= 2, x2 =-2. When I tried the quiz I inputed 2 and -2, because I expected the Domain of "4" was R (The real numbers ) but it was not specified, so both "2 and -2" and "2" should have been correct answers. In fact the question should have specified that 4 belongs to N (the natural numbers ) to say that the answer was "2" . The docs related to article, if refered to the domain R, are incorrect .
Cheers
By the way, I study engineering, so if I had ever written something like 4^(1/2) = 2 without specifing any Domain, I would have pissed a lot of professors! Even the ones not strictly related to Math. Simply beacuse we live in a world where Complex numbers rule (A super set of R )
I was also confused about the answer because I was always taught that the square root of a number has two answers, but let's be honest...nobody really solves square roots that way. In practice we always only return the positive answer. A good example is Pythagorean's Theorem for finding the hypotenuse of a right triangle. I've never heard anyone try to claim that the hypotenuse could have a positive or negative length just because it's the result of a square root.
Funny the section is called "common misconceptions" and starts with one of them, i.e. assuming that "if I don't tell you anything, my square root results are always positive" . Plus, uses a self-written article to support his/her nonsense... OMG!
Wow this is such blindness. Are you out to change convention or just make people dumber? Revenge on your teachers for telling you something you didn't agree with?
I went back and forth between whether it was 2 or -2, or 2 and -2. I was taught that the root of a square had both negative and positive answers. Though it seems counter-intuitive at first, I accepted it. Is it a calculator thing? I mean, I don't know how calculators are programmed these days (I used to), but why is the negative answer ignored or discounted? No such thing as negative space? If so, why was it taught to me this way?
It can be 2 values right?
It is not complaining, it is just a basic thing in algebra and computing in general, that square root of positive real number has got two results, one positive and another negative. For instance, we can see this also as follows : sqrt((-2)^2)=-2
Oleg Yovanovich
guys...
think about it this way.
how many solutions does x^2=4 have?
2 and -2 obviously.
but THAT DOES NOT mean that sqrt4=x has the same solutions.
take x/x=1 for example. sure, you would say that all x work, but 0 doesn't. same here. you can't square both side sof sqrt4=x and say that the roots are the same, just like you cant say x=x in x/x=1 so all reals, because there are extraneous roots, or -2.
Note:
Ever heard of sines and cosines? The principal value is the 'default' value, which in this case is positive (principal value is positive), which is why it's called the principal root.
So, it's 2.
really the instant i looked at this i KNEW, just KNEW, it would start an argument.
Stop complaining, people The answer is correct, a squareroot never has a negative answer.
Log in to reply
The answer is not correct, correct answe would be |2|, apsolute of 2 meaning -2 and 2.
(-2)x(-2) = 4 (2)x(2) = 4 sqrt(4) = +2 OR -2
Log in to reply
no,square root of a positive number will be only positive.
Log in to reply
you idiots negative 2 times negative 2 equals positive 4
Log in to reply
@Manlai Battulga – it seems you are very talented,bro.then, explain the thing what you actually wanted to tell?
You're confusing a square of a (non complex) number will always be positive. Not the square ROOT. Taking the square of a negative number results in a complex number. Take the square root of a positive number results in two solutions.
That being said, the root notation per this problem should return the principal square root, which is the positive value of two solutions.
sore loser mad that u missed it
a square root is always positive
2 and -2 are different values. Since 2^2 = 4. And -2^-2≠4. -2 isn’t squareroot of 4
Note that ⋅ is a function that returns the principal square root; here, since 2 2 = 4 , 4 = 2 .
To read more about why there are not two values, see does a square root have two values?