A classical mechanics problem by A Former Brilliant Member
A uniform cylinder of radius is spun about its axis to an angular velocity and then placed in a corner. The coefficient of friction between the wall (and floor) and the cylinder is . How many radians does it spin through before stopping?
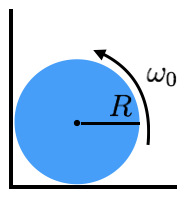
Assumptions and Details
The answer is 0.0665.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Given:
→ μ = 3 → ω 0 = 2 π → R = 0 . 2 5 m → g = 1 0 m s − 2
Let m be the mass of the cylinder, F 1 be the frictional force acting along the floor and F 2 be the force acting along the wall as shown in the following figure.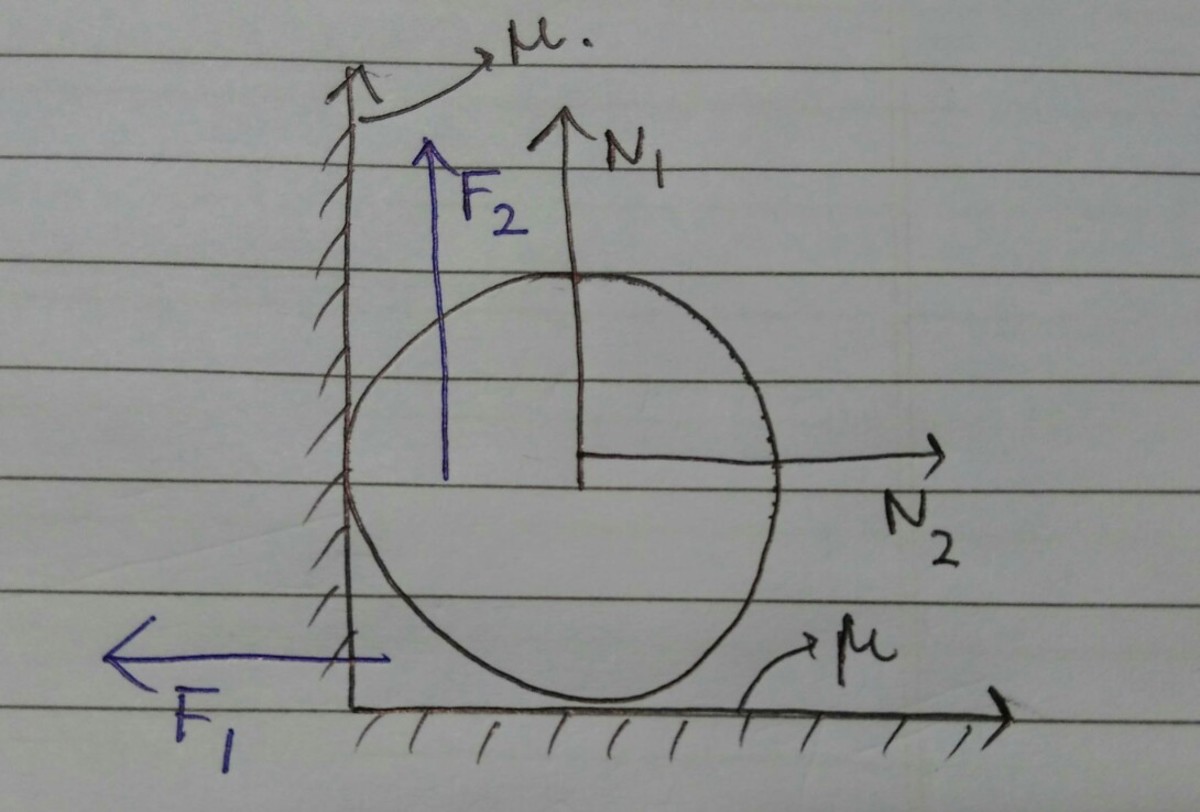 Equating components of force and normal reaction horizontally and vertically and using the laws of friction we get:
N
1
+
F
2
−
m
g
=
0
⋯
(
1
)
F
1
−
N
2
=
0
⋯
(
2
)
F
1
=
μ
N
1
⋯
(
3
)
F
2
=
μ
N
2
⋯
(
4
)
Using (1), (2), (3) and (4) we get:
F
1
=
1
+
μ
2
μ
m
g
and
F
2
=
1
+
μ
2
μ
2
m
g
Moment of inertia, I is equal to
I
=
2
m
R
2
Net torque acting on the cylinder
τ
n
e
t
is
(
α
is the angular acceleration):
τ
n
e
t
=
−
F
1
R
−
F
2
R
=
I
α
⇒
I
α
=
μ
m
g
1
+
μ
2
1
+
μ
⇒
α
=
R
(
1
+
μ
2
)
−
2
μ
g
(
1
+
μ
)
α
and
τ
n
e
t
are with a negative sign because the direction of
ω
0
was assumed to be positive and the
τ
n
e
t
and
α
acting are opposing it.
Equating components of force and normal reaction horizontally and vertically and using the laws of friction we get:
N
1
+
F
2
−
m
g
=
0
⋯
(
1
)
F
1
−
N
2
=
0
⋯
(
2
)
F
1
=
μ
N
1
⋯
(
3
)
F
2
=
μ
N
2
⋯
(
4
)
Using (1), (2), (3) and (4) we get:
F
1
=
1
+
μ
2
μ
m
g
and
F
2
=
1
+
μ
2
μ
2
m
g
Moment of inertia, I is equal to
I
=
2
m
R
2
Net torque acting on the cylinder
τ
n
e
t
is
(
α
is the angular acceleration):
τ
n
e
t
=
−
F
1
R
−
F
2
R
=
I
α
⇒
I
α
=
μ
m
g
1
+
μ
2
1
+
μ
⇒
α
=
R
(
1
+
μ
2
)
−
2
μ
g
(
1
+
μ
)
α
and
τ
n
e
t
are with a negative sign because the direction of
ω
0
was assumed to be positive and the
τ
n
e
t
and
α
acting are opposing it.
Now, when the circular motion of the cylinder stops, ω t 2 = 0 = ω 0 2 + 2 α θ ⇒ θ = 4 μ g ( 1 + μ ) ω 0 2 ( 1 + μ 2 ) R = 4 × 1 0 ( 3 + ( 3 ) 2 ) 4 π × ( 1 + ( 3 ) 2 ) × 0 . 2 5 ⇒ θ = 0 . 0 6 6 3 9 rad ≈ 0 . 0 6 6 5 rad