It's not like the others
∫ 0 ∞ x 2 3 + x 2 2 + x 2 1 + … + x 2 + x + 1 x 2 1 + x 2 0 + x 1 9 + … + x 2 + x + 1 d x
Given that the integral above equals to A π ( B 1 + C 1 + D 1 + E 1 ) for positive integers A , B , C , D and E .
Find the minimum value of B × C × D × E ÷ A .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Pi Han Goh I hope that's a fine solution(non-English). Another use of the Master! I'm lovin it.
Log in to reply

Even I used the same method. R u really 15, cuz ur solution make me think u r a phd at maths
Log in to reply
Of course I am 15. But if my solution make you think I am a PhD at Maths, then I'd think the same for you as you also used the same method and are less than an year older than me.
Log in to reply
@Kartik Sharma – Actually I'm going to be 17 next moth. I've seen many of ur solutions. They r really amazing!
Log in to reply
@Aditya Kumar – Oh, thanks. BTW, I'm also going to be 16 next month.
You're really good at Mechanics and EM as I have seen. Just amazing.
Log in to reply
@Kartik Sharma – Haha thanks! Btw maths is the mother of all.
One can find the general integral of such form in the same way. I will give the generalized form also.
Log in to reply
POST POST POST!!!
Log in to reply
Just the generalized form -
∫ 0 ∞ 1 − x b 1 − x a d x = a π ( s i n ( a π ) e π ι / a − s i n ( ( b + 1 ) a π ) e b π ι / a )
Proceeding with the constants a , b like I did in the problem generalizes it.
where did you learn Euler's reflection formula and the other 2 fancy theorems?
Log in to reply
You don't actually need to apply all these fancy theorems, see my solution given in "inspiration".
Euler's reflection formula pops up very often for gamma functions so it's useful to know it.
how to get cot 2 4 π = 2 + 2 + 3 + 6 ?
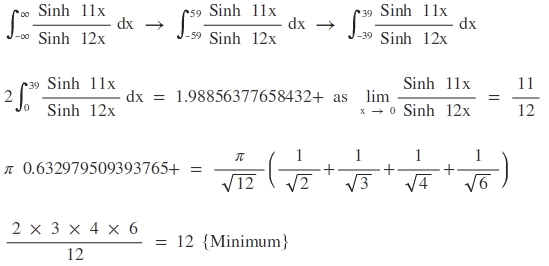
I suspected this as a wrong direction however I know that I can solve via numerical method.
I have just updated upon request.
∫ 0 ∞ 1 − x 2 4 1 − x 2 2 d x
∫ 0 ∞ 1 − x 2 4 1 d x − ∫ 0 ∞ 1 − x 2 4 x 2 2 d x
I 1 = ∫ 0 ∞ 1 − x 2 4 1 d x , I 2 = ∫ 0 ∞ 1 − x 2 4 x 2 2 d x
I 1 : x 2 4 → x
2 4 1 ∫ 0 ∞ 1 − x x − 2 3 / 2 4 d x
2 4 1 M ( 1 − x 1 ) ( 2 4 1 )
M ( f ) ( s ) - Mellin transform of f at s
Using Ramanujan Master Theorem,
2 4 1 Γ ( 2 4 1 ) Γ ( 1 − 2 4 1 ) ( − 1 ) 1 / 2 4
Using Euler's Reflection Formula,
2 4 1 s i n ( 2 4 π ) π e π ι / 2 4
I 2 : x 2 4 → x
2 4 1 ∫ 0 ∞ 1 − x x − 1 / 2 4 d x
2 4 1 M ( 1 − x 1 ) ( 2 4 2 3 )
Proceeding as before,
2 4 1 s i n ( 2 4 2 3 π ) π e 2 3 π ι / 2 4
Putting them in one,
2 4 s i n ( 2 4 π ) π ( e π ι / 2 4 + e − π ι / 2 4 )
1 2 π c o t ( 2 4 π )
1 2 π ( 2 + 6 + 3 + 2 )
1 2 π ( 3 1 + 2 1 + 4 1 + 6 1 )