It’s scandalous!
If two point charges + q and − q are separated by distance d , then according to Coulomb's law , the attractive force between them is
F e = k e d 2 q 2 ,
where k e is Coulomb's constant. But what if the charges were distributed on spheres instead of at points? Two charged conducting spheres with charges + q and − q are separated by center-to-center distance d .
The attractive force between them is __________ .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Wait... you are completely right, but it never said that they were uniformly divided in the sphere. They could be at the farthest point of each sphere
Log in to reply
If the charges were uniformly distributed in the spheres, or on their surfaces, or in any spherically symmetric way, then the attractive forces would be equal to the situation of two point charges.
However , since the spheres are conductors, the charges move until equilibrium is established. At this equilibrium, the charges are on the side of each sphere that is closest to the other sphere; the charges are now closer together, so the force is now greater.
Log in to reply
The question doesn't mention equilibrium. Or allowing the charges to move. If the charges can move, can d change too?
Log in to reply
@Richard Desper – "Conducting" gives information about what the charges may do. Typically, the equilibrium of charges on conductors is established very quickly, while the mechanical effects are much slower.
@Richard Desper – You might find the doc I referred useful. Go check it out!
This might helpL www.physics.princeton.edu/~mcdonald/examples/perfect.pdf REFER TO 2.1.7
You many wanna verify in lab.
If the distance, d, between the spheres is sufficiently large, then the electric field of one sphere will be negligible at the location of the other one and the charge will be uniformly distributed on the surface. In this case, the two spheres will look like point charges.
'Greater than ke.q2/d2' only applies when d is small. When d is large compared to the diameter of the spheres the force tends to 'Equal to ke.q2/d2'.
Log in to reply
That is an approximation which we assume to be true for all practical purposes. However the force is never exactly equal. Even when d is very large, the force is ever so slightly greater in the case of conducting spheres compared to point charges.
The force of attraction is dependent upon the distance between the two charges. Placing a sphere between the two charges does in no way change this distance. (I am assuming that the sphere is merely a spacer and in no way can change the magnitude of the force between the two charges). Once the two charges are on the sphere, then and only then can they move thus the answer is wrong and the equation will still hold true.
WRONG. the question specifies the charges are "distributed." So the answer is "equal to..."
Relevant wiki: Conductors
If the sphere is a conductor the charge will focus more on the inner sides being attracted by the other sphere, and the force will increase
EDITED: I originally believed that 2 uniformly charged spheres will have a bigger force, but this is not true. In this case the force is exactly the same. Original flawed argument, please ignore because it's not that simple: I believed that even if the charge is uniformly distributed on the sphere, the increased attractive contribution of the closest sides is stronger than the weakened attractive contribution on the far sides, due to the dependency on the distance as d 2 1 , because ( d − r ) 2 d q − d 2 d q > d 2 d q − ( d + r ) 2 d q
Being additive, as long as the charge can't move, the force will be equal since a given point on a sphere will still be an equal distance from the same point on the other sphere. However, if the charge distribution can move, it'll attract inwards further strengthening the force.
Log in to reply
The force will not be equal as the denominator is d^2
If the charges were uniformly distributed, the increased attractive contribution of the closest side is actually equal to the weakened attractive contribution on the far side! What you forget to take into account is the increased distances in the direction perpendicular to the connecting axis.
Log in to reply
The problem states point charges +q and -q. Using a lower case q implies a single charge such as an electron or proton. If the electron and proton can move about the sphere then the analysis of the force being greater then Kqq/r2 is correct. However if the charges happen to be an electron and proton, then the force is equal to Kqq/r2. This is the way I read the problem
Log in to reply
A "point charge" does not necessarily mean a specific elementary particle. It simply means that charge is distributed so closely that, for all practical purposes, it may be considered as residing at one point. (Note that even a proton on closer inspection is not a point charge, but a finite-sized charge distribution.)
The problem then continues to say that the charges are "distributed", which implies precisely that it is no longer at one place but spread out over space. The expression "the charge q is distributed" is short for saying that there is a charge density ρ on the given support V , such that q = ∫ V ρ d V . I like the short way of saying :)
The denominator is d^2 so the effect is not linear
Log in to reply
The question is not if the effect is linear, but do they somehow cancel in the case of uniform distribution.
Thank you, you're probably right. I couldn't find a proof of it though. I've tried http://www.wolframalpha.com/widgets/view.jsp?id=6a68b5e97b4f834f58e777a4dceaed0 and typing "1/((cos(theta) cos(phi)-10)^2+(sin(theta) cos(phi))^2+(sin(phi))^2)" the value seems quite close 4*PI()/10^2
This could be a calculation approximation though
Log in to reply
It seems to me that the proof is the same as for the gravitational field due to a sphere which is uniform. You need calculus but any elementary physics book with calculus has the proof.
Log in to reply
@Donald Yasnyi – Indeed, it is simply another application of Gauss' Law.
@Donald Yasnyi – Thank you, yes, similarly it makes sense that the force on a charged particle inside the charged sphere shell is 0. http://hyperphysics.phy-astr.gsu.edu/hbase/Mechanics/sphshell2.html So it makes some sense that even if the point is outside there are no extra contributions. I'm going to update my solution
The problem stated "CONDUCTING spheres," so how could the charges remain "uniformly distributed" once each is under the influence of the oppositely-charged sphere? Once the fact that the conducting spheres will polarize under each other's influence (I'm embarrassed to have missed it initially) is recognized, the answer is obvious.Or am I missing something (my elementary field theory has barely been consulted in 50 years)?
Log in to reply
The one slightly valid complaint could be that the charges may not have reached equilibrium yet.
nowhere in this problem do i see the words "uniformly distributed"
It does not become uniformly distributed. Charges on a conductor will distribute themselves quickly to a situation of equilibrium. On an isolated conducting sphere, there will be a uniform distribution on the surface; in this case, the equilibrium charge density will be highest at the surface near the other sphere, and least on the opposite side.
If the charge distribution were uniformly distributed, the force would be the same as in the case of the point charges. But with the polarized equilibrium distribution, the force is greater.
Look at the case when only one of the objects has charge. For point charges the force is zero. For conducting spheres there is an attraction, because of the polarization of the non-charged sphere. That extra attractive force is also there when both objects are charged (in fact, it will be twice as much, if the charges are equal and opposite).
Why is there polarization on non-charged sphere conducting spheres if considering there is no voltage potential E on the conducting object?
Log in to reply
There is a potential - from the electric field due to the charged sphere. :-)
Log in to reply
Assume the conducting volume resistance R is 0, if there is potential E building up, the current I = E/R will be infinity. That seems impossible.
According to Faraday shield, the voltage potential cannot build up on a conducting object.
Log in to reply
Indeed, the electric potential is the same all over the metal. It does not follow that there is no re-distribution of charges. In fact, exactly the opposite: if there is no redistribution, the potential would not be the same.
Let us say that the point charge is negatively charged. When you bring the point charge close to the sphere, the electrons on the sphere will move under the influence of the electric field created by the point charge. Due to the repulsion, the electrons that are on the hemisphere that is closer to the point charge will move to the other hemisphere (roughly speaking) until a new equilibrium is reached. In this new equilibrium the surface of the sphere is an equipotential surface, but one half of the sphere is positively charged and the other half is negative. This is called "polarization" or "induced charge distribution". Since the positively charged half is closer to the point charge than the negatively charged one, there will be a net attraction.
Log in to reply
I am not sure I understand the “induced charge distribution” on conducting metal under the electric field. If that is true, I can use a wire connecting to one end of a metal bar, which is under strong electric field, and another wire connecting to other end of the metal bar. This will become an endless power source. But this won’t happen in real.
 electric field power source
electric field power source
Log in to reply
@Jingxi Zhang – In your example, there will be a similar induced charge distribution in the wires leading to the motor, acting against the charge distribution induced in the metal bar. There will be no current flow.
In you drawing this is not apparent, since you did not indicate the electric field in the lower part of the picture. It is the beauty of the Maxwell equations (the equations that describe the behavior of electric and magnetic fields) that the electric filed cannot be suddenly zero as you move from the top of the picture to the bottom, and the overall effect of the field on the wire will be exactly as I described above.
For people who want a simpler and easier to understand solution: d is the distance between the CENTERS of two spheres which makes the attractive force greater because the charge doesn't stay in the centers of the spheres, it's on the surface which makes the actual distance between charges smaller than d and as we see on the formula, the force gets greater the smaller the distance becomes.
Awa thanks
Simpler rapid answer this is how our planetary universe functions.
In presence of oppositely charged sphere, the attraction causes polarization. On each sphere the charge will collect at the surface closest to the other charges, thus minimizing the electric energy between the spheres. The attraction forces between all point charges on the sphere will be maximum. Here, along with that, as same charges come closer, the repulsive might go to a peak as between them distance decreases. So let's look at this mathematically.
Suppose you don't know what conductors are,
But you assume initially that you kept the spheres with a uniform distribution of charges two of opposite charges kept at a distance d, instantaneously, the force acting can be compared mathematically.
There are only 3 possibilities where the distance between charges will be very less than or equal to that of distance between 2 point charges. As force is inversely proportional to the distance, it can be maximum or equal in these three points. At other points in both spheres, as the distance is varied or too large, or always greater than the shortest distance (middle line), they can be neglected at first.
Let's assume at first that the force between the 2 point charges is equal to that of the cumulative forces of the 3 distant charges as shown.
As the charge is uniformly distributed on the surface, assume M is the charge per unit area.

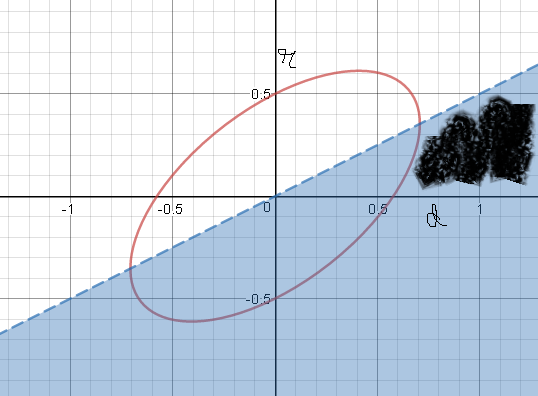
Then d >> 1 + 2r, should be a necessary condition, with suitable units. Assuming that condition would suggest that along the points, in the region marked in the graph, the force will always be greater. If inside, it would be smaller.
But, we neglected the other forces before, considering these small forces we can assume that it will be, even if little, greater than that between point charges. Thus the answer that its always greater is partially correct. The force depends largely on the radius.
But!, if point charges are assumed as spheres of radius r < 1 approx, and bigger spheres r > 1 approx, the force will be of course greater between the latter.
I don't know if this makes sense for you, but I got so happy when I finally got an intermediate question correct, so I just wanted to post how I got it:
I honestly didn’t really understand the question first, so I broke it into small sections and tried to understand it. I thought it has to be something with a force pulling the two spheres together or from each other. The force between +q and -q as points is
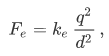
And the question is telling me to figure out if the force is bigger, smaller, or the same when those two points turn into spheres. I thought the attractive force is bigger now, because for example in space, bigger planets have bigger gravitational force. So I think that in scenario, bigger points have bigger attractive force. Which was correct!
In question they have only mentioned attractive force . So we can think that since point charges are turned in spheres , the gravitational force would also increase which results in increase in net attractive force.
Even if you just consider the electrostatic forces, they are greater in the second case where there are conducting spheres instead of point charges.
The sphere as a whole is charged, therefore a. the charges +q and -q have increased. b. the distance between charged points has decreased
Hence, the attractive force increases.
Why would charge increase?
The problem doesn't say: "the charges were induced to the conductors(already charged) "; however, it does states the conductors were neutral before inducing.(implicit)
You're violating law of conservation of many ABC's; charge stays constant; polarization tricked you.
Relevant wiki: Conductors
The intuition comes from reading the initials of your book/repeating in the lab. That'll be imminent for the setup to reach in equilibrium, so you may want to use a graphing tool to record how the charges behave initially( opposites rush to the other shell ).
Common misconception: Uniformly distributed? No! It's not. It'll be imminent but not immediate. Hope this helped.
By the first case there are only two charged particles. But , by the second case there are no. of charged paticles. And as we know greater particles will attract with greater force than less particles. Therefore , answer is greater than kq^2/d^2.
The charges are opposite and attract and will migrate to the points opposite each other on each sphere. Then the distance,d, between the charges is smaller and d^2 is larger therefore the force, Fe, is greater. However I think the choice of answers may have to reworded to say something like the attractive force Fe is greater OR the value of ke(q^2/d^2) increases. As it is it seems to read the attractive force viz ke(q^2/d^2) is greater than ke(q^2/d^2). Which is not quite right, I think.
As you have shown, the distance between the "effective" charges is less than d , so the attractive force in the case of conducting spheres is greater than k e d 2 q 2 . Here d is a constant referring to the distance between the point charges. If the new distance is d ′ < d , then the new attractive force is k e ( d ′ ) 2 q 2 > k e d 2 q 2 .
Relevant wiki: Conductors
If the charge were uniformly divided in the spheres, or on the surface of the spheres, then the force would be k q 2 / d 2 by Coulomb's law.
However, the attraction causes polarization: on each sphere the charge will collect at the surface closest to the other charges, thus minimizing the electric energy/field between the spheres. Thus the charges are effectively closer than d , making for a stronger attractive force.