Its time for cubes
Let a 1 , a 2 , … , a 4 denote the roots to the equation x 1 + 2 x 2 + 3 x 3 + 4 x 4 = 0 . Then,
( 8 a 1 3 + 1 ) ( 8 a 2 3 + 1 ) ⋯ ( 8 a 4 3 + 1 ) = − B A
where A , B are positive coprime integers. What is A + B ?
The answer is 51.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Great solution! +1!
Log in to reply
Yes. I cube both sides.
Log in to reply
Thank you! otherwise again great solution!
Log in to reply
@Joel Yip – can this question be done by taking m= 8a1^3 +1 putting values of a in terms of m and then solving .. i tried this but i am not getting the solution please provide i solution in a way i have described...
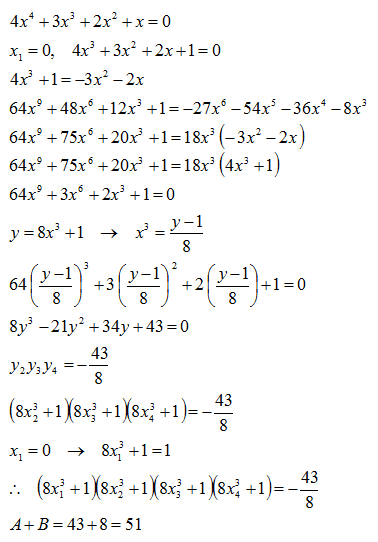
( 8 a 1 3 + 1 ) ( 8 a 2 3 + 1 ) ( 8 a 3 3 + 1 ) ( 8 a 4 3 + 1 ) = 8 4 ( a 1 3 + 8 1 ) ( a 2 3 + 8 1 ) ( a 3 3 + 8 1 ) ( a 4 3 + 8 1 )
With some expansion,
r 3 + 8 1 = ( r + 2 1 ) ( r − 4 1 + 3 i ) ( r − 4 1 − 3 i )
8 4 ( a 1 + 2 1 ) ( a 1 − 4 1 + 3 i ) ( a 1 − 4 1 − 3 i ) ( a 2 + 2 1 ) ( a 2 − 4 1 + 3 i ) ( a 2 − 4 1 − 3 i ) ( a 3 + 2 1 ) ( a 3 − 4 1 + 3 i ) ( a 3 − 4 1 − 3 i ) ( a 4 + 2 1 ) ( a 4 − 4 1 + 3 i ) ( a 4 − 4 1 − 3 i )
In This note , I generalised that type of function and let f ( x ) = ∑ m = 1 4 m x m
We rearrange and 8 4 ( a 1 + 2 1 ) ( a 2 + 2 1 ) ( a 3 + 2 1 ) ( a 4 + 2 1 ) ( a 1 − 4 1 + 3 i ) ( a 2 − 4 1 + 3 i ) ( a 3 − 4 1 + 3 i ) ( a 4 − 4 1 + 3 i ) ( a 1 − 4 1 − 3 i ) ( a 2 − 4 1 − 3 i ) ( a 3 − 4 1 − 3 i ) ( a 4 − 4 1 − 3 i )
8 4 4 ( − 1 ) 4 f ( − 2 1 ) 4 ( − 1 ) 4 f ( 4 1 + 3 i ) 4 ( − 1 ) 4 f ( 4 1 − 3 i )
8 4 4 ( − 8 1 ) 4 ( − 2 1 + 8 3 3 i ) 4 ( − 2 1 + 8 3 3 i ) = 8 4 6 4 ( − 8 1 ) ( 4 1 + 6 4 2 7 ) = 8 4 6 4 ( − 8 1 ) ( 6 4 4 3 ) = − 8 4 8 × 6 4 × 6 4 4 3 = − 8 4 3 = − 2 3 4 3
Thus A = 4 3 and B = 8 . So A + B = 4 3 + 8 = 5 1 .