it's very interesting

$\frac{x}{1-{x}^{2}} + \frac{y}{1-{y}^{2}} + \frac{z}{1-{z}^{2}} = \frac{k.xyz}{(1-{x}^{2})(1-{y}^{2})(1-{z}^{2})}$

$x(1-{y}^{2})(1-{z}^{2}) + y(1-{x}^{2})(1-{z}^{2}) + z(1-{y}^{2})(1-{x}^{2}) = k.xyz$

$x + y + z - xy(x+y) - yz(y+z) - zx(z+x) + xyz(xy+yz + zx) = k.xyz$

Let $x+y+z = S$

$S - xy(S-z) - yz(S-x) - zx(S-y) + xyz = k.xyz$

$S - S(xy + yz + zx) + 4xyz = k.xyz$

$k = \boxed{4}$

$x , y , z \in R$

$x = cotA , y=cotB , z= cotC$

$cotAcotB + cotBcotC + cotAcotC = 1$

$tanC + tanA + tanB = tanAtanBtanC$ ( ------------ 1) ( multiplying both the sides by tanAtanBtanC)

$\frac{tanA + tanB}{1 - tanAtanB} = -tanC$

$tan(A + B) = tan(\pi - C)$

$A + B + C = n\pi + \pi$ ( A triangle exists whenever xy + yz +xz = 1)

$\frac{cotA}{1 - cot^{2}A} + \frac{cotB}{1 - cot^{2}B} + \frac{cotC}{1 - cot^{2}C} = \frac{kcotAcotBcotC}{(1 - cot^{2}A)(1 - cot^{2}B)(1 - cot^{2}C)}$

$= - \frac{tanA}{1 - tan^{2}A} - \frac{tanB}{1 - tan^{2}B} - \frac{tanC}{1 - tan^{2}C} = -\frac{ktanAtanBtanC}{(1 - tan^{2}A)(1 - tan^{2}B)(1 - tan^{2}C)}$

$= \frac{2tanA}{1 - tan^{2}A} + \frac{2tanB}{1 - tan^{2}B} + \frac{2tanC}{1 - tan^{2}C} = \frac{\frac{2k}{8}2tanA2tanB2tanC}{(1 - tan^{2}A)(1 - tan^{2}B)(1 - tan^{2}C)}$

$tan2A + tan2B + tan2C = \frac{k}{4}(tan2Atan2Btan2C)$

$tan2A + tan2B + tan2C = (tan2Atan2Btan2C)$ ( as xy + yz + xz =1 (proof similar to 1))

$k=4$

If the identity holds true for any $x,y,z \in \mathbb{R}$ satisfying $xy+yz+xz=1$ , then it must hold true for the particular case in which $x=y=z$ .

The problem becomes then very easy to solve:

$3x^2=1 \implies x=\frac{\sqrt{3}}{3} \implies \dfrac{3\frac{\sqrt{3}}{3}}{1-\frac{1}{3}}=\dfrac{k \cdot \left (\frac{\sqrt{3}}{3} \right )^3}{\left (1-\frac{1}{3}\right)^3} \implies \dfrac{3\sqrt{3}}{2}=\dfrac{k \cdot3\sqrt{3}}{8} \implies \boxed{k=4}$

But no doubt the other posted solutions are much more interesting!

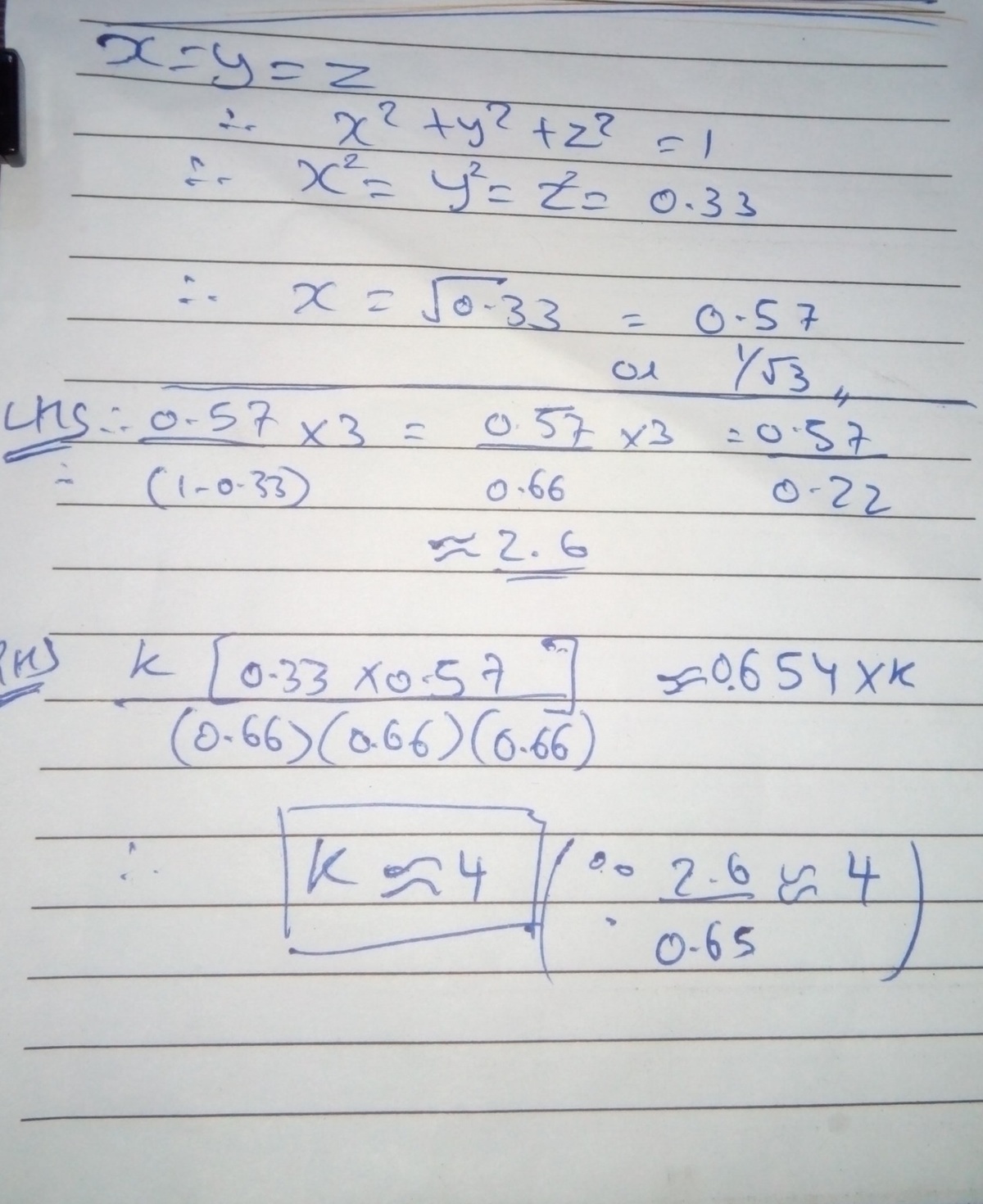dont solve it mathematically, but solve it logically!!