Jagged Line
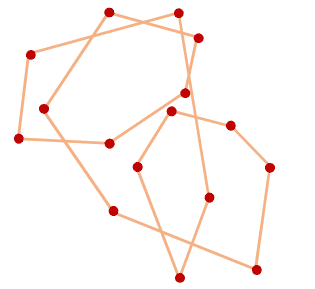
What is the average of all the angles (in degrees) on this line?
Note: Count only angles at the marked points, ignoring the locations where the line crosses itself. At each point pick the "internal" angle, the one that is less than 1 8 0 ∘ .
The answer is 112.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The problem could handle turns in either direction, but one of the directions would need to be designated as negative and the angles in that direction added in as negative numbers.
Log in to reply
Normally we don't do negative angles in geometric drawings, though.
Log in to reply
That is part of the reason I did not set up the problem that way and only mentioned it when you brought up the possibility of such a situation.
Log in to reply
@Marta Reece – I understand. When I post solutions I often state implicit assumptions or observations, to show the limitations of the solution method. It was meant in no way to criticize the problem.
I also noticed that we cannot find the sum of interior angles of certain polygons without additional information. This is one such shape:
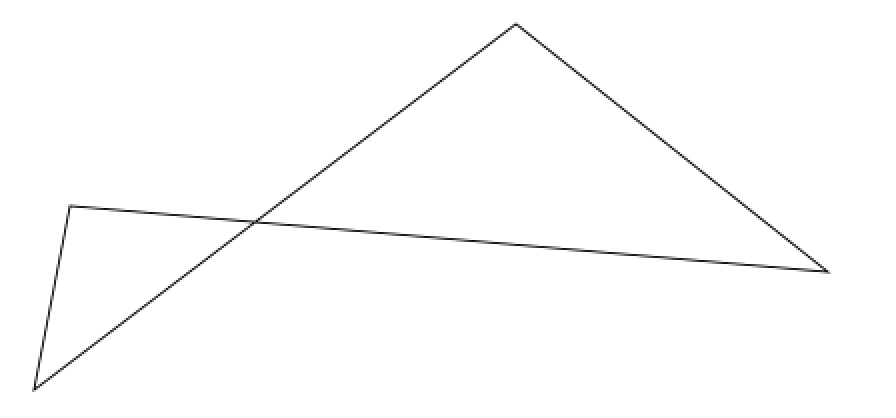
If we use negative angles, then the sum would turn out to be zero, which is not very useful. Is it possible to find the sum of the absolute values of the interior angles of such polygons? I feel it is unlikely because we would require the knowledge of the angle made by the two intersecting lines.
Log in to reply
The problem is that in this case as you cross, the outside becomes the inside and vice versa. So if you roll your rod around on the outside on the left part of the figure, going counter-clockwise, for example. Then you have to continue to roll it on the inside of the part on the right, moving in a clock-wise direction. So you get say 90 and 135 external angles on the left and then add 90 and 45 internal angles on the right. So you get the 360. Then 4x180-360 will give you the figures as expected.
Log in to reply
If we take the quadrilateral with the dashed lines, then the sum would be 360. In this self intersecting quadrilateral, each angle is smaller, so the total would be less than 360. However, we can't say how much smaller than 360.
Awe I counted 15 points... failure
There are 16 points/vertices on the line, and the line winds itself around 3 times, so the answer is
( 1 6 × 1 8 0 ∘ − 3 × 3 6 0 ∘ ) / 1 6 = 1 1 2 . 5 ∘
To see this, let's at every vertex look at both the internal and external angles.
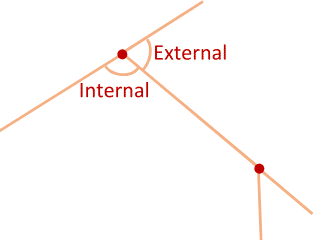
Together the two angles must add up to 1 8 0 ∘ . For the 16 points, this is a total of 1 6 × 1 8 0 ∘ . To get the sum of all the external angles, imagine the top line in the figure above to be a long, straight, rigid rod. Now think of it as rolling around each vertex in turn. At each turn it will rotate by the amount equal to the external angle there. Going all the way around will make that 3 6 0 ∘ . This would be if the curve were a normal polygon. But it is a self-intersecting polygon and it goes around not once, but three times. So the sum of the external angles in all the points is 3 × 3 6 0 ∘ , and this is what we have to subtract to get the total of all the internal angles. Then to get average, we divide by the number of angles.
Great problem and solution! I was under the impression that sum of interior angles of any polygon with n vertices would be 1 8 0 × ( n − 2 ) . Using that value, I got that answer as 1 6 2 5 2 0 = 1 5 7 . 5 . However, this formula only holds true for simple polygons, i.e. polygons that don't intersect with themselves.
I noticed that the sum of interior angles of the polygon in this problem is 1 8 0 0 ∘ , which is the same as the sum of interior angles of a 12 sided simple polygon. Is there a way to transform this self intersecting 16-gon to an equivalent simple 12-gon?
Log in to reply
Actually I solved the problem by converting the 16-gon into a simple 12-gon.
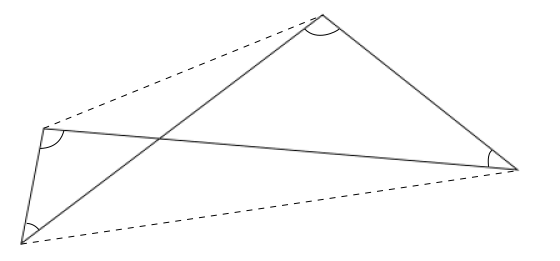
As we walk around, we turn over three full revolutions, i.e. 3 × 3 6 0 ∘ .
Since we make this total turn in 16 steps, the average angle we turn is 1 6 3 × 3 6 0 ∘ = 6 7 2 1 ∘ . The internal angle, on average, is 1 8 0 ∘ − 6 7 2 1 ∘ = 1 1 2 2 1 ∘ .
(Note that this only works because all turns are in the same general direction. If we would have both clockwise and counterclockwise turns, the problem could not be answered.)