JEE maths#14

Let $z = a + bi$ be any complex number. We wish to maximize $|z| = \sqrt{a^2 + b^2}$ subject to the constraint $|z^2 - 9| + |z^2| = 41$ , or:

$|(a+bi)^2 - 9| + |(a+bi)^2| = 41;$

or $|(a^2 - b^2 - 9) + 2abi| + |a^2 - b^2 + 2abi| = 41;$

or $\sqrt{(a^2 - b^2 - 9)^2 + (2ab)^2} + \sqrt{(a^2 - b^2)^2 + (2ab)^2} = 41;$

or $\sqrt{a^4 - 2a^2b^2 + b^2 + 4a^2b^2 - 18(a^2 - b^2) + 81} + \sqrt{a^4 - 2a^2b^2 + b^4 + 4a^2b^2} = 41;$

or $\sqrt{(a^2 + b^2)^2 - 18(a^2 - b^2) + 81} + \sqrt{(a^2 + b^2)^2} = 41;$

or $\sqrt{(a^2 + b^2)^2 - 18(a^2 - b^2) + 81} = 41 - (a^2 + b^2);$

or $(a^2 + b^2)^2 - 18(a^2 - b^2) + 81 = 1681 - 82(a^2 + b^2) + (a^2 + b^2)^2;$

or $64a^2 + 100b^2 = 1600;$

or $\frac{a^2}{25} + \frac{b^2}{16} = 1.$

Hence, our constraint is an ellipse with a semi-major axis length of 5. The maximum modulus of $|z| = \sqrt{a^2 + b^2}$ occurs at either endpoint of the major axis: $(a,b) = (\pm5,0),$ or $|z|_{max} = \boxed{5}.$

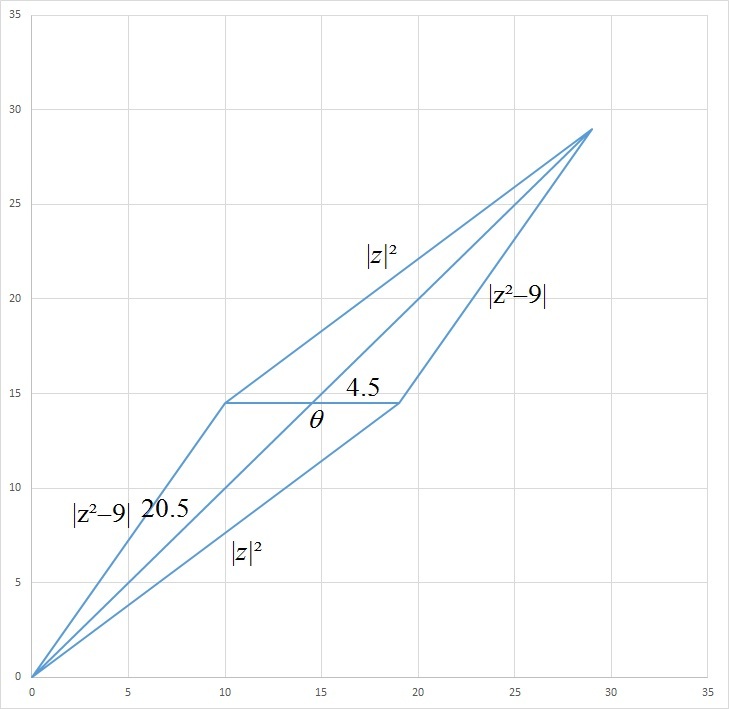
The addition of $|z^2-9|$ and $|z^2|$ forms a parallelogram with the sum 41 being be long diagonal. And $|z^2| = |z|^2$ is maximum when $\theta = 180^\circ$ or $|z|_{max}^2 = \dfrac{41}2 +\dfrac 92 = 20.5+4.5=25$ , $\implies |z|_{max} = \boxed{5}$ .

consider z^2 as Z and thus we now have equation of ellipse in complex form where 2a =41 and centre of ellipse is ( 9/2 ,0 ) so maximum * Z * will be (9/2+41/2,0) i.e. (25,0) but Z is * z^2 * therefore modz=5

note a= semi major axis length of ellipse

I'm not so sure whether we can solve in this way. If any error, please point out. $|z^{2}-9|+|z^2|=41$ $\implies$ $(+-)(z^{2}-9)(+-)z^{2}=41$

Taking the $4$ possible cases of signs, we get the value of $|z|$ as $\dfrac{7}{\sqrt{2}}$ which is $4.95$ approximately $5$

(Someone please help me with latex for writing (plus or minus) above.)