JEE mechanics 1
Masses of 5 Kg and 3 Kg rest on two inclined plane each inclined at 3 0 ° to the horizontal and are connected by a string passing over the common vertex. After two seconds the mass of 5 Kg is removed. How far up (in meters) will the 3 Kg mass continue to move after removing the 5 Kg block?
g = 9 . 8 m / x 2
The answer is 0.6125.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I did it the EXACT SAME WAY
I too did it the same way
Salaam, I have a confusion.... Why didn't the 3 kg block go down? In my opinion, as soon as the 5 kg weight is removed, the only force acting on the 3 kg block is the component of gravity along the wedge (neglecting friction). Kindly share the diagram and/or share a useful link if I'm overlooking some obvious concept.
Log in to reply
Hey, is the question like this? How far will the 3 Kg mass continue to move 2 seconds after removing Kg block?
The 3 kg block did not go down because the force and acceleration caused by the 5 kg block imparts some velocity in the 3 kg block which helps it in moving up, though momentarily because a force starts acting in the opposite direction causing deceleration =D
Log in to reply
TOPPER!!!!!!!!
Log in to reply
@Vaibhav Prasad – Look.. Godfather of toppers is calling a level 3 person a topper.. @Vaibhav Prasad Topper!!!!!!
Log in to reply
@Hrishik Mukherjee – PLEASE DELETE YOUR COMMENT
THE FIRST LINE OF THE QUESTION SAYS THAT THE BLOCKS ARE AT REST. IT SHOULD BE REMOVED TO AVOID CONFUSION COZ LIKE THAT ANSWER IS 0
Hey ! Hey ! Hey ! My ans was also 0.6125 but i typed 0.6.... Sad {LAZY} :(
The gravitational force on both the blocks is gSin30=1/2*g. So the net force pulling 3 up is (5-3)*1/2*g. S o u p a c c 3 = m a s s m o v i n g d u e t o t h i s f o r c e f o r c e = 3 + 5 ( 5 − 3 ) ∗ 1 / 2 ∗ g = 8 1 g . S o u p V 3 , a f t e r 2 s e c = 8 1 g ∗ 2 = 4 1 g m / s . A f t e r 2 s e c , 3 w i l l m o v e u p a n d s t o p a f t e r m o v i n g u p a d i s t a n c e X u n d e r a g r a v i t a t i o n a l a c c . g S i n 3 0 = 2 1 g m / s 2 S o V 3 2 = 2 ∗ 2 1 g ∗ X . ⟹ X = ( 4 1 g ) 2 ∗ g 2 = 1 6 9 . 8 = 0 . 6 1 2 5 .
This question can easily be solved by drawing FBDs.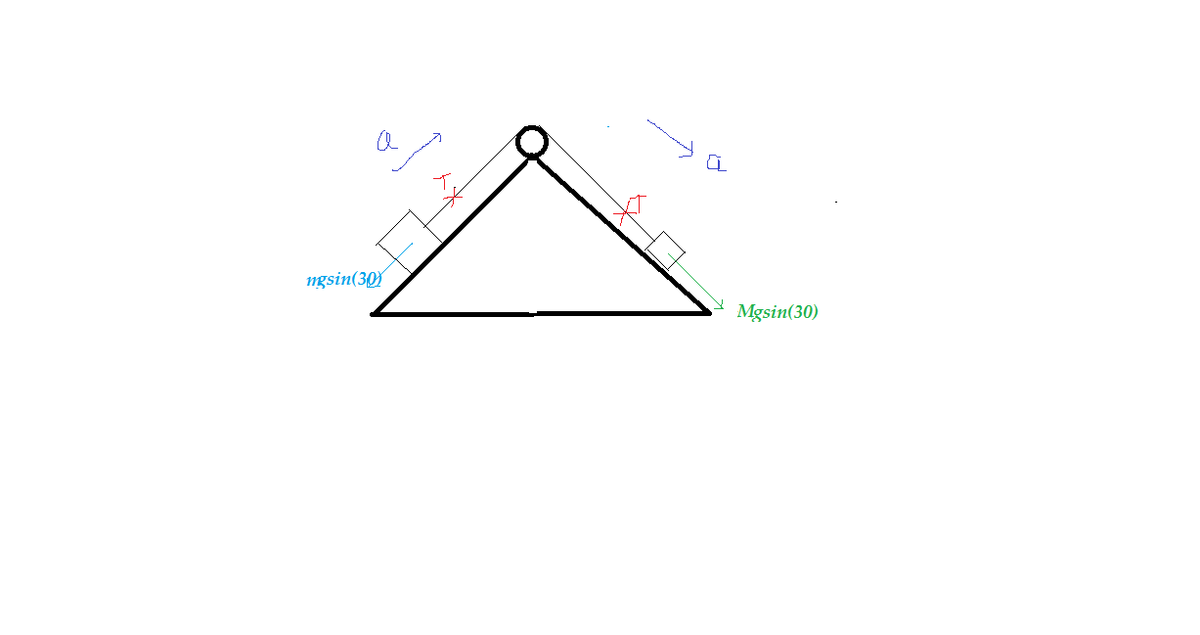 11
11
I have not marked the force acting on the blocks in direction perpendicular to the wedge because they are equal. Also M = 5 k g and m = 3 k g From the figure
M g s i n θ − T = M a .............(1)
and T − m g s i n θ = m a ...................(2)
Acceleration of both the blocks will be same because the string is in extensible.
Adding eq(1) and (2) and then after putting the value we get
a = 4 . 9 / 4
So after 2 seconds the velocity of the 3kg block will be u = 4 . 9 / 2
After the string is cut only a component of gravity acts in the direction acts in the direction parallel to the wedge. So the acceleration of 3kg block after cutting the string is g s i n ( 3 0 ) .
So S = 2 g s i n ( 3 0 ) u 2 Substituting the value we get S = 0 . 6 1 2 5 .